土塞效应对不同壁厚大直径钢管桩竖向承载力的影响

，

(安徽建筑大学土木工程学院，安徽 合肥 230601)

0 引 言

在海洋平台建设中钢管桩基础得到广泛应用。因为钢管桩单桩基础与其他类型的基础型式相比具有承载力大、桩长便于调整、质量能够得到保证、施工速度快以及挤土效应弱对周边影响少等优点。由于钢管桩底部开口，在钢管桩贯入土层的过程中，大量土体会进入钢管桩内部，在钢管桩内形成土塞。而由于钢管桩内部存在大体积的土塞，使得大直径钢管桩承载特性变得较为复杂。所以需要在考虑土塞效应的情况下，通过改变各项控制因素来探索其对钢管桩基础承载力的影响。文章通过ANSYS有限元软件，分析钢管桩不同壁厚对其承载力的影响。

1 理论分析

根据《建筑桩基技术规范》(JGJ94-2008)中钢管桩单桩竖向极限承载力公式：

Quk=Qsk+Qpk=u∑qsikli+λpqpkAp[4](1)

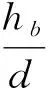
(2)

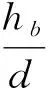
(3)

式中：Quk为单桩竖向极限承载力标准值；Qsk为单桩总极限侧阻力；Qpk为单桩极限端阻力标准值；u为桩身周长；qsik为单桩第i层土极限侧阻力标准值；qpk为单桩极限端阻力标准值；Ap为桩端面积；λp为桩端土塞效应系数，对于闭口钢管桩λp=1，对于敞口钢管桩按式(2)、(3)取值；li为单桩第i层土桩身长度；hb—桩端进入持力层深度；d为钢管桩外径；

从上述公式可以发现，没有考虑钢管桩壁厚对其单桩竖向极限承载力的影响。而改变钢管桩壁厚会使桩体端部面积增大使得桩端承载力发生改变。同时减少了钢管桩内土体与钢管桩的接触面积和钢管桩内土体量等，从而对桩体的土塞效应造成影响。而土塞效应的改变也会使钢管桩的单桩竖向极限承载力发生改变。

在工程实践中，钢管桩的竖向承载力计算一直是个难题，而承载力计算其中之一关键点是如何考虑土塞效应。因此在分析钢管桩的单桩竖向极限承载力前，首先要对其土塞效应进行判断。根据土塞效应在钢管桩桩体内的受力特点，一般可分为完全闭塞和不完全闭塞。当钢管桩完全闭塞时，钢管桩此时的状态会像闭口桩一样将周围土体排开因此改变壁厚时其桩底面积也不会改变，钢管桩的竖向承载力也将不会发生改变。而不完全闭塞则是桩体贯入过程中土体继续涌入，土塞高度不断增加，相对于桩有一定的位移。对于大直径钢管桩几乎不向桩周排土,挤土效应非常弱,在桩体贯入的过程中土塞效应完全闭塞的可能性非常小。但由于海洋平台基础建设所用到的钢管桩的直径和贯入度较大，所以即使土的闭塞效应很小，但是大体积的土芯依然会对承载力造成影响。

对于土塞效应的判断，国内外已有许多代表性的土塞效应计算方法，如：小泉法、改进静力平衡法等。其中小泉法比较直观的反应了壁厚对桩体土塞效应的影响，因此下面对小泉法进行介绍。这种方法是在考虑了桩土闭塞效应的基础上将有效面积换成代表桩端封闭面积的办法：

(4)

(5)

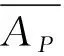
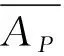
(6)

式(6)中α即为闭塞率

同时通过上式也可以非常直观的发现当钢管桩壁厚增加时其开口桩的闭塞率与桩端有效面积增大。最终使得桩端极限承载力增大。

2 数值模型的选用及建立

2.1.1 桩体模型

运用ANSYS有限元分析软件建立三维实体模型，采用SOLID65实体单元。桩体采用线弹性模型，弹性模量E为210GPa，泊松比为0.25，密度为8010kg/m3。桩体外径为1m，壁厚选取0.05m-0.09m。桩长20m，入土深度15m。

2.1.2 土体模型

土体模型采用圆柱体，径向范围取 10倍桩径[4]，为10m，钢管桩内土体高度为10m。土体单元为SOLID65，弹性模量E为0.25GPa，泊松比为0.4，密度为2000kg/m3，黏聚力为19，摩擦角取为32°，膨胀角为30°。对桩身与土体的作用进行接触分析，接触面上的刚体目标面为TARGE170，接触面为CONTA173单元。设置钢管桩管内的摩擦系数MU为0.2。具体工况如表1所示。网格划分时尽可能保证均匀，如图1所示。

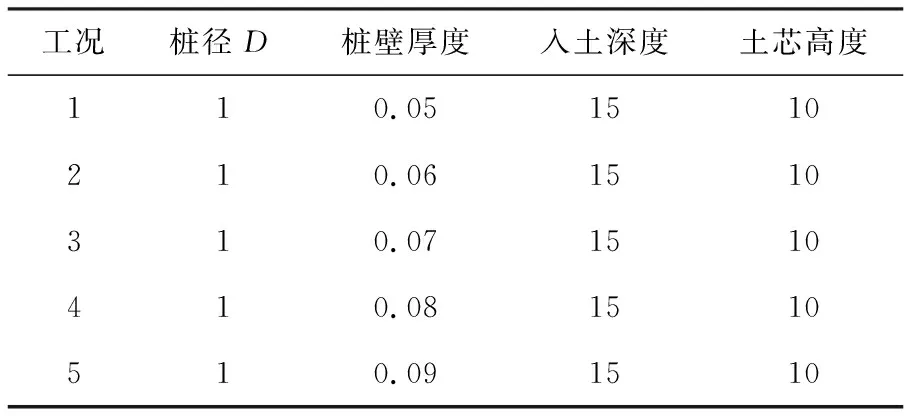
表1 模拟工况 m

2.2 加载方法及分析步骤

将竖向荷载定义为表面荷载均匀地施加在钢管桩桩顶，此时钢管桩在竖向力作用下产生相应的沉降位移。施加竖向荷载为4 MPa，加载方式为逐级加载，共分8级，每级加载0.5MPa。重力加速度g设为9.8m/s2。以模型顶端沉降位移为观察对象绘制Q-S曲线，从而研究荷载位移情况。

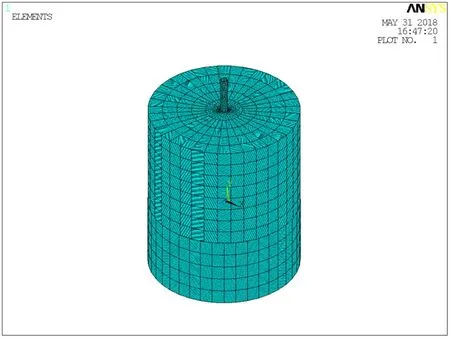
图1 ANSYS有限元模型

2.3 模型分析

通过对5种不同壁厚钢管桩进行逐级加载得到各尺寸各级Y方向桩顶沉降位移云图，限于篇幅每种尺寸位移云图只列出其关键点的位移云图如图2～6所示：

将过程中每级加载的面荷载换算为加载的压力，再根据之前逐级加载得到的各尺寸钢管桩的位移云图绘制荷载—位移曲线如图7所示。可以发现几项Q-S曲线皆为典型的陡降曲线。根据(JGJ106-2014) 建筑基桩检测技术规范可知单桩竖向极限承载力可根据沉降随荷载变化的特征确定：对于陡降型Q-S曲线，应取其发生明显陡降的起始点对应的荷载值。

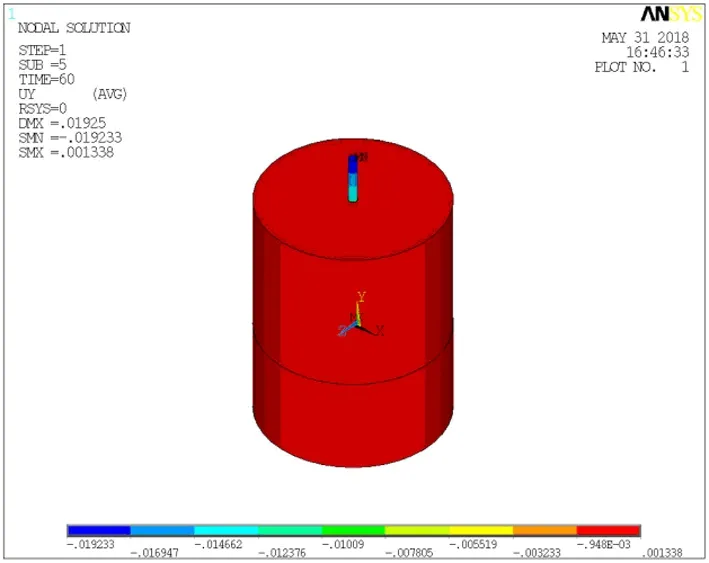
图2 0.05m壁厚钢管桩Y方向位移云图

图3 0.06m壁厚钢管桩Y方向位移云图

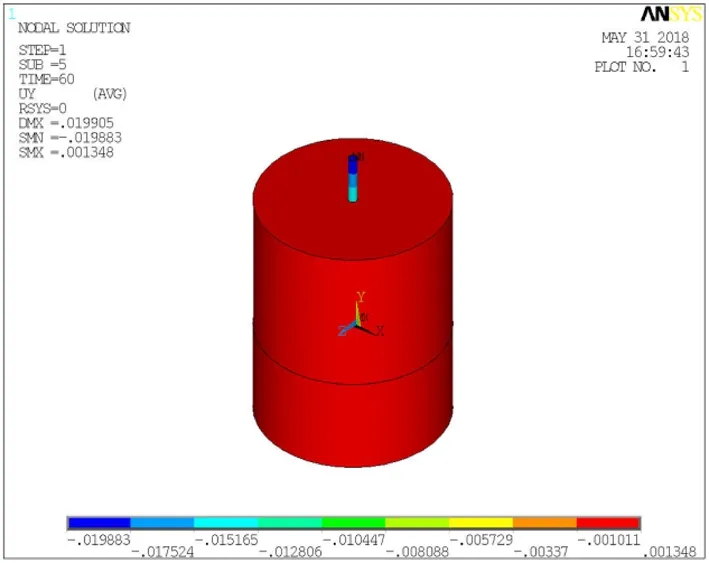
图4 0.07m壁厚钢管桩Y方向位移云图

通过上述各图变化曲线确定其最大竖向荷载并进行计算，得出结果如表2所示：

表2 各尺寸钢管桩竖向承载力

从上表可以看出桩顶承载力随管桩壁厚增加而增大，采用数值分析中的最小二乘法分别使用指数函数、线性函数、对数函数、幂函数和多项式等5种常用函数形式对其变化趋势进行拟合[6]。各函数拟合曲线如图8所示。图中各函数为拟合函数，R2代表其相关系数。

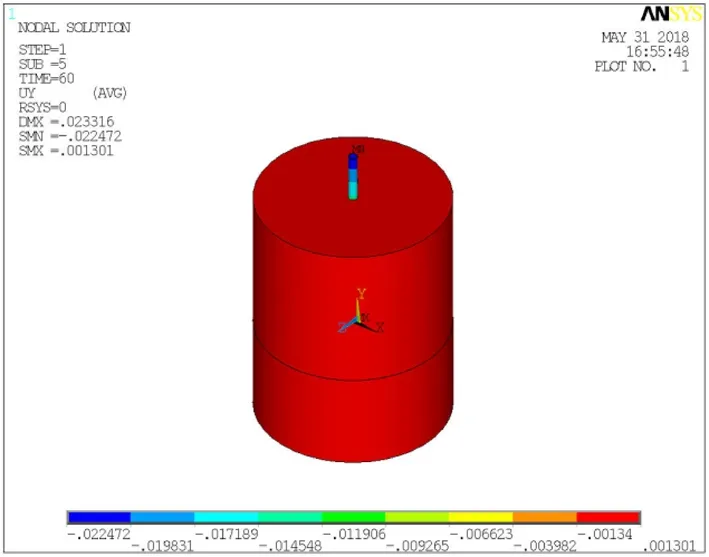
图5 0.08m厚钢管桩Y方向位移云图

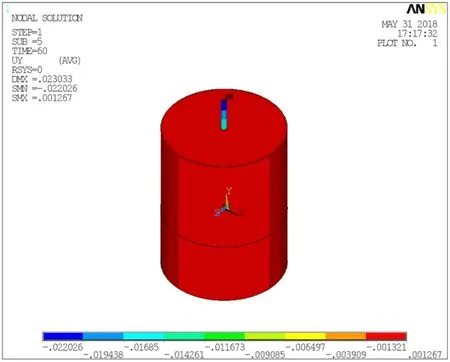
图6 0.09m壁厚钢管桩Y方向位移云图

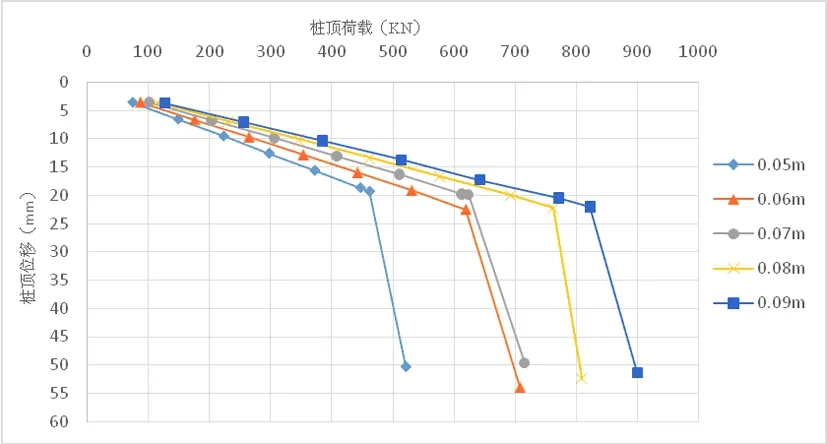
图7 各尺寸壁厚钢管桩Q-S曲线

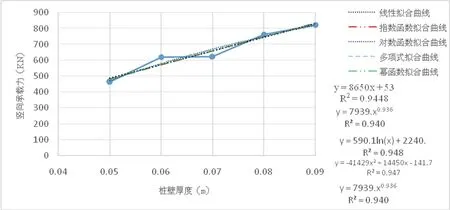
图8 各函数拟合曲线

根据上图可以看出指数函数拟合的相关系数较低只有0.921。剩余四种拟合函数的相关系数都在0.94以上。对数函数拟合的相关系数值最高为0.9486，但线性函数和多项式函数也高达0.9448和0.9478差距很小。通过对拟合函数的使用便捷性和相关性的综合考虑，选择线性函数为桩壁厚度和桩顶的竖向承载力的关系式。

3 结 论

通过理论分析和建立的ANSYS有限元分析模型及其计算结果进行分析论述得出以下结论：

(1)通过小泉法判断钢管桩的土塞效应。钢管桩在不完全闭塞情况下，钢管桩的竖向承载力随着壁厚的增加而增大。但是壁厚增大会使桩体贯入难度增大以及经济成本增加。因此在工程中应当合理选择管桩的尺寸。

(2)通过分析了在地质相同、土塞高度相同和桩端进入持力层深度相同情况下，桩体竖向承载力随桩壁厚改变的变化趋势。对变化趋势采用各种常见函数进行拟合，发现线性函数的相关系数较高且便于研究使用。判断桩体竖向承载力与桩体壁厚为线性函数关系。而《建筑桩基技术规范》(JGJ94-2008)中钢管桩单桩竖向极限承载力计算公式并没有考虑壁厚变化带来的影响。因此当桩体壁厚变化时可根据桩端竖向承载力随壁厚的变化趋势加入比例系数，为今后考虑壁厚变化情况下的大直径钢管桩竖向承载力计算提供参考。