钢管桩静力拔桩侧摩阻力的计算对比分析

， ， ， ， ，

(1.中国一冶集团有限公司湖北分公司，湖北武汉430080；2.中国电力工程顾问集团中南电力设计院有限公司，湖北武汉 430071；3.湖北省路桥集团有限公司，湖北武汉 430000;4.武汉理工大学交通学院，湖北武汉 430063)

0 引 言

多数桥梁及水上工程施工都会采用钢管桩作为临时施工平台或施工栈桥的下部基础，一般会根据实际需要的承载能力选取不同规格的钢管桩以及确定不同的打入深度，通常情况下施工结束后是要将临时施工设施拆除并将地基中的钢管桩拔出以便回收利用，然而对于通过不同方式打入地基中的钢管桩，入土深度、桩径、地基土质、土体固结时间等因素的不同都会导致拔桩的上拔力的不同，所以想要将其成功拔出也不是一件非常容易的事，需要前期对拔桩力进行理论计算分析，并据此来选择拔桩设备型号。

目前国内外对侧摩阻力的计算都是参考一定的规范公式，其中美国按照API-RP2A的方法计算[2]，而国内大多参考公路桥涵地基与基础设计规范[3]或建筑桩基技术规范[4]中提供的半经验公式。因为都是有关土力学的计算，且采用的方法不同，所以二者的计算结果也会有所差异[5]。文中就是通过几种不同的工况来对比分析这两种计算方法的差别，为同类工程提供理论指导。

1 计算方法原理

1.1 国外计算方法

文中涉及的桩土摩擦力计算方法主要是API-RP 2A中的计算方法，由此得到的侧摩阻力计算公式为：

(1)

fv=Ksp0tanφ′

(2)

p0=γz

(3)

其中:Fv为侧摩阻力；r为钢管桩半径；Ks为水平土压力系数，一般取值0.5～1.0，表示水平与垂直有效正应力之比；p0为土层有效覆盖土压力；γ为覆盖土层土重度；φ′为桩与土之间的摩擦角,一般桩土摩擦角与土的内摩擦角之比为0.6～0.7。

该计算方法的原理是认为桩与土的侧摩阻力主要是由于计算截面之上土层对桩的挤压引起的，而桩周土对桩的水平压力又与竖向土压力有关，所以上述计算方法从竖向土压力入手，进而得出桩土侧摩阻力。

1.2 国内计算方法

国内对于拔桩过程侧摩阻力的计算并无相对应的理论公式，一般参照摩擦桩单桩轴向受拉承载力计算方法计算，据此可得桩侧摩阻力计算公式为：

(4)

其中:qik为土层极限侧阻力标准值；u为桩身周长；αi振动沉桩对各土层桩侧摩阻力的影响系数，对于锤击、静压沉桩和钻孔桩，αi=1.0；li为土层厚度。

该计算方法主要以经验值为主进行计算，桩侧摩阻力是根据大量的实验得出的结果，具有较好的可信度，但取值不同对计算结果影响较大。

2 计算结果对比

为了较好的对比分析这两种计算方法的区别，下面将分三类不同的工况分别用这两种方法计算桩侧摩阻力[6～7]。

2.1 不同入土深度计算

通过假定土质情况相同、桩径相同，而计算不同的入土深度对应的桩侧摩阻力，为了能够更好地分析桩长的影响，假定土层是单层土，为可塑黏性土，桩径设为630mm,入土深度取值范围为10～30m,梯度设为2m。

查阅相关资料可得可塑黏性土的参数如下表：

表1 可塑黏性土参数表

现分别用上述两种计算方法对不同的入土深度进行计算，计算结果见图1。

图1 桩侧摩阻力与入土深度的关系

由计算结果及图表对比可以看出在入土深度较小时两种计算方法的计算结果比较接近，随着入土深度的增加，二者的差别也逐渐增大；同时入土深度对第一种计算方法的桩侧摩阻力影响较大。

2.2 不同桩径计算

针对不同桩径，选取入土深度为17m，土层还是为单一的可塑黏性土，桩径取值范围为200～1500mm,梯度为100mm,计算结果见图2。

由上述计算结果可知，随着桩径的增大，两种计算方法的结果差别也是逐渐增大，但是差值增大趋势并不像入土深度那样明显；另外可以看出国外计算方法的摩阻力值随着桩径增大而增大的趋势更大。

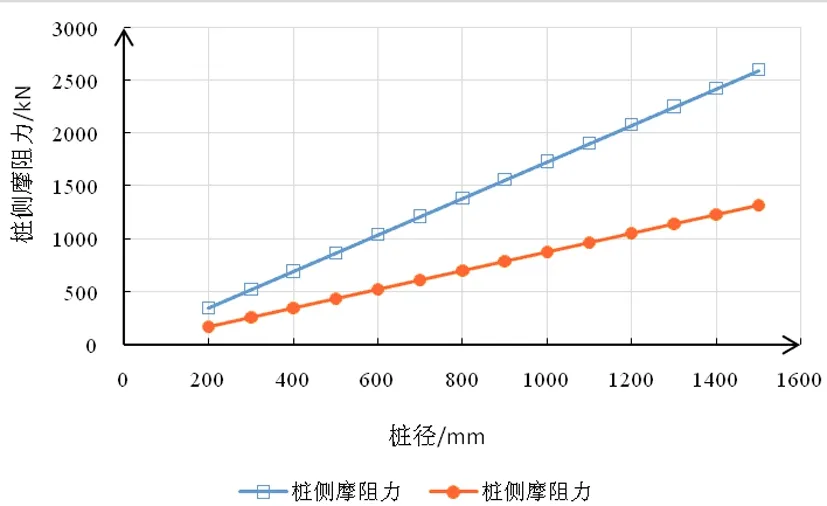
图2 不同桩径的桩侧摩阻力

2.3 不同土质计算

为了较好的分析土质对计算结果的影响，在此对于不同的土质还是取单层土，桩径和入土深度分别取600mm和15m，土质分类如下表：

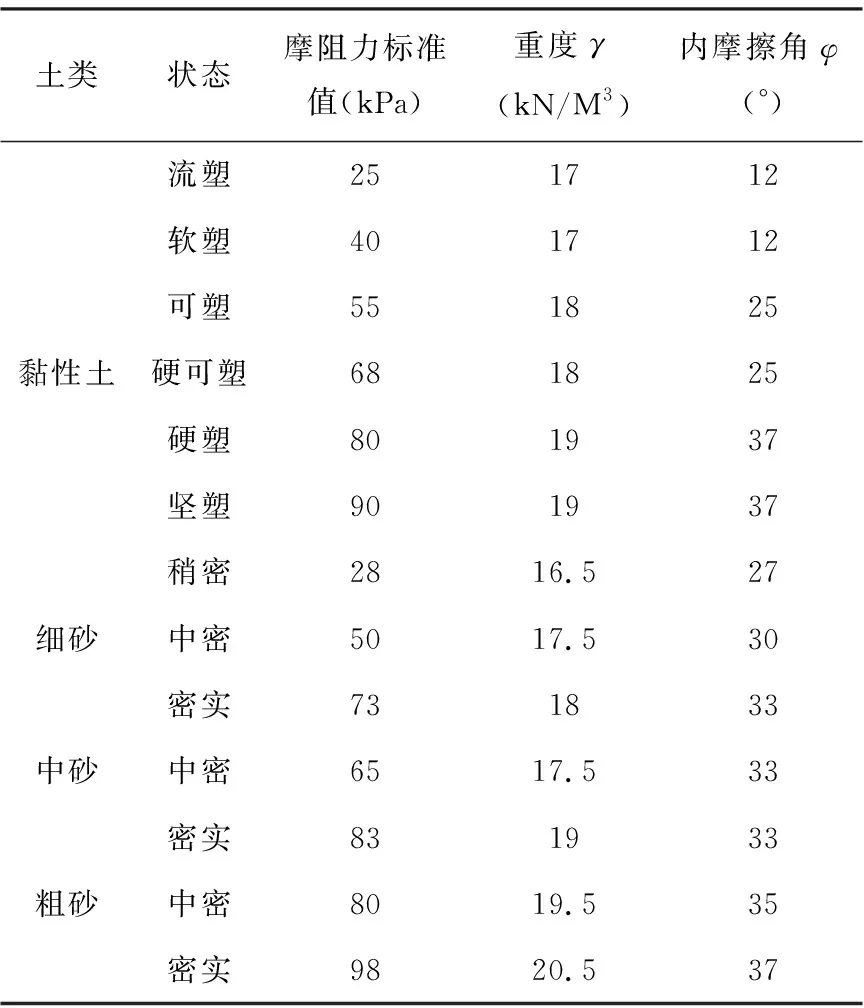
表2 土质分类表

对于上表中不同的土质计算结果见图3。

图3 不同土质桩侧摩阻力

由上述计算结果可以看出和前两种工况一样，国外计算方法的摩阻力都比国内计算方法的摩阻力大；同一类土，随着含水率的降低和颗粒的增大摩阻力也随之增大。

3 计算结果分析

3.1 不同入土深度计算结果分析

对于上述不同入土深度桩侧摩阻力的计算结果，两种计算方法的差值之所以是三种情况中最大是因为国外计算方法是由竖向土压力推导水平土压力，进而沿深度方向积分得到桩侧摩阻力，而桩侧摩阻力是如图深度的二次函数；而国内计算方法的桩侧摩阻力只是深度的一次函数，而且还和侧摩阻力标准值有关，而这一数值只能根据由大量实验数据总结的取值范围取值，这对计算结果的影响较大。

3.2 不同桩径计算结果分析

对于不同桩径桩侧摩阻力，由计算结果分析可得：国外计算方法对于水平土压力的处理是根据实际情况推导的，即土压力随入土深度线性增大[6]，而国内计算方法是根据实验数据取了一个中间值作为单位长度方向土压力的代表值，这两种处理的方式是引起两者计算结果差别的主要原因，而桩径的不同也会增大二者的差别。所以对于单层土积分法会比较接近实际情况，因为如果单一土层深度较深，取中间值的误差会比较大，对计算结果影响也会较大，就会造成理论计算和实际差距较大；而对于多层土两者差别就会减少。

3.3 不同土质计算结果分析

对于不同土质的情况，由计算结果分析可得:黏性土是比较特殊的，它对桩侧摩阻力的影响并不像其他的土一样，由图3可以看到，对于细砂、中砂、粗砂，两种计算方法的结果虽不相同，但是变化趋势是一样的，而对于黏性土二者的变化却并不一样，主要是因为含水率对侧摩阻力影响较大，而对土的重度和内摩擦角影响较小，所以对于黏性土两种计算方法的差别会比较大，但是实际上含水率的不同对桩侧摩阻力的影响应该是较大的。

4 结 论

通过分不同的入土深度、不同的桩径、不同的土质这三种工况对API-RP2A计算方法和国内规范法计算对比分析可得出以下结论：

(1)国外计算方法通过理论推导的方式计算得出桩侧摩阻力，虽然是从最基本的计算推导误差较小，但是其中和的取值也会造成一定的差别；而国内计算方法是根据经验数据计算，取值有较大的浮动，主要以经验为主。二者的计算结果虽然有差别，但是通过分不同工况计算可以看出对于入土深度较小以及桩径也较小的情况二者计算的结果还是比较接近的，由此可见对于小桩径、小桩长的情况，两种理论计算的结果应该和实际比较接近。

(2)两种计算方法各有可取之处，也各有存在不足的地方，相比较而言，积分法采用的理论推导会比较接近实际情况，总体会略好一些。

(3)文中是为了比较入土深度、桩径、土质等因素对两种计算方法的影响，所以假设的情况可能会与实际情况略有不同，所以在今后的研究中应该假设多层土的情况分析。