面向避障和紧凑的浮动滚子推杆盘形凸轮机构尺寸综合问题

林梦杰 李延平 常 勇

集美大学机械与能源工程学院，厦门，361021

1 问题的提出

2010年，源于引进德国海德堡高速印刷机机构后消化吸收的工程实际背景，笔者归纳出以下具有一般性的浮动滚子推杆盘形凸轮机构问题［1］：

（1）Ⅰ类尺寸综合问题。已知从动构件系统运动学尺寸、输出件推程起始终止位置和角位移规律，以及许用压力角、滚子中心在连杆上具体位置等条件，求解凸轮轴心容许选择区域、凸轮基圆半径许用取值范围等。

（2）Ⅱ类尺寸综合问题。已知从动构件系统运动学尺寸、输出件推程起始终止位置和角位移规律，以及许用压力角、凸轮轴心位置和滚子中心位居连杆某一方位线等条件，求解滚子中心容许选择区段、凸轮基圆半径许用取值范围等。

笔者通过建立坐标系、划分推程区段和引入“浮动数轴”、“瞬时/整程区间套”等新概念，圆满解决了浮动滚子推杆盘形凸轮机构的狭义Ⅱ类尺寸综合问题。

德国海德堡高速印刷机中的浮动滚子推杆盘形凸轮机构见图1，该机构由凸轮1、连杆2、摇块3、滚子4（铰接于连杆上）、摇杆5和机架0组成。原动件（凸轮1）通过滚子4和连杆2，驱动输出件（摇杆5）在推程起始、终止位置（O20A、O2mA）间实现预期运动输出。

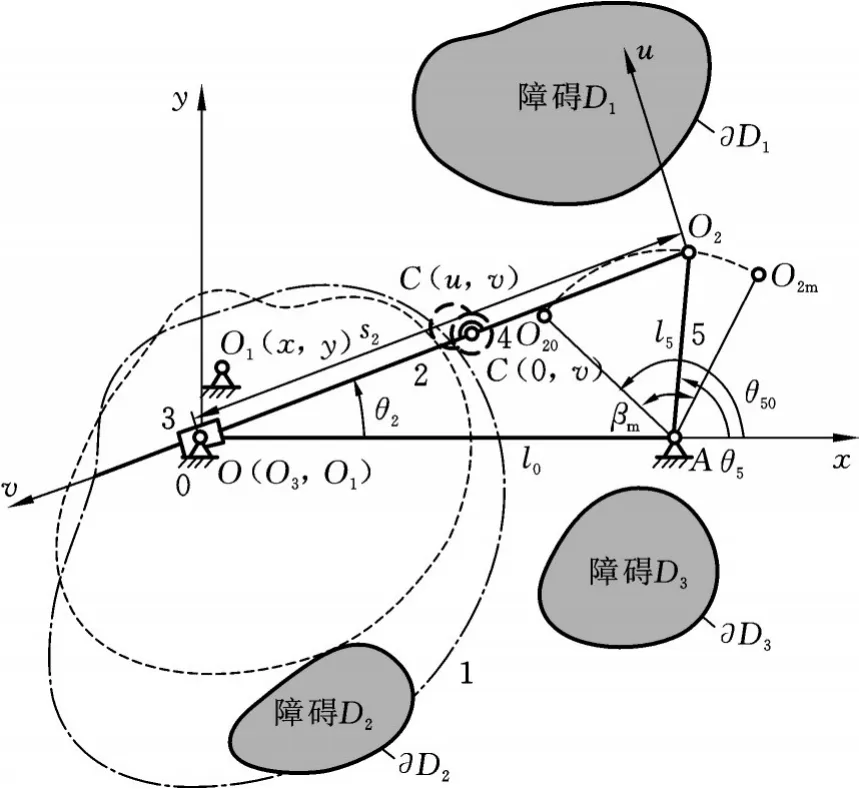
图1 浮动滚子推杆盘形凸轮机构的原始形态及演化形态Fig.1 Original/evolutionary form of a disk cam mechanism with a floating roller

2012年，随着对海德堡高速印刷机机构消化吸收的深入，通过“释放”滚子中心，即在连杆平面上任意选取滚子中心位置，笔者提出了更具一般性的浮动滚子推杆盘形凸轮机构问题［2］。通过引入“浮动坐标系”、“瞬时/整程区域套”和“最经济搜索带域”等概念，圆满解决了浮动滚子推杆盘形凸轮机构的广义Ⅱ类尺寸综合问题，即:已知从动构件系统运动学尺寸、输出件推程起始终止位置和角位移规律，以及许用压力角、滚子中心位居连杆平面和凸轮轴心位置等条件，求解滚子中心容许选择区域、凸轮基圆半径许用取值范围等。

德国海德堡高速印刷机中的浮动滚子推杆盘形凸轮机构具有以下显著结构特征：①凸轮1、摇块3与机架0构成复合铰链O1（O3），即凸轮和摇块轴心O1、O3重合；②滚子中心C位于连杆方位线O2O3上。

2010年笔者严格恪守“显著结构特征”①和②，相应提出的尺寸综合方法属于纯粹性“消化吸收”［1］。2012年笔者更改了“显著结构特征”②，释放滚子中心C于连杆平面Σ2上，属于实质性“改进创新”［2］。

由于部件、元器件和线路的调整变更和重新布置等，机构“周边环境”发生了复杂显著变化，机构与环境发生“肢体冲突”的概率陡然增加。

若采用笔者2012年提出的广义Ⅱ类综合方法［2］，无论凸轮顺时针还是逆时针转动，皆无法避免凸轮和（或）滚子与部件、元器件及线路发生碰撞干涉，解得的尺寸不成立，广义Ⅱ类综合方法“失效”。采用笔者2010年提出的狭义Ⅱ类综合方法［1］则更有过之。

上述尝试求解表明：采用广义、狭义Ⅱ类尺寸综合方法［1⁃2］难以适应变化了的“周边环境”，无法取得成功避障的机构尺寸解。部件、元器件和线路的调整变更和重新规划布置等，占据了“解机构”的运动空间，对机构运动着实构成了“障碍”。

“避障和紧凑”已有诸多研究成果［1⁃9］，基于“双释放（释放滚子中心和凸轮轴心）的基本思想（见图1中演化构型（虚线）的凸轮轴心O1（x，y）、滚子中心C（u，v）），根据Ⅰ类尺寸综合方法［3］，笔者分析推理得到最优凸轮轴心O**1是“整程避障成功”的最适任解，给出障碍集{Di}、许用边界{∂Di}基础性的概念，提出滚子、凸轮“整程避障成功”解析判据以及“简约搜索区域求解凸轮轴心O1、滚子中心C解区域的遍历搜索方法，提出“机构紧凑尺寸解”求解方法，以解决面向避障和紧凑的浮动滚子推杆盘形凸轮机构尺寸综合问题。

需要指出的是：部件、元器件和线路的调整变更和重新布置等，已保证不占据从动构件系统运动空间——不构成障碍。本文的核心和关键是探索解决“凸轮和滚子”的成功避障问题。

2 面向避障和紧凑的浮动滚子推杆盘形凸轮机构尺寸综合问题的准确描述

面向避障的机构尺寸综合问题的准确描述如下。已知：①障碍集。障碍集D1～Dn的形态特征，相对从动件系统的位置分布；②从动件系统。机架长度 l0，摇杆长度 l5，摇杆初位角 θ50、行程角 βm，推程、回程运动角Ф0和Ф’0，推程、回程运动规律，滚子半经rr，推程许用压力角［α1］，凸轮转动方向。求解：“整程避障成功”凸轮轴心O1、滚子中心C的解区域；机构紧凑尺寸解。

3 理论基础和重要推证结论

3.1“固定坐标系Oxy”和“浮动坐标系O2uv”的概念

基于海德堡高速印刷机机构的浮动滚子推杆盘形凸轮机构的原始构型、演化构型见图1。两种构型的凸轮和滚子分别用点画线、虚线描述表达。

固定坐标系Oxy指固连于机架平面Σ0上，以O为原点、O→x为x轴正向、O→y为y轴正向的直角坐标系。浮动坐标系O2uv指固连于连杆平面Σ2上，以O2为原点、O2→u为u轴正向、O2→v为v轴正向的直角坐标系。

3.2 滚子中心由C（uC，vC）→（xC，yC）的坐标变换

滚子位于连杆平面Σ2上，（uC,vC）为滚子中心C的浮动坐标系坐标。本文研究避障问题，需求解滚子中心C的固定坐标系坐标（xC,yC）。可据坐标变换公式

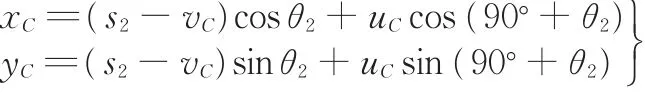
解得xC和yC。上式是后文的求解计算基础。据上式，有

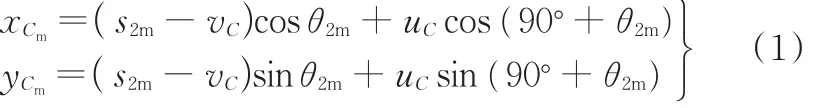
式中，s2m、θ2m分别为推程终止位置的连杆长度、连杆位置角。

3.3 机构Ⅰ类尺寸综合问题的重要结论［4］

3.3.1 整程区域套Γ*(x,y)和整程边界Γ*(x,y)

若在连杆平面Σ2上给定某一滚子中心C，即对应存在凸轮轴心O1的解域——整程区域套Γ*（x，y），则对应边界为整程边界∂Γ*（x，y），见图 2［3］。

3.3.2 最优凸轮轴心O**1及其性质［3］

整程区域套 Γ*（x，y）呈半封闭、类角形的形态特征［3］。给定滚子中心C，存在最优凸轮轴心角点O**1，即取得凸轮最小基圆半径r0min，见图2。

3.4 凸轮工作轮廓最大向径rmax

据图2推知

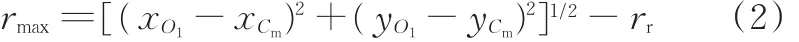
式中，rr为滚子半径；xO1、yO1分别为凸轮轴心O1的x、y坐标（据Ⅰ类尺寸综合方法解得），xCm、yCm

为推程终止位置滚子中心Cm的x、y坐标（据式（1）解得）。

3.5 最优凸轮轴心O**1内涵重要拓展引申

3.5.1 凸轮整周转动的最小占据区域

对应Σ2上同一滚子中心C，凸轮轴心分别取四点，绘出凸轮整周转动占据的4个圆形区域，见图2。显见，凸轮轴心取点的占据区域最小。前述为圆心、小半径划弧，与∂Γ*(x,y)截得的交点和中点。

3.5.2 “整程避障成功”的凸轮轴心最适任解

整程区域套 Γ*（x，y）除外的边界点和内点，皆因在避障和尺寸方面居于劣势，故不予考虑。

4 “整程避障成功”的滚子和凸轮的解析判据

4.1 障碍集{Di}的静占区域、滚子和凸轮的动占区域

4.1.1 障碍集{Di}的静占区域

Σ0上的障碍集{Di}及其许用边界{∂Di}（i=1，2，…，n）见图3。

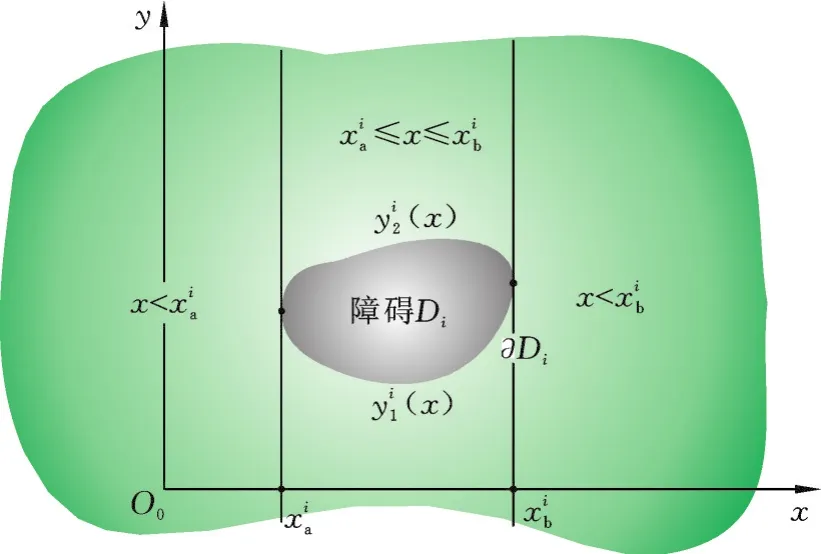
图3 障碍集{Di}及其许用边界{∂Di}Fig.3 Obstacle set{Di}and its allowable boundary{∂Di}

任一障碍Di的静占区域为

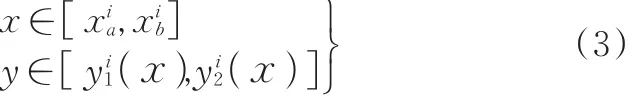
应指出，许用边界∂Di是障碍Di真实边界的外等距曲线，而此“等距”一般取5～8 mm。为使图简约清晰，真实边界未画。后文中各图皆为许用边界{∂Di}。

4.1.2 滚子和凸轮的瞬时/整程动占区域Droll/{Droll}和Dcam/{Dcam}

滚子瞬时动占区域Droll指任一瞬时以滚子中心C为圆心、滚子半径rr为半径的圆形区域。

滚子整程动占区域{Droll}指所有瞬时以滚子中心C为圆心、滚子半径rr为半径的圆形区域的并集。

凸轮瞬时动占区域Dcam指任一瞬时以凸轮工作轮廓为整体边界的盘形区域。

凸轮整程动占区域{Dcam}指以凸轮轴心O1为圆心、凸轮工作轮廓最大向径rmax（图2）为半径的圆形区域。

不难理解，{Droll}和{Dcam}是由无数个瞬时Droll和Dcam构成的无限序列。

4.2 滚子瞬时/整程避障成功的位置特征与解析判据

4.2.1 滚子瞬时/整程避障成功的位置特征

瞬时避障成功的位置特征就是Droll与{Di}相离，即

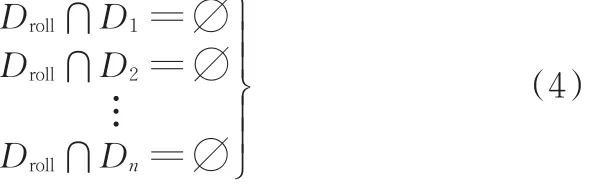
整程避障成功的位置特征就是{Droll}与{Di}相离，即

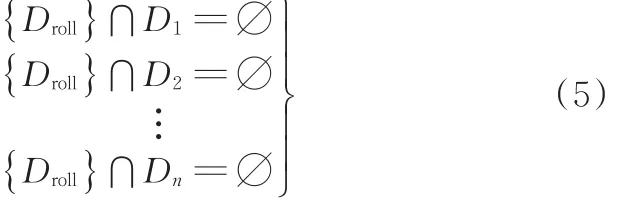
4.2.2 滚子瞬时/整程避障成功的解析判据

瞬时避障成功的解析判据如下：

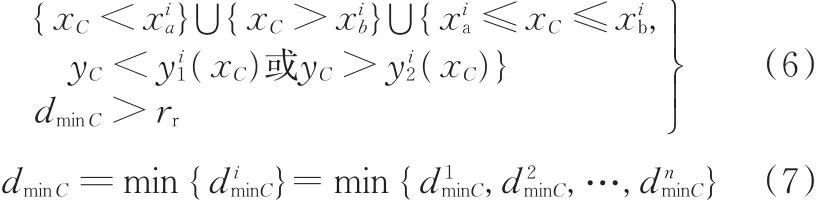
式中，xC、yC、dminC分别为任一瞬时 C 的 x、y坐标和至{∂Di}最小距离；diminC为任一瞬时 C 至∂Di的最小距离。

整程避障成功的解析判据如下：

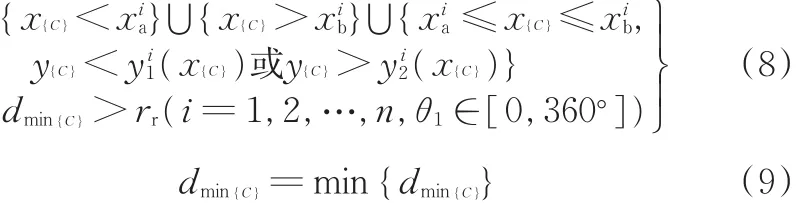
式中，x{C}、y{C}、dmin{C}分别为整程所有瞬时C的x、y坐标和至{∂Di}最小距离。

x{C}=x{C}(θ1)和 y{C}=y{C}(θ1)是 θ1的一元函数。据式（8）对θ1进行等距-离散化，例如取°，参见后文示例。

式（8）包括两层含义：①满足所有障碍{Di}；②满足所有瞬时θ1∈［0，360°］。

因为障碍集{Di}的非时变性以及推程、回程滚子中心C的轨迹重合，据式（8）推知，满足推程 θ1∈［0，Φ0］即满足整程 θ1∈［0，360°］，Φ0为推程运动角。

4.3 凸轮整程避障成功的位置特征与解析判据

4.3.1 凸轮瞬时/整程避障成功的位置特征

瞬时避障成功的位置特征就是Dcam与{Di}相离，即

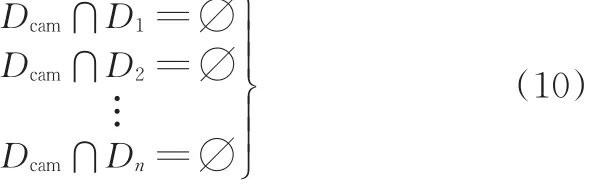
整程避障成功的位置特征就是{Dcam}与{Di}相离，即

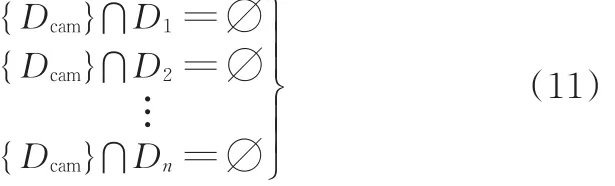
4.3.2 凸轮整程避障成功的解析判据

凸轮整程避障成功的解析判据如下：

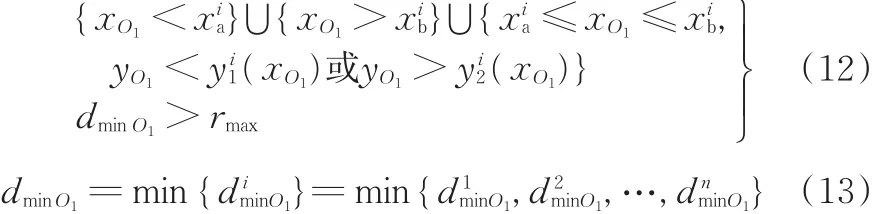
式中，xO1、yO1、dminO1分别为O1的 x、y坐标和至{∂Di}的最小距离。

后文中“避障成功”皆指整程避障成功。

5 避障成功滚子中心C、凸轮轴心O1解区域的遍历搜索求解

遍历搜索求解的策略、路线和方法步骤如下。

（1）选定简约搜索区域Σ[2]。如图4所示，选定简约搜索区域

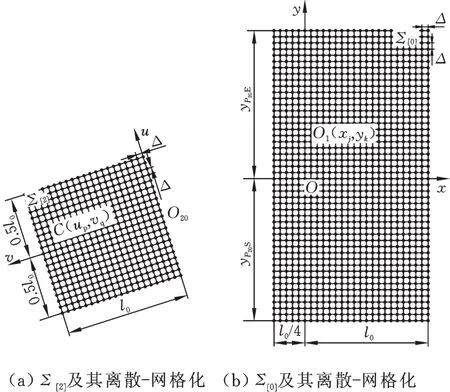
图4 简约搜索区域Σ[2]和Σ[0]的离散-网格化Fig.4 Simplified search areaΣ[2]andΣ[0]

（2）Σ[2]的离散-网格化。对Σ[2]沿u、v方向离散-网格化（图4）：

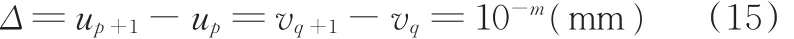
任一网格节点C（up，vq），有

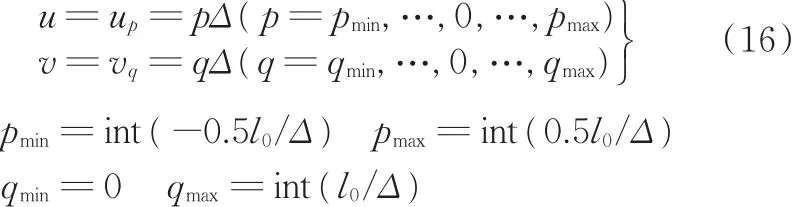
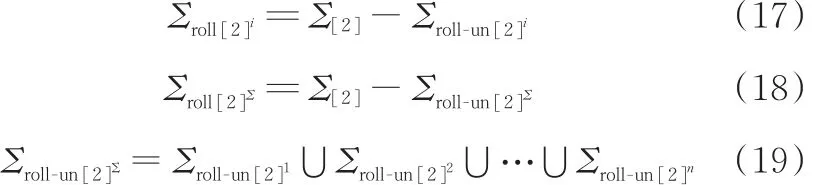
（4）选定简约搜索区域Σ[0]。选定简约搜索区域Σ[0]（图4）：

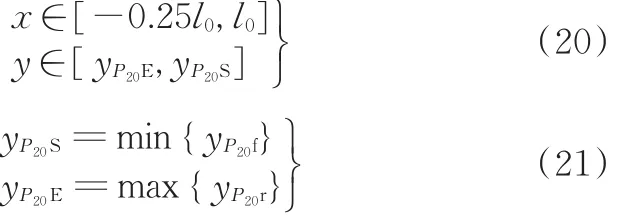
式中，yP20f、yP20r分别为往程前半、后半区段绝对瞬心P20的y坐标。

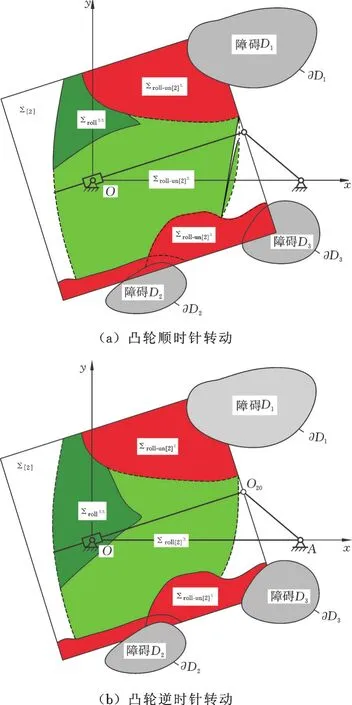
图5 滚子中心C的过程、结果解区域和Fig.5 The process and result solution region of the roll center C and

（5）Σ[0]的离散-网格化。如图4所示，对Σ[0]沿x、y方向离散-网格化：

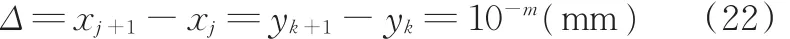
任一网格节点O1（xj，yk），有

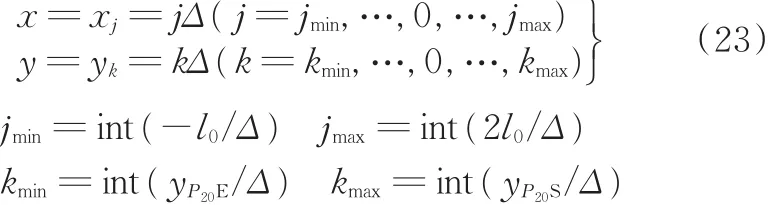
式（15）和式（22）的Δ等同，取决于指数m，据精度要求而定。

（6）滚子避障成功、凸轮轴心位于Σ[0]内的过程解区域 Σcam[0]Σ。对图5的过程解区域 Σroll[2]Σ，遍历取滚子中心C的节点（up，vq）为滚子中心C，根据Ⅰ类尺寸综合方法［3⁃4］解得对应凸轮轴心“角点”，该角点位于Σ[0]内，标浅色。

遍历取 Σroll[2]Σ上各滚子中心节点，图6中生成得到浅色过程解区域，记为Σcam[0]Σ。

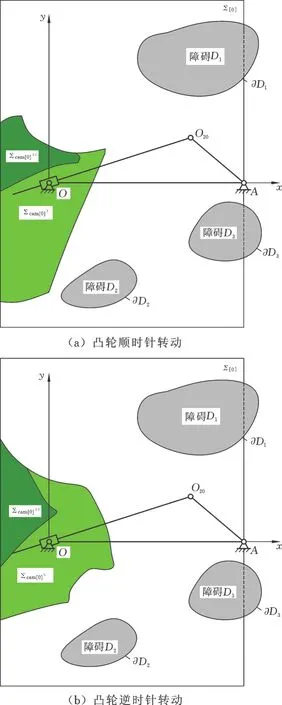
图6 凸轮轴心O1的过程、结果解区域Σcam[0]Σ和 Σcam[0]ΣΣ Fig.6 The process and result solution region of the cam axis O1 Σcam[0]Σ and Σcam[0]ΣΣ

（7）滚子避障成功、凸轮轴心位于Σ[0]内的过程解区反转过来，将与图对应的图5节点(up,vq)标记浅色，生成得到浅色过程解区域，记为Σroll[2]Σ。

（8）滚子和凸轮避障成功凸轮轴心O1的结果解区域 Σcam[0]ΣΣ。对图6浅色过程解区域 Σcam[0]Σ，遍历取凸轮轴心O1的节点(xj,yk)，即凸轮轴心O1，检验校核是否满足式（12）。若满足式（12），标深色；反之，仍标浅色。

遍历取 Σcam[0]Σ，得到深色结果解区域，记为

（9）滚子和凸轮避障成功滚子中心C的结果解区域 Σroll[2]ΣΣ。反过来，将与图6对应的图5节点(up,vq)标深色，得到深色结果解区域，记为

图5～图7的绘制生成，皆基于后文示例已知条件数据。

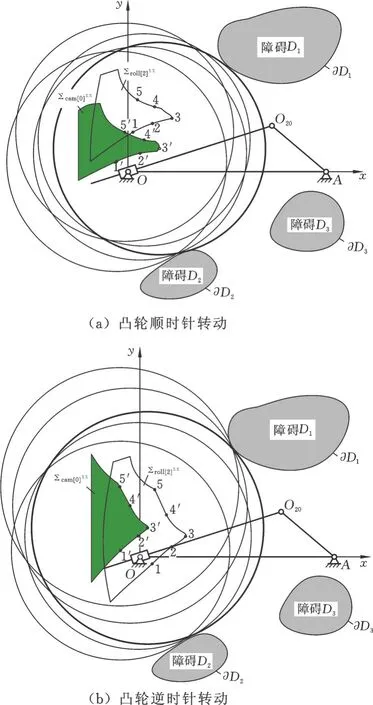
图7 机构紧凑尺寸解（C、O1）的求解Fig.7 Solution of compact size solution（C、O1）

6 机构紧凑尺寸解（滚子中心C、凸轮轴心O1）的求解

根据“最优解常出现在边界”的知识经验（图7），确定最优解步骤如下。

（1）沿解区域Σroll[2]ΣΣ的下侧（靠近连杆侧）、右侧边界和沿逆时针方向，顺次选取滚子中心C的离散点1～5；

（2）对应得到分布于解区域Σcam[0]ΣΣ的下侧（靠近连杆侧）、右侧边界上，也是沿逆时针方向的5个离散点1′、2′、3′、4′、5′，即凸轮轴心O1；

（3）据滚子中心C、凸轮轴心O1的5种组合（1，1′）～（5，5′），据式（2）计算绘出对应的凸轮整程动占区域{Dcam}，即图7a、7b中的5个圆。

分析图7，得到以下重要结论：

（1）无论凸轮顺时针还是逆时针转动，滚子中心C 位于解区域 Σroll[2]ΣΣ的角点3时，凸轮轴心O1也位于解区域 Σcam[0]ΣΣ的角点3′；

（2）凸轮轴心O1取在角点3′，凸轮整程动占区域{Dcam}最小，见图7a、7b中的粗实线圆。

由图7不难看出：凸轮轴心O1取在角点3′，粗实线{Dcam}最充分嵌入、利用了从动件系统和障碍集已占据空间，对环境空间的额外索取达到最小，即最紧凑。

7 机构综合示例

图1中，机架长度l0=140 mm，摇杆长度l5=50 mm，摇杆初位角θ50=140°，行程角 βm=80°，推程选用摆线运动规律，推程运动角Ф0=150°，滚子半经rr=6 mm，许用压力角［α1］=40°，3个障碍静占区域 D1～D3（许用边界∂D1～∂D3数据描述从略），求解：①滚子和凸轮整程避障成功的结果解；②机构紧凑尺寸解。

求解过程如下。

（2）机构紧凑尺寸解。①凸轮顺时针转动。据第6节和Ⅰ类尺寸综合方法［3］，机构紧凑尺寸解为：滚子中心 C（65.20，25.83），凸轮轴心 O1（22.49，16.02），见图 7a。据式（1）解 得 xCm=95.31 mm，yCm=29.14 mm，据式（2）解得 rmax=75.16 mm。②凸轮逆时针转动。步骤同上，机构紧凑尺寸解为：滚子中心C（70.67，4.07），凸轮轴心O1（6.39，19.59），见图7b。据式（1）解得 xCm=95.31 mm，yCm=29.14 mm，据式（2）解得 rmax=83.74 mm。

对比求解上面的计算结果后可知，较之凸轮逆时针转动，凸轮顺时针转动的尺寸更紧凑、更具优越性。