外层腐蚀对输电线路架空地线承载力的影响

邓静伟， 张 宇， 陈 波， 吴永祥

(1. 国网江西省电力有限公司电力科学研究院， 江西 南昌 330096; 2. 武汉理工大学 道路桥梁与结构工程湖北省重点实验室, 湖北 武汉 430070)

输电线路是重要的电力基础设施，关系国计民生，是重要的生命线工程。由于我国国民经济和社会建设的迅速发展，修建了大量的各类输电线路。输电线路长期在野外服役，需要经过不同地形和气候复杂地区，因此容易在恶劣环境作用下发生输电线的腐蚀。输电导线通常采用钢芯铝绞线构造，外层铝股不容易发生腐蚀。而地线多为镀锌钢绞线，因此地线外层钢股容易发生腐蚀损伤，并进一步引起地线的破坏，这将造成严重的经济损失和次生灾害[1～3]。随着西电东送与超特高压输电工程的建设，越来越多的各类输电线路将被建造于地形和环境复杂地区。因此，结合我国输电线路工程灾变的实际，开展输电地线腐蚀性能的研究具有重要的科学意义和工程价值[4～6]。

目前输电线路设计无法考虑输电地线不同股线的力学性能，不能考虑股线腐蚀程度对其承载力特性的影响。随着对输电线路设计建造和维护要求的不断提高，要求对输电地线在腐蚀作用下的承载力特性有更多的了解和掌握。因此，国内外越来越重视输电地线腐蚀性能评估工作。但目前针对输电地线腐蚀效应的研究工作非常有限，特别是没有考虑腐蚀程度对输电地线承载力的影响[7,8]。基于此，本文研究了自重荷载作用下腐蚀输电地线的承载力特性问题。首先基于非线性有限元理论建立了输电地线的分析模型，随后建立了腐蚀输电地线的非线性承载力分析方法，建立了腐蚀地线非线性迭代收敛准则。以我国南方某实际输电线路的地线为背景，研究了自重作用下腐蚀输电地线的承载力特性并考察了不同参数对其承载力的影响。本文研究表明：地线参数和腐蚀程度对其承载力具有较为显著的影响。

1 输电地线模型

输电地线通常采用多根镀锌钢丝逐层绞制而成，如图1所示。多层钢股线按照一定的螺旋升角紧密缠绕在内层钢芯外侧。同一层股线具有相同的直径。对于地线而言，随着螺旋升角的减小，单位轴向长度内外层股线缠绕的匝数越多、股线缠绕越密集。

图1 输电地线构造示意

架空地线是一种典型的空间柔性结构，因此其静动力响应具有明显的非线性特性，只能承受拉力不能承受压力。依据非线性有限元分析理论，可采用三节点索单元模拟输电地线的承载力特性。地线单元上任意一点的位移(u,v,w)可表示为：

(1)

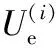
(2)

地线单元的应变ε可依据格林应变得到：

(3)

(4)

式中：ξ为地线上任意点到局部坐标原点的弧长；L为单元长度。通过建立不平衡张力和位移增量的关系可求得地线单元的刚度矩阵K：

K=KE+KD+KS

(5)

式中：KE为弹性刚度矩阵；KD为初始位移刚度矩阵；KS为初始应力刚度矩阵。

(6)

(7)

(8)

式中：E为架空地线弹性模量；A为腐蚀地线的横截面积；σ为轴向应力向量；BL，BN为线性和非线性应变矩阵。

2 输电地线非线性分析方法

确定了地线的单元刚度矩阵后即可组集形成整体坐标系下的地线总刚度矩阵，可采用非线性迭代算法确定地线结构在荷载作用下的张力。整体坐标系下可将所有单元的刚度矩阵和荷载向量进行组集形成整体刚度矩阵K和整体荷载向量P。自重作用下地线的受力方程可表示为[9,10]：

Kx=G

(9)

式中：x为腐蚀输电地线位移响应；G为腐蚀地线自重荷载。

本文采用Newton-Raphson法和增量法相结合的方式对输电地线的平衡方程进行求解，采用位移收敛准则。假定结构初始位移为x(0)=0，根据求解所得新平衡形态下的地线位移，可以重新形成结构的不平衡力向量Δψ1。重复以上步骤直至所得位移差范数满足设定的收敛容差，则迭代过程结束：

‖x(n+1)-x(n)‖2≤Tol

(10)

式中：x(n)和x(n+1)分别为第n，n+1次迭代的结果；Tol为预先设定的大于零的收敛容差。

本文以我国南方山区某输电线路为实际工程背景进行了腐蚀地线承载力特行分析研究。地线型号GJ-80，档距300 m。地线为三层共计19根股线结构，从内到外依次第一层为1根股线，第二层为6根股线，第三层为12根股线。单根股线直径为2.3 mm，地线总直径为11.5 mm。地线横截面积为78.94 mm2，弹性模量为185 GPa，单位长度重量为628.4 kg/m，绞线破断拉力为90.23 kN，拉断应力为1143 MPa。根据GB 50545-2010《110～750 kV架空输电线路设计规范》，架空地线在弧垂最低点的设计安全系数不应小于2.5，地线平均运行张力上限为额定破断拉力的25%。地线各股标识如图2所示。由于长期在野外恶劣自然环境下服役，因此地线外层不可避免地发生了腐蚀，导致外层截面损失。本文对大量现场取样腐蚀架空地线扫描电镜截面进行了观察分析，结果表明其腐蚀区域接近于新月形。图3给出了输电地线外层股线腐蚀区域示意图。

图2 输电地线各股标识

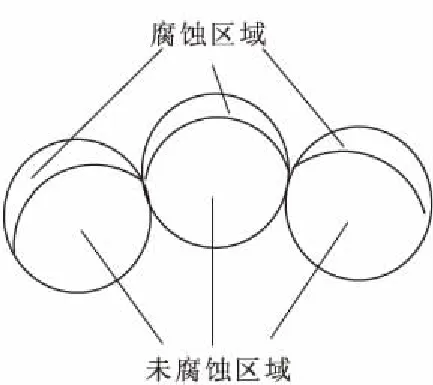
图3 输电地线腐蚀示意

3 输电地线承载力分析

基于前述建立的基于非线性有限元的承载力分析方法，本文在此研究了腐蚀输电地线在自重作用下的承载力特性。分析过程所采用的地线腐蚀状况依据实测结果确定，其股线腐蚀面积占整个股线横截面积的20%。图4 显示了不同垂跨比下腐蚀地线各股线的应力结果。由图中结果可知，弧垂对腐蚀地线的应力影响很大。地线弧垂为0.5%时，各层股线的应力均达到约620 MPa。但随着弧垂逐渐增大，各股应力迅速减小。地线弧垂为1.0%时，各层股线的应力迅速减小到约300 MPa，减小幅度超过一半。再进一步增大弧垂，则各股线应力开始缓慢减小，地线弧垂为2.0%时，各层股线的应力已经下降到约140 MPa。再进一步增大弧垂对股线应力的影响已经较小。同时从分析结果还可以发现，同一层的不同股线，其受力几乎完全一样。

图4 不同垂跨比下股线应力

图5给出了20%腐蚀下不同层股线的轴向应力对比。结果表明：从里至外不同层的轴向应力发生小幅减小，但总体而言不同层股线的应力非常接近，并且这种变化趋势随着地线弧垂的增加也不会发生改变。

图5 不同垂跨比下股线应力

4 参数研究

上述分析结论是在地线档距为300 m，腐蚀面积为20%的情况下得到的。实际输电地线档距差别较大，并且不同地区的地线腐蚀程度也存在一定程度的差异。因此本文在此针对地线参数进行了相应的参数研究。选取了200，300，400，500，600 m等5种典型的地线档距参数，考察了地线轴向应力的变化特点，其结果如图6所示。由图6结果可知：地线档距对轴应力有一定程度的影响，随着档距的增加，内层钢芯的轴应力迅速增加。档距200 m时内层钢芯轴应力约为100 MPa，当档距增加为600 m后，应力可达300 MPa，应力增幅呈线性关系，增幅达300%。第二层和第三层股线应力的变化规律与内层钢芯一致，并且同一层内各根股线的应力相同。图7给出了2%弧垂和不同档距下各层股线应力的对比结果。由图中结果可知，从内至外股线应力逐渐增加，内层钢芯的应力略大于外层股线的应力，并且这种差异随着地线档距的增大而逐渐增加。

图6 档距对地线垂跨比的影响

图7 档距对地线垂跨比的影响

本文还研究了外层股线腐蚀面积对地线承载力的影响。选取了5%，10%，15%，20%等4种腐蚀比例参数。图8给出了外层腐蚀面积对股线应力的影响。由图中结果可知：随着外层股线腐蚀面积的增加，地线有效承载面积逐渐减小，但同时地线的自重也逐渐减小。因此其股线应力基本保持不变。对于外层股线而言，各层中的不同股线的应力相同。

图8 腐蚀面积对股线应力的影响

通过对比不同腐蚀面积下不同层股线应力的结果，可以发现与档距和弧垂的参数研究结果类似的结论。地线各层股线应力由内至外逐渐增加。此外，由图8还可发现不同腐蚀程度下，地线各层之间的应力差基本保持不变，这表明外层地线腐蚀对地线各层中的应力分布影响较小，各层股线应力基本等同变化。这一点与图5，7所显示的弧垂参数和档距参数的影响明显不同。

限于篇幅，本文研究仅考虑了地线自重荷载的影响，实际运行的地线还有可能受到覆冰、大风等极端载荷情况，值得进一步研究。此外，本文研究了地线发生均匀腐蚀的情况，而地线往往还会叠加腐蚀坑等局部不均匀腐蚀情况，有可能导致失效在局部严重位置首先发生。

5 结 论

本文研究了自重荷载作用下腐蚀地线的轴向应力。首先建立了腐蚀地线的非线性有限元模型，随后建立了腐蚀地线的承载力分析计算方法。文中以某实际输电线路的地线为工程背景，研究了自重作用下腐蚀地线的承载力特性，并分析了地线参数和腐蚀参数对其承载力的影响。本文研究表明：地线参数和腐蚀程度对其承载力具有较为显著的影响。弧垂和档距对腐蚀地线的应力影响很大。地线各层股线应力随着弧垂的增大而迅速减小，但各层股线应力随着档距的增加而迅速增加，随着腐蚀面积的增加而小幅增加。同时从分析结果还可以发现，同一层的不同股线，其受力几乎完全一样。在不同的的弧垂、档距和腐蚀面积下，地线各层股线应力由内至外逐渐增加，但腐蚀面积变化引起的应力变化明显比档距和弧垂对股线应力的影响要小很多。不同腐蚀程度下，地线各层之间的应力差基本保持不变，这表明外层地线腐蚀对地线各层中的应力分布影响较小，各层股线应力基本等同变化，这与弧垂参数和档距参数的影响明显不同。