被动拖曳线列阵阵形空间畸变估计算法

滕月慧, 曾 赛



被动拖曳线列阵阵形空间畸变估计算法

滕月慧, 曾 赛

(水声对抗技术重点实验室, 上海, 201108)

拖曳线列阵声呐是远距离探测水下目标的主要装备, 其战术机动会引起拖曳线列阵的阵形畸变, 从而降低拖曳线列阵声呐的空间处理增益, 增大声呐对目标方位估计的误差。基于此, 文中提出了拖曳线列阵的阵形空间畸变的估计方法,利用三维曲线空间投影原理,给出了拖曳线列阵阵形空间畸变的抛物线模型和指数畸变模型的描述方法。结合拖曳线列阵中航向传感器和纵摇传感器的信息,提出了一种强鲁棒性的三维阵形估计算法,并分析了航向传感器中航向角精度和模型失配2个因素对拖曳线列阵阵形估计性能的影响。仿真结果表明: 文中的算法可以估计拖曳线列阵三维阵形畸变,突破了阵形平面畸变和微小畸变的限制。

水下目标探测; 拖曳线列阵; 航向传感器;

0 引言

拖曳线列阵声呐是远距离探测水下目标的主要装备。随着水下目标辐射噪声的降低, 被动声呐的拖曳线列阵越来越长。然而, 拖曳线列阵声呐的战术机动则会引起其拖曳线列阵阵形的畸变, 从而降低拖曳线列阵声呐的空间处理增益, 抵消了长拖曳线列阵声呐的好处, 同时还增大了声呐对目标方位估计的误差。为解决这一问题, 常见的处理方法有以下3种。

1) 自聚焦类。通过阵元接收的信号, 估计阵元的位置, 进而提高波束形成品质, 如特征矢量估计[1], 梯度法[2]以及鲁棒性波束形成算法[3-6]等, 这类算法无需改变拖曳阵结构, 只需增加信号处理单元, 但其计算量极大, 通常对信噪比要求高, 在工程中实现困难, 应用受限。

2) 辅助传感器+流体力学计算方法。通过对拖曳线列阵的受力分析, 建立其在海水中运动模型, 解算阵元位置[7-9]。这类算法需利用阵上非声传感器的输出作为边界条件, 同时需要准确的海流模型和声呐载体的运动学模型, 这2种模型都难以准确描述, 模型失配是其应用的主要阻碍。

3) 辅助传感器类。主要是利用姿态传感器信息或声呐平台机动信息对阵元的位置进行估计[10-11]。这类算法需要在阵中增加姿态类传感器, 其特点是不受目标辐射噪声的信噪比和流体力学模型限制, 在工程上具有可实现性。目前, 工程应用的模型大多基于此类。但一般限制在二维空间中微小阵形畸变, 应用范围有限。

基于以上的认知, 文中按照阵形畸变投影分解思路, 提出了基于抛物线模型和指数畸变模型的阵形空间畸变的描述方法。利用航向角和纵摇角的信息, 提出了一种具有强鲁棒性的三维阵形估计算法，并分析了航向角精度和模型失配因素对阵形参数估计性能的影响。

1 阵形畸变模型分解

建立如图1所示的坐标系, 以第1个声接收阵元为坐标原点(与第1个姿态传感器近似同一位置安装), 以正东方向为轴, 以正北方向为轴, 垂直水平面方向为轴。

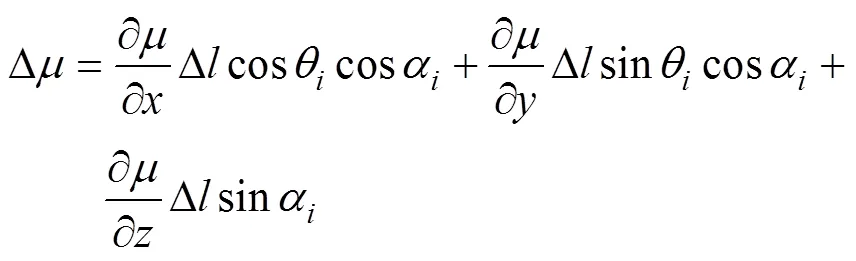
忽略拖曳线列阵在畸变过程中的形变, 故姿态传感器和声传感器间的曲线长度由安装状态决定, 为已知量。所以有

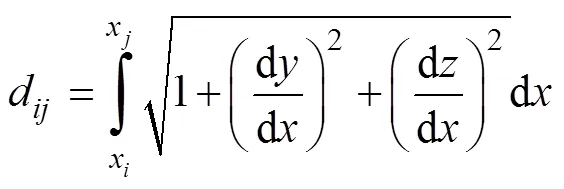
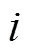
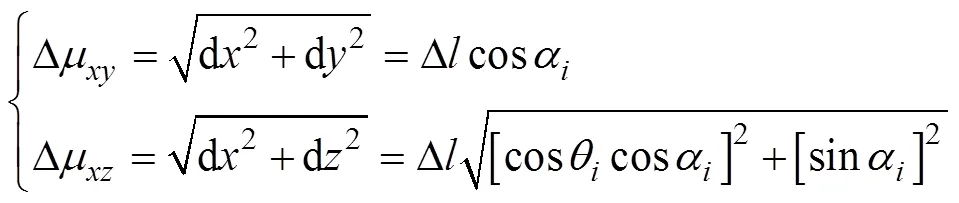
(3)

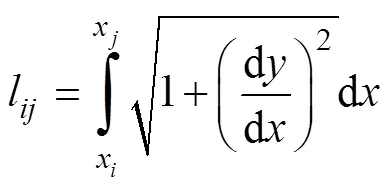
2 畸变阵形参数估计

常用的阵形畸变模型有抛物线模型、高阶多项式和指数模型等。文中研究了抛物线和指数2种模型, 这2种畸变模型是具有解析表达式的模型。

下面以抛物线模型为例, 介绍阵形估计算法。根据图1中的坐标系, 抛物线模型

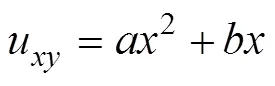
因此，曲线斜率

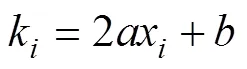
则投影曲线的长度

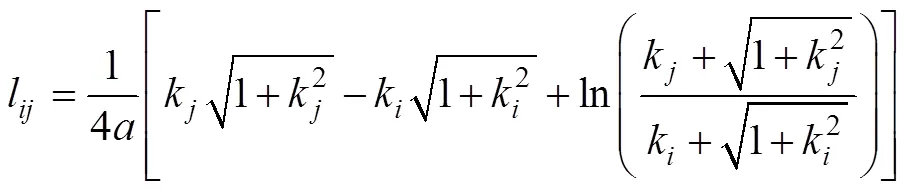
理论上根据式(6)和式(7)可估计出抛物线的2个参数。考虑到传感器的误差, 对抛物线模型的二次项系数采用多次平均法估计

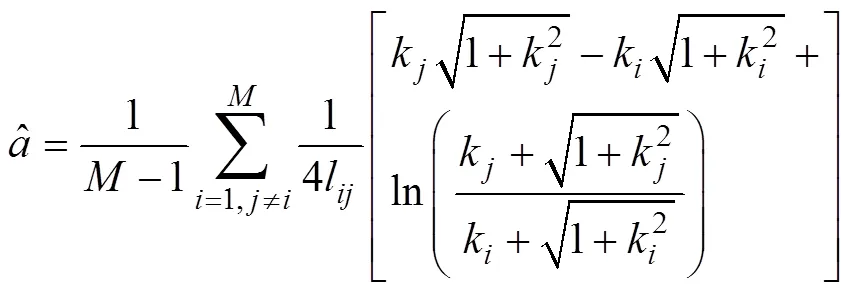
式中,为姿态传感器个数。

根据式(6), 有

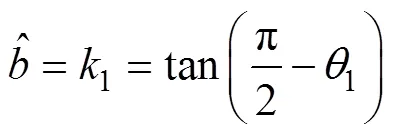
由于航向传感器误差较大, 上述对抛物线一次项系数估计精度较差。针对这一问题, 文中对抛物线模型的一次项系数采用迭代寻优法进行估计, 估计曲线长度与投影曲线长度差可以写成

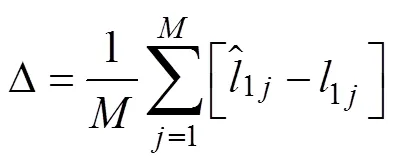
上述模型参数估计方法是针对姿态传感器的误差问题, 提出迭代估计方法, 从而提高参数估计的鲁棒性。

利用同样的思路可以获得指数模型参数的估计方法，其中指数模型可表示为

与式(7)类似，投影曲线的长度

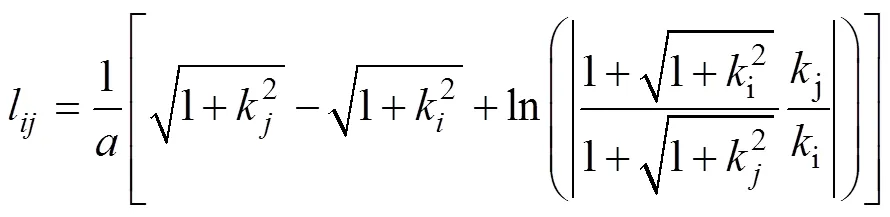
其中投影曲线斜率

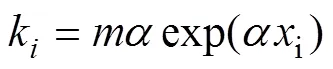
衰减系数用多次平均方法估计, 与抛物线模型中二次项系数估计类似, 修正系数采用与抛物线模型中类似的迭代方法估计。

3 仿真及分析

为了检验上述算法的性能, 采用仿真方法进行验证。模拟目标的运动态势, 如图2所示。

拖曳线列阵的畸变模型为: 水平面内抛物线模型畸变, 垂直面内为指数模型畸变。文中算法可同时处理微小畸变和非微小畸变的阵形参数估计。因微小畸变的限制研究较多，文中关注非微小畸变模型。为了验证文中算法处理三维畸变的效果，选择在垂直和水平面都是非“微小”的畸变模型。这里给出了1种典型的畸变态势,假设阵形畸变模型

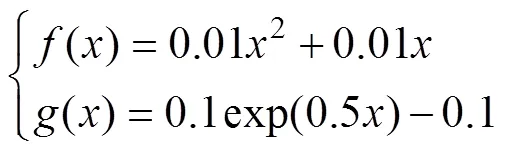
根据畸变模型知: 拖曳线阵在水平方向最大偏移量9.98 m, 垂直方向最大偏移量10.71 m。拖曳线阵接收阵元的位置分布如图3所示, 仿真时为每个航向角均设置了N(0, 2)的随机高斯分布误差, 为每个纵摇角设置了N(0, 1)的随机高斯误差。

利用文中算法获得的阵元位置如图3所示, 可以得出估计位置与实际位置存在偏移, 但阵元的位置偏移要明显小于线阵的假设。这主要是由姿态传感器的输出角度误差引起的, 如果仿真中不加入传感器误差, 两者则可完全吻合。

作为参考, 根据拖曳线列阵阵元实际位置, 进行精确时延补偿后的目标方位历程如图4所示, 目标从0~180°做圆周运动。采用文中算法, 目标的方位历程如图5所示。图4与图5的对比表明: 采用文中算法可以获得目标正确轨迹, 验证了其有效性。图6是在假设拖曳阵元均匀直线分布时的目标方位历程。对比图4和图6, 当拖曳线列阵阵形发生畸变时, 仍按照直线阵处理, 会导致输出波束宽度增加, 增益降低。图7为图4和图6的叠加, 图8为图5和图6的叠加, 表明线阵假设相对文中的阵形估计算法, 估计的目标方位存在较大偏差, 波束形成空间增益亦有损失。

图9为0~180°范围内, 直线阵与阵形估计时输出目标方位偏差。阵形估计方法(图9中用Est.表示)获得目标的轨迹上的方位误差平均值为1°, 标准差为1.4°; 而采用线阵假设方法(图9中用Line表示)获得角度误差平均值为6.9°, 标准差为2.8°。阵形估计相比直线阵假设, 目标方位估计精度提高了6.9倍。

与理想空间增益相比, 图10给出了线阵假设和采用文中提出的阵形估计算法处理这2种状态下的空间增益损失。阵形估计处理后, 拖曳阵空间增益在不同方位上的空间增益损失均值为0.5 dB, 标准差为1.1 dB;而直线阵假设时，其在不同方位上空间增益损失均值为3.2 dB, 标准差为1.9 dB。综上所述，阵形估计相对直线阵假设在方位估计精度和空间处理增益2个方面都有改善。

4 影响阵形畸变估计因素分析

除传感器精度对阵形参数估计存在影响外, 实际影响因素还包括阵形畸变模型失配。下面将针对姿态传感器的精度和阵形畸变模型2个因素进行分析。文中采用阵形畸变估计系数的平均误差作为评估指标。首先, 定义阵元偏移估计系数和阵形畸变估计系数2个量。

假设参考阵元接收到的信号

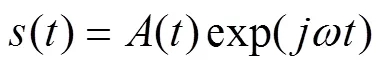
则各阵元接收到声源的信号

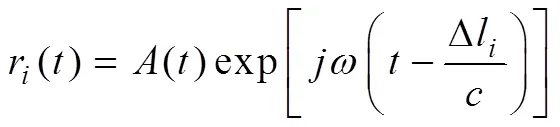
其中

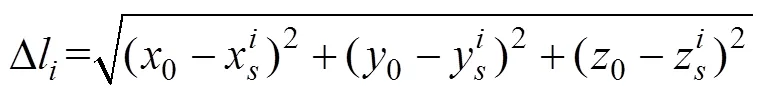
按照估计阵元位置进行修正, 则修正的信号

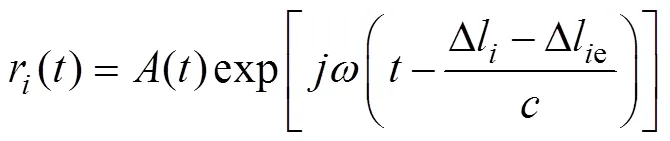
其中

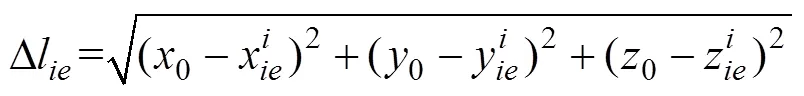
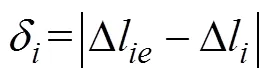
阵形畸变估计系数用阵元偏移估计系数均值表示

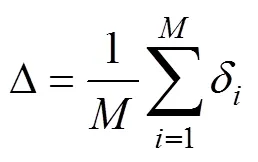
式中,表示阵元的个数。

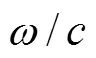
4.1 航向角精度的影响

姿态传感器的输出包括航向角和纵摇角, 根据姿态传感器的特点, 航向角的精度较纵摇角差, 文中在固定纵摇角精度条件下(均方根误差1°), 讨论不同航向角误差的影响。其他仿真条件与第3小节相同, 选择目标处于正横方向时分析。

图11为不同航向角精度时阵元偏移估计系数, 其中黑色实线表示畸变阵形按照直线阵处理时的阵元位置估计误差, 其余分别为航向角精度误差为1°~10°时的阵元位置估计误差, 图中精度误差用“Est: ”后面的数字表示。结果表明, 阵元偏移估计系数与其到参考点的距离有关, 离参考点越远, 估计误差越大。图12为不同航向角精度时阵形估计系数, 结果表明: 航向传感器精度越高, 阵形估计系数越小，方位估计精度越高、空间增益损失越小。

4.2 模型失配的影响

图13为抛物线+指数阵形畸变模型失配成抛物线+抛物线阵形畸变模型时的阵元偏移系数, 其中固定纵摇角精度(均方根误差0.5°)，航向传感器精度设置为1°。说明在航向角精度较高时, 用抛物线模型代替指数模型, 亦可以获得相当高的估计精度。航向传感器的精度是影响阵形估计精度的主要因素, 但随着阵长的增加, 模型失配影响会越来越严重。这可以理解成指数模型展开后在阵的远端需要高阶多项式逼近, 而用抛物线拟合则会使误差增加。但用高阶多项式时存在文中提到的曲线长度无解析解的问题。若采用参数(至少5个, 含积分的上下限和多项式系数)的多维搜索求解稳定最优解, 不但计算量大幅增加, 还存在多维搜索的缺点、局部最优和全局最优问题以及收敛问题, 在工程上实现困难。

5 结束语

文中针对拖曳线列阵阵形畸变导致声呐探测性能下降问题, 研究了拖曳线列阵声呐基于2种畸变模型下的阵形估计算法。给出了基于抛物线模型和指数畸变模型的阵形空间畸变的描述方法。结合航向角和纵摇角的信息, 提出一种具有强鲁棒性的三维阵形估计算法。分析了阵形畸变对目标方位和空间处理增益的影响。通过对不同方位时采用阵形估计算法和直线假设的比较，表明文中提出的算法能够提高波束形成的增益和减小目标方位估计的误差。在仿真条件下, 阵形估计处理相对直线假设空间处理增益提高了2.7 dB, 波束输出的目标方位精度提高了6.9倍。文中提出的算法可估计拖曳线列阵的三维畸变, 突破了平面微小阵形畸变的限制。文中仅采用仿真手段对算法进行了验证, 下一步将开展该算法的试验验证。

[1] 饶伟. 水听器拖曳阵阵形估计方法研究[M]. 北京: 国防科学技术大学, 2007.

[2] 焦君圣. 本舰机动时拖曳阵的阵形估计及左右舷分辨方法[J]. 声学与电子工程, 2007, 88(4): 16-19.

[3] Peter G, William S H, Kuperman W A, et al. Adaptive Be- amforming of a Towed Array During a Turn[J]. IEEE Jou- rnal of Oceanic Engineering, 2003, 28(1): 44-54.

[4] 林鹏, 宫在晓, 郭永刚, 等. 拖曳阵机动时的自适应波束形成[J]. 声学学报, 2013, 38(3): 251-257. Lin Peng, Gong Zai-xia, Guo Yong-gang, et al. Adaptive Beamforming of a Time-varying Towed Array[J]. Acta Acustica, 2013, 38(3): 251-257.

[5] 高守勇, 邱秀分, 申和平, 等. 大孔径光纤拖曳阵阵形畸变对波束零陷的影响[J]. 舰船电子工程, 2016, 36(8): 165-169. Gao Shou-yong, Qiu Xiu-fen, Shen He-ping, et al. Influence of Shape Distortion of Large-aperture Optical Fibre Towed Array on Null-forming[J]. Ship Electronic Engine- ering, 2016, 36(8): 165-169.

[6] 鲁赫, 马启明, 周利生. 大孔径拖线阵阵形畸变问题分析与校正方法研究[J]. 声学与电子工程, 2018, 129(1): 18-21.

[7] 李厚全, 韩树平, 曾广会, 等. 单拖线阵声呐左右舷分辨方法及海试验证[J]. 哈尔滨工程大学学报, 2016, 37 (1): 81-85. Li Hou-quan, Han Shu-ping, Zeng Guang-hui, et al. Dis- crimination Method for the Left and Right Boards Using Towed Linear Array Sonar and Its Verification in an Oce- an Experiment[J]. Journal of Harbin Engineering University, 2016, 37(1): 81-85.

[8] 徐雅南. 高海况下拖曳阵阵形扰动及接收信号特性研究[J]. 舰船电子工程, 2016, 36(4): 146-150. Xu Ya-nan. Array Shape Distortion and Array Signal Cha- racteristics of A Towed Array under Harsh Sea Conditio- ns[J]. Ship Electronic Engineering, 2016, 36(4): 146-150.

[9] Feng Lu, Evangelos Milios, Stergios Stergiopoulos and Amar Dhanantwari, New Towed-Array Shape-Estimation Scheme for Real-Time Sonar Systems[J]. IEEE Journal of Oceanic Engineering, 2003, 28(3): 552-562.

[10] Howard B E., James M S. Calculation of the Shape of a Towed Underwater Acoustic Array[J]. IEEE Journal of Oceanic Engineering, 1992, 17(2): 193-203.

[11] 赵建昕, 孙芹东, 侯文姝. 单深度传感器的矢量拖曳阵阵形估计[J]. 应用声学, 2017, 36(3): 249-257. Zhao Jian-xin, Sun Qin-dong, Hou Wen-shu. The Shape Estimation of Vector Towed Array with Single Depth Se- nsor[J]. Journal of Applied Acoustics, 2017, 36(3): 249- 257.

A Shape Estimation Algorithm of Deformed Towed Array in Passive Sonar

TENG Yue-hui, ZENG Sai

(National Key Laboratory of Science and Technology on Underwater Acoustic Antagonizing, Shanghai 201108, China)

Towed array sonar is the main equipment to detect remote underwater targets. Its tactical maneuver may induce the shape deformation of the towed array, thus reducing the spatial processing gain and increasing the target azimuth estimation error with the towed array sonar. Therefore, a shape deformation estimation method for towed array sonar has been proposed based on parabolic model and exponential model. The shape deformation of the towed array are described by using space projection of three-dimensional curve. Exploiting the information of heading sensor and pitching sensor in the towed array, a three-dimensional array shape estimation algorithm with strong robustness is proposed. The factors of heading precision and model mismatch for the estimation performance of towed array shape parameters are analyzed. It is concluded that three-dimensional towed array shape deformation can be estimated with the presented algorithm, which breaks through the limitation of plane and micro shape deformation in the towed array.

underwater target detection; towed array; heading sensor

TJ630.34; TB566

A

2096-3920 (2018)05-0503-07

10.11993/j.issn.2096-3920.2018.05.020

2016-11-19;

2016-12-18.

滕月慧(1982-),男, 硕士, 高级工程师, 主要研究方向为水声信号处理、水声对抗技术.

滕月慧,曾赛. 被动拖曳线列阵阵形空间畸变估计算法[J]. 水下无人系统学报, 2018, 26(5): 503-309.

(责任编辑: 杨力军)