基于协同探测数据融合的水下多目标跟踪

郭龙祥, 虞涵钧, 生雪莉, 韩 笑, 郝豪言, 陈 洋



基于协同探测数据融合的水下多目标跟踪

郭龙祥, 虞涵钧, 生雪莉*, 韩 笑, 郝豪言, 陈 洋

(1. 哈尔滨工程大学 水声技术重点实验室, 黑龙江 哈尔滨, 150001; 2. 海洋信息获取与安全工信部重点实验室(哈尔滨工程大学), 工业和信息化部, 黑龙江 哈尔滨, 150001; 3. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨, 150001)

在高杂波密度的水下环境中, 若只利用局部传感器来跟踪多个目标, 会产生较高的虚警, 而且跟踪效果受限于传感器本身性能。为此文中基于分布式数据融合模型, 首先在各个无人平台上利用联合概率数据关联(JPDA)形成局部航迹, 然后再用匈牙利算法实现对关联矩阵的最优分配从而达到航迹的实时关联, 最后通过凸组合融合算法形成全局航迹。仿真结果表明, 经过此方法完成的多目标跟踪结果具有更好的可靠性, 其跟踪精度基本在两站跟踪精度之间且具有较低的跟踪误差, 适合在未知基站估计精度的系统中获得更为可信的估计结果。

水下多目标跟踪; 高杂波密度; 分布式数据融合; 联合概率数据关联; 匈牙利算法; 凸组合融合

0 引言

无论是在军用还是民用领域, 水下多目标定位跟踪技术都发挥着重要作用。在军事上, 随着水下竞争日益激烈, 快速而准确地对鱼雷、蛙人、无人航行器等各种水下目标实现跟踪是当下的研究重点; 同时在水下目标打捞, 搜救过程中, 也需要用到水下多目标跟踪技术。相对于雷达探测目标所处的空天环境, 水下环境的复杂性使得声呐探测信号中散射更多, 且因为水下声传播速度较慢, 信号频段更低, 所以获取的目标探测点迹整体上数目偏少, 且其中还包含大量野点, 更加不利于对探测点迹进行定位、跟踪等处理。同时由于受水声时变信道的干扰较大, 信噪比差, 跟踪难度更大[1]。这些问题共同使得在水下完成多目标的跟踪成为了一个较为复杂的任务。

随着信息融合的快速发展, 多传感器目标跟踪问题成了这一领域最活跃的研究之一[2]。利用信息融合来实现水下多目标跟踪有了很大的发展, Bar-Shalom和 Singer 将数据关联技术和Kalman滤波技术有机结合, 使得多目标跟踪技术取得了突破性的进展[3]。随后的一些数据关联算法则在此基础上进一步发展, 针对不同的问题和不一样的侧重点对关联算法进行改进[4-5], 更增进了多目标跟踪技术的适应性。

在多传感器跟踪多目标的系统中, 常常采用集中式和分布式2种数据处理结构[6]。集中式结构是把各传感器的探测数据均发送到融合中心, 在融合中心集中处理。这样的方式能保证数据的完整性, 但对通信链路的要求很高。而分布式结构只把各个传感器处理后数据发送至融合中心, 减少了通信压力, 而且融合中心处理速度能大大提高, 整体的处理能力相对于集中式结构也有提高, 另外还具备更高的容错能力, 不会因为某一个传感器量测错误就极大地影响最后的融合结果[7]。

文中介绍的航迹融合方法是基于分布式的数据融合模型, 如图1所示[8]。考虑到序贯航迹关联算法在杂波密度较高时计算量大且成功关联率不高, 从而改用匈牙利算法实现局部航迹之间的最优分配, 最后因为采用协方差凸组合算法对关联航迹进行融合[9]。

1 局部节点航迹生成

1.1 系统模型

Kalman滤波是一种线性滤波方法, 处理对象是随机信号, 同时运用在时域内, 规避了维纳理论在频域内的问题, 而且在高斯白噪声条件下, 滤波过程能得到最优状态估计。此外又由于Kalman滤波以递归的方式进行的估计, 方便于计算机中实现, 使得Kalman滤波理论被广泛运用于各个领域, 特别在目标跟踪领域获得很大成功。

离散时间系统的状态方程和量测方程可以表示为

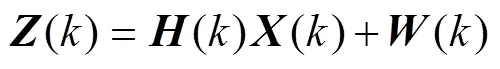
故Kalman滤波系统可以表示为

1) 预测方程

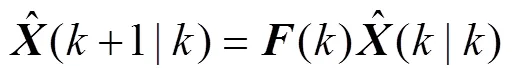
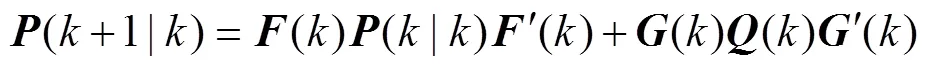
2) 更新方程

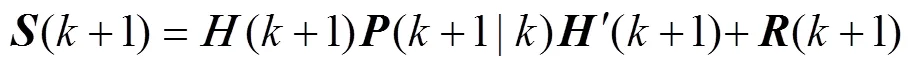
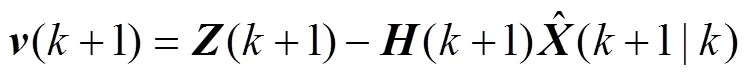
1.2 杂波模型

文中考虑到水下环境的高杂波特性, 故在系统模型的基础上构建服从泊松分布的杂波模型。

根据文献[10]可知二维椭圆波门的面积

虚假量测总数满足

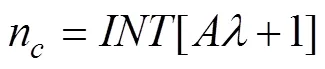
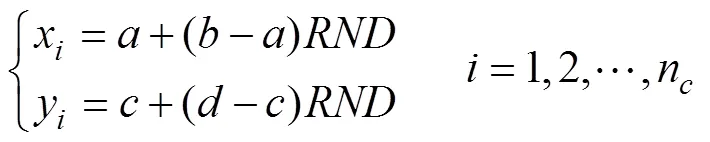
式中:表示在(0, 1)内均匀分布的随机数,

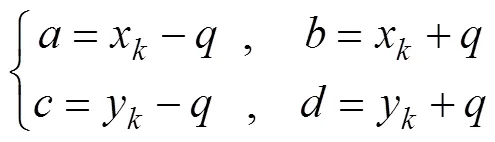
1.3 航迹起始

在未知目标个数的多目标跟踪场景中, 进行数据关联之前需要进行航迹起始[11], 以建立目标档案。修正的逻辑法在虚警概率较高情况下可以快速起始航迹, 故文中采用此方法。

有了归一化距离的限制, 就可以判断当前扫描量测与下一次扫描中的哪一量测互联, 并建立可能航迹, 再用直线外推以关联再下一次扫描中的量测, 以此类推在次扫描时间窗内出现次的量测关联就可以视为成功航迹起始。

1.4 JPDA算法模型

在概率数据互联(probabilistic data association, PDA)算法中, 将落入跟踪门的所有回波都认为是目标的有效回波, 并计算每个回波来自目标的概率, 从而把所有回波的加权和视为等效回波。这样的思路可以用于解决高杂波环境下的单目标跟踪或者是多目标的波门之间不相交的情况。但是当有回波恰好落在了不同目标的波门相交区域, 如何处理这样的回波则受PDA算法的局限了。为此, BarShalom和他的学生[12]在PDA的基础上提出了联合概率数据关联算法(joint probabilistic data association, JPDA), 能够应对高杂波环境下多目标的数据互联问题。

当回波落在不同目标的波门相交区域时, 需要综合考虑回波来自不同目标的概率, 为此在JPDA算法中Bar-Shalom定义了确认矩阵的概念

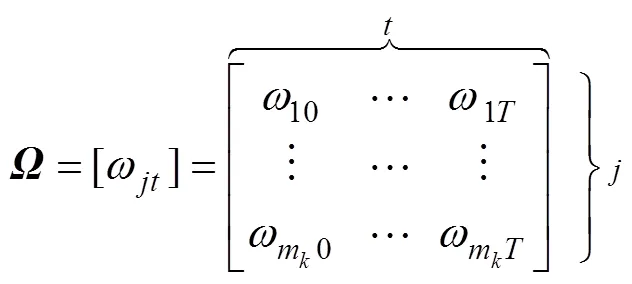
对确认矩阵进行拆分, 得到互联矩阵, 从而一一确认可行互联事件。互联矩阵应满足: 1) 每一个量测有唯一的源; 2) 对于一个给定的目标, 最多有1个量测以其为源。

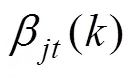
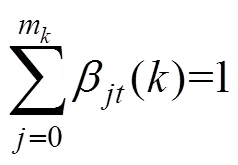
最后得到状态估计及协方差的计算为

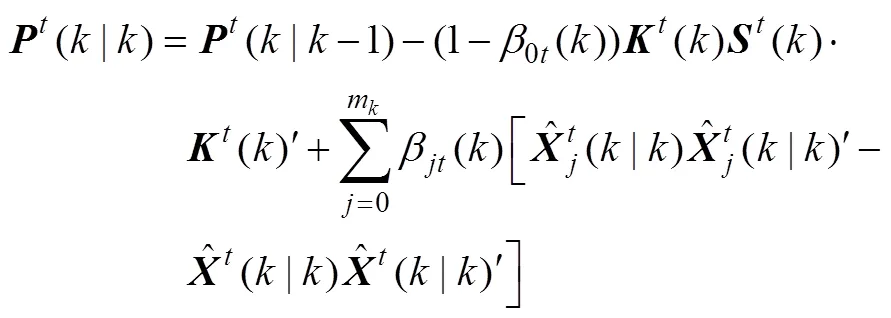
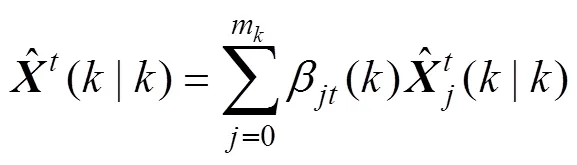
2 航迹融合

2.1 匈牙利算法

匈牙利算法[13](Hungarian algorithm)是一种组合优化算法, 常用于求解指派问题。匈牙利算法的核心思想是如果从成本矩阵的任一行或列的所有项中添加或减去数字, 那么, 所得矩阵的最优分配也是原始矩阵的最优分配。基于此核心思想将航迹关联问题转换成求解航迹矩阵的最优分配问题。匈牙利算法的步骤简单介绍如下。

步骤1: 成本矩阵化简。

1) 遍历矩阵的行, 求得各行的元素最小值, 并对各行上的所有元素减去其最小值。

2) 遍历矩阵的列, 求得各列的元素最小值, 并对各列上的所有元素减去其最小值。

步骤2: 标记0元素操作。

1) 遍历矩阵的行, 若某行存在独立的0元素, 则将该0元素“画圆”, 再遍历该0元素所在的列, 将该列上的其余0元素“画撇”; 若不存在独立0元素, 则暂时越过本行, 处理后面的行。把所有含独立0元素的行操作完毕后, 再回来处理含2个及以上0元素的行, 选择其一0元素“画圆”, 把该0元素所在行的其他0元素和该0元素所在列的其他0元素“画撇”。

2) 遍历矩阵的列, 若某列存在独立的0元素(已经被“画撇”的0元素不看作自由0元素), 再遍历该0元素所在的行, 将该行上的其余0元素“画撇”。若不存在独立0元素, 则暂时越过本列, 处理后面的列。把所有含独立0元素的列操作完毕后, 再回来处理含2个及以上0元素的列, 选择其一0元素“画圆”, 把该0元素所在列的其他0元素和该0元素所在行的其他0元素“画撇”。

3) 重复上述操作, 得到独立0元素(“画圆”的0元素)。

步骤3: 计算独立0元素个数。

1) 如果“画圆”0的个数等于矩阵维数, 那么最优解就是独立0元素所在位置的矩阵原元素, 可直接输出结果。

2) 如果“画圆”0的个数少于矩阵维数, 则继续执行步骤4。

步骤4: 用最少直线经过所有0元素。

1) 对没有“画圆”0元素的行打√号。

2) 对已打√号的行中所有含“画撇”０元素的列打√号。

3) 对打√号列上有“画圆”0元素的行打√号。

4) 重复2)、3)直到得不出新的打√号的行列为止。

5) 对打√号的列画线, 对没打√号的行画线。

这样就能得到经过所有０元素的最少直线集合。

步骤5: 增加(转移)0元素。

1) 求出未被直线经过的元素中的最小值;

2) 对打√行元素减去, 对打√列元素加上;

3) 转到步骤2。

步骤6: 结果输出 。

按照“画圆”0元素的位置, 纪录结果。

将上述步骤用流程图表示, 见图2。

对于2个基站的输出航迹, 计算任意2条航迹之间的检验统计量, 从而构成成本矩阵, 其表示为

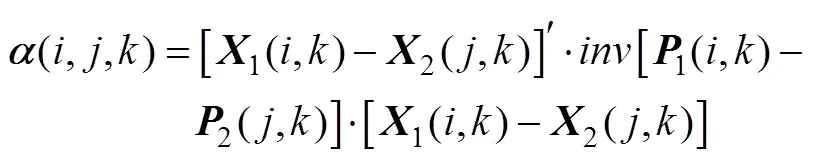
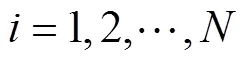
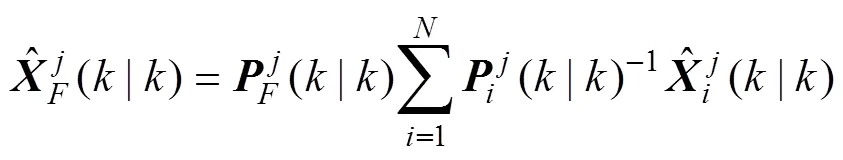
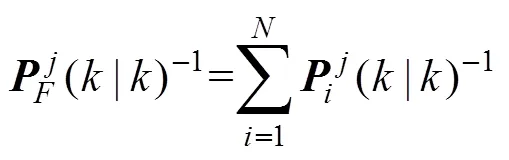
3 仿真结果与分析

文中在水下高杂波密度环境中基于数据融合实现对多个交叉目标的跟踪。采用JPDA算法形成局部航迹, 然后在融合中心利用匈牙利算法实现同属于一个目标的局部航迹关联。最后用凸组合方法融合航迹实现精度更高的多目标轨迹跟踪。

3.1 目标运动模型

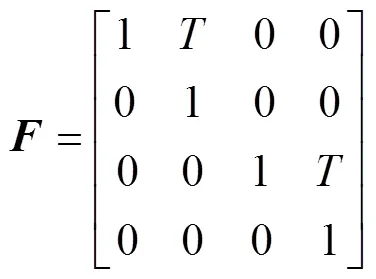
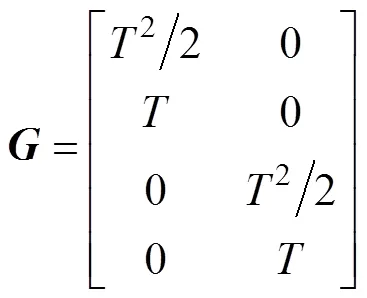
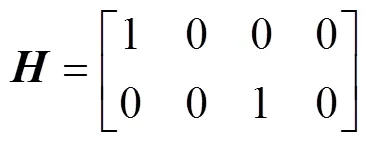
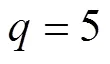
首先设定A、B两基站位置分别为[0, 0]、[0, 1 500], 然后构建3个沿直线运动的目标, 目标初始状态分别为[500, 6, 500, 8]、[500, 6, 1 000, -2]、[500, 6, 700, 8]。在此基础上得到2个基站分别产生的真实目标的量测点(含误差), 如图3中的红色点迹及蓝色点迹, 根据实际轨迹可知, 在采样次数为30、50次左右都有轨迹交叉现象。

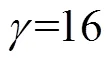
3.2 航迹起始结果

根据1.3节逻辑法航迹起始, 文中取/为3/4,作为正常航迹起始。A、B站的航迹起始以及起始航迹的局部放大结果分别如图5和6所示; 则在表1和表2中表示。而起始航迹所代表的目标初始状态以及由逻辑法起始可能航迹后得到的目标个数以及初始状态, 如表1和表2所示。

3.3 局部节点航迹

根据航迹起始所得到的目标初始状态, 分别对两站进行目标跟踪, 首先以修正的逻辑法起始航迹, 得到航迹初始状态。再运用JPDA生成局部航迹, 其跟踪结果如图7所示, 可见A、B站均能准确跟踪上目标, 且在目标轨迹交叉处没有跟错、跟丢。

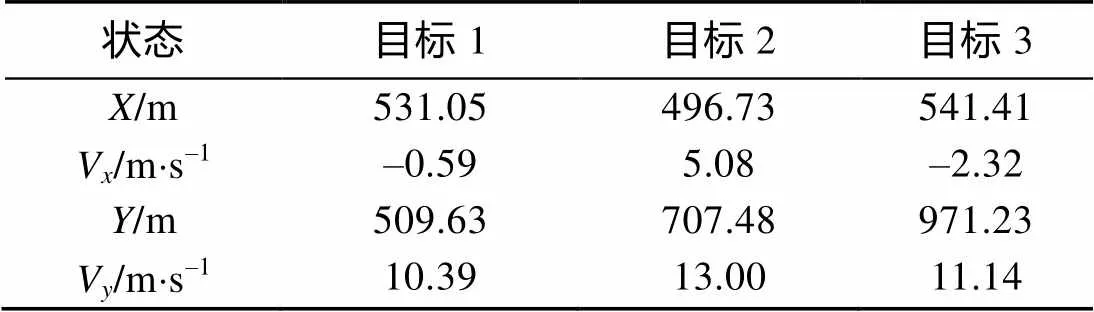
表1 A站起始目标状态

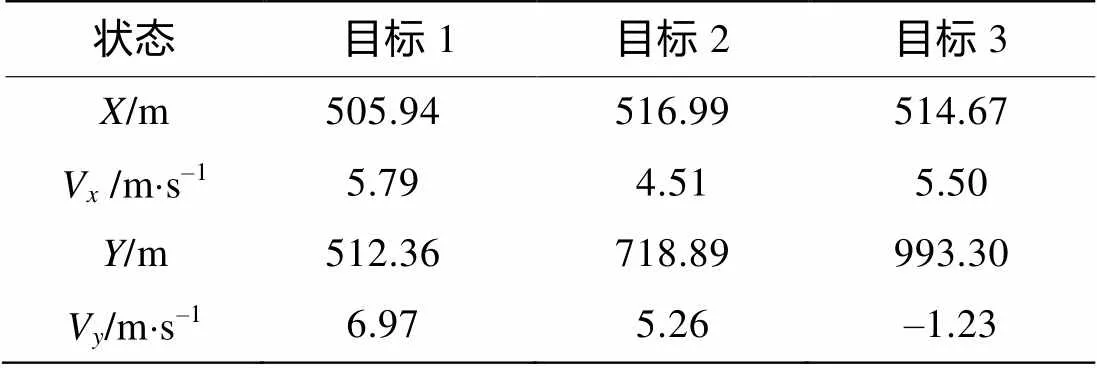
表2 B站起始目标状态

根据位置均方根误差定义

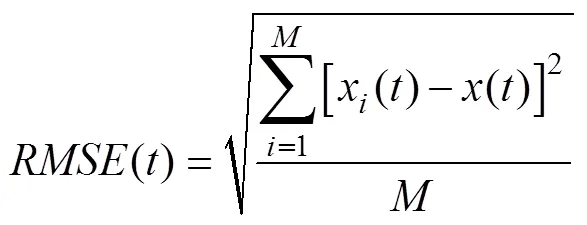
式中,为蒙特卡洛仿真次数。

由上式可得A、B站的轨迹跟踪精度及局部放大结果, 如图8所示。可以看出, 当跟踪轨迹趋于稳定后, A站对3目标的轨迹估计误差分别在42 m、44 m、35 m左右; 而B站对3目标的轨迹估计误差分别在40 m、41 m、25 m左右。

图5 基站A的航迹起始及起局部放大

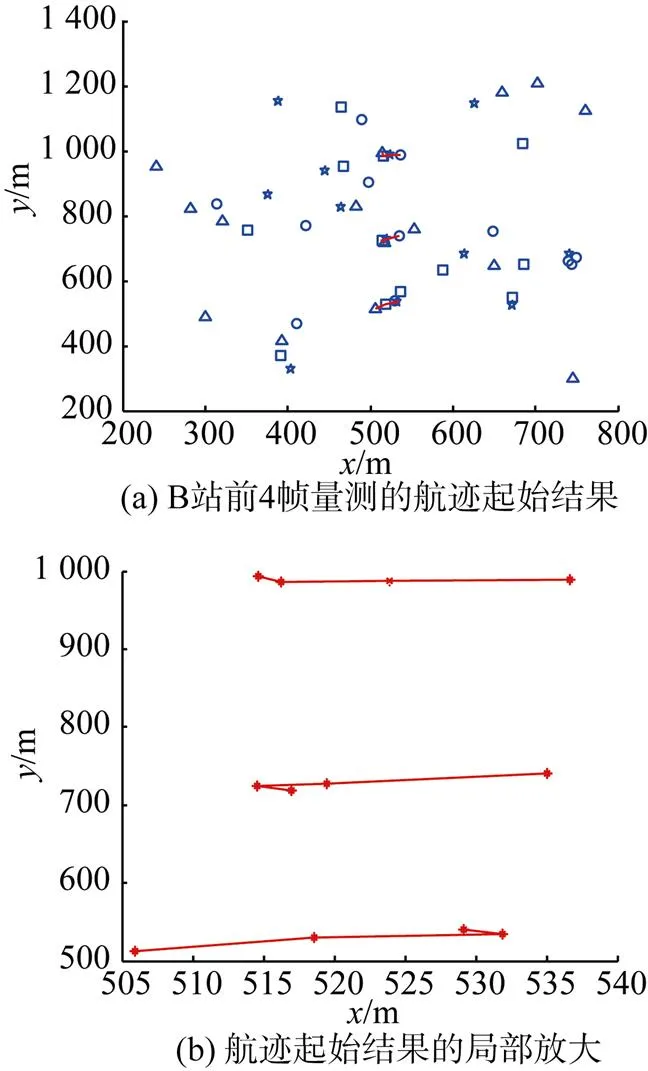
图6 基站B的航迹起始及起始航迹的局部放大

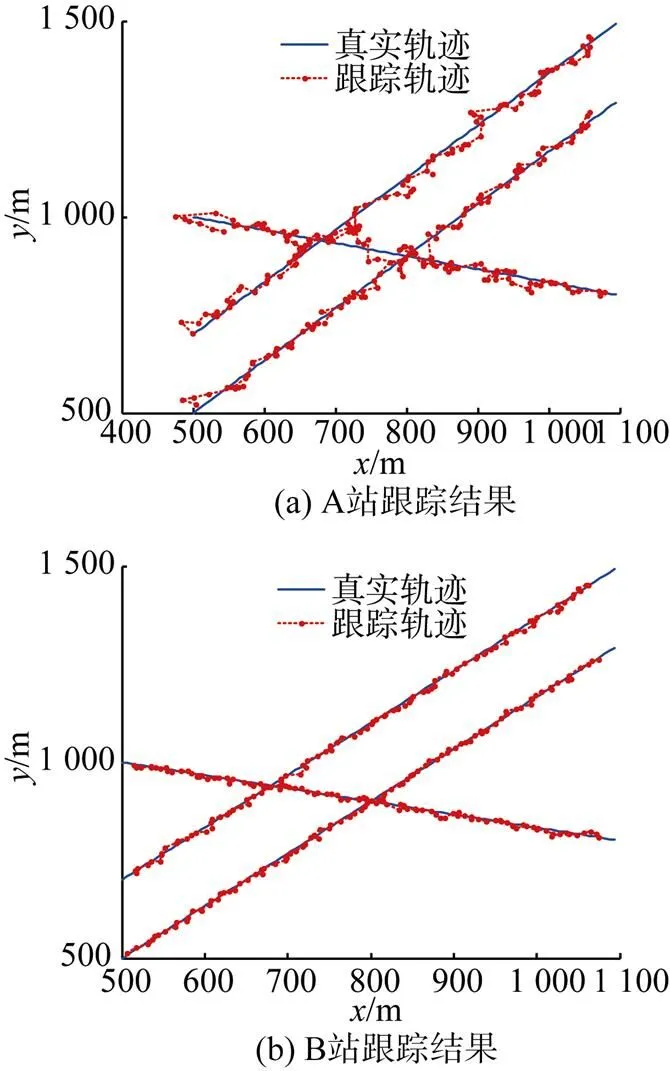
图7 A、B节点局部航迹图

3.4 融合中心航迹融合

在对局部航迹进行融合之前还需经过航迹关联, 把同属于一个目标的航迹归并在一起, 再对其航迹融合才能达到提高目标估计精度的目的,否则未经关联的航迹融合反而会降低估计精度。

由于当航迹数目增多时序贯航迹关联法的计算量增加较大, 为此文中采用了更快速的匈牙利算法, 具体的步骤见2.1节所述。匈牙利算法所需成本矩阵的元素为两站任意2条航迹的检验统计量, 如式(20)所示。据此可以在融合中心得到融合航迹及其估计误差, 如图9和图10所示。由图10可知, A、B站融合后的轨迹对3目标的估计误差分别在41 m、41 m、26 m左右。将融合后的估计误差曲线以及A、B站各自的估计误差曲线按目标分别放在3张图上并显示局部结果, 如图11所示。

通过比较跟踪精度可以清楚地看出, 融合航迹的跟踪误差明显低于跟踪误差较大的基站, 且大部分介于两站之间, 更靠近真实航迹。在不清楚两站跟踪性能或有一站跟踪性能较差的情况下, 可以获取较为准确的估计结果。

4 结束语

文中针对单基地的测量数据运用了JPDA算法, 虽然能够在高杂波环境中跟踪多个运动轨迹交叉的目标, 但是单站跟踪的估计结果比较不稳定, 受限于站址与目标的物理位置以及站址自身的测量精度。基于分布式数据融合模型处理多站测量数据, 仿真结果表明, 对多站局部估计的航迹融合可以在保持较高跟踪精度的同时明显提高目标位置估计的可靠性, 适用于站址测量精度未知且测量值误差较大的水下环境。但是随着目标数目增多以及轨迹复杂性的提高, 关联算法的计算复杂度会影响算法的实时性, 如何降低计算复杂度, 有效完成更高数量复杂目标的跟踪, 将是今后的主要研究方向。

[1] 杨德森, 朱中锐, 田迎泽. 矢量声呐技术理论基础及应用发展趋势[J]. 水下无人系统学报, 2018, 26(3): 185-192.Yang De-sen, Zhu Zhong-rui, Tian Ying-ze. Theoretical Bases and Application Development Trend of Vector Sonar Technology[J]. Journal of Unmanned Undersea Systems, 2018, 26(3): 185-192.

[2] 章飞, 孙睿. 水下多目标跟踪技术综述[J]. 中外船舶科技, 2012(3): 23-29.Zhang Fei, Sun Rui. Overview of Underwater Multi-target Tracking Technology[J]. Chinese and Foreign Ship Science and Technology. 2012(3): 23-29.

[3] Zheng C, Sun D, Cai L, et al. Mobile Node Localization in Underwater Wireless Networks[J]. IEEE Access, 2018, 1(1): 99.

[4] 刘威, 生雪莉, 郭龙祥, 等. 基于m-MHT的主动声呐野点剔除方法研究[J]. 舰船科学技术, 2017, 39(19): 117-121.Liu Wei, Sheng Xue-li, Guo Long-xiang, et al. Research on m-MHT-based Active Sonar Field Culling Method[J]. Ship Science and Technology, 2017, 39 (19) : 117-121.

[5] 陈晓, 李亚安, 蔚婧. 一种海杂波背景下的目标跟踪数据关联方法[J]. 鱼雷技术, 2016, 24(5): 334-339.Chen Xiao, Li Ya-an, Wei Jing. A Method of Target Tracking Data Association in Sea Clutter Background [J]. Torpedo Technology, 2016, 24 (5): 334-339.

[6] 乔向东, 李涛. 多传感器航迹融合综述[J]. 系统工程与电子技术, 2009, 31(2): 245-250.Qiao Xiang-dong, Li Tao. Overview of Multisensor Track Fusion[J]. Systems Engineering and Electronic Technology, 2009, 31 (2): 245-250.

[7] Zhang J, Shi C, Tang K, et al. Research and Implementation on Multi-beacon Aided AUV Integrated Navigation Algorithm[C]//Oceans 2017. Aberdeen: Oceans: 1-5.

[8] 韩崇昭, 朱洪艳, 段战胜. 多源信息融合[M]. 北京: 清华大学出版社, 2006: 257-261.

[9] Julier S. General Decentralized Data Fusion with Covariance Intersection(CI)[M]// Handbook of Multisensor Data Fusion. Boca Raton: CRC Press, 2001.

[10] 何友. 雷达数据处理及应用[M]. 北京: 电子工业出版社, 2006: 84-89.

[11] 汤琦, 黄建国, 杨旭东. 航迹起始算法及性能仿真[J]. 系统仿真学报, 2007, 19(1): 149-152.Tang Qi, Huang Jian-guo, Yang Xu-dong. Track Initiation Algorithm and Performance Simulation[J]. Journal of Systems Simulation, 2007, 19(1): 149-152.

[12] Fortmann T E, Bar-shalom Y, Scheffe M. Sonar Tracking of Multiple Targets Using Joint Probabilistic Data Association[J]. IEEE Journal of Oceanic Engineering, 2003, 8(3): 173-184.

[13] 肖文凯, 肖圣龙, 林华, 等. 基于匈牙利求解的航迹关联算法研究[J]. 舰船电子工程, 2008, 28(10): 137-139, 163.Xiao Wen-kai, Xiao Sheng-long, Lin Hua, et al. Research on Track Correlation Algorithm Based on Hungarian Solution[J]. Ship Electronic Engineering, 2008, 28(10): 137-139, 163.

Underwater Multi-Target Tracking Based on Collaborative Detection Data Fusion

GUO Long-xiang, YU Han-jun, SHENG Xue-li, HAN Xiao, HAO Hao-yan, CHEN Yang

(1. Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001, China; 2. Key Laboratory of Marine Information Acquisition and Security(Harbin Engineering University), Ministry of Industry and Information Technology, Harbin 150001, China; 3. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China)

In the underwater environment with high clutter density, high rate of false alarms will be generated if only local sensors are used to track multiple targets, meanwhile the tracking effect is limited by the performance of the sensors. Therefore, based on the distributed data fusion model, this paper first uses the joint probability data association (JPDA) to form a local track on each unmanned platform, then uses Hungarian algorithm to implement the optimal allocation of the correlation matrix so as to achieve real-time track correlation, finally forms a global track through the convex combination fusion algorithm. Simulation results show that the multi-target tracking results of this method are more reliable, and the tracking accuracy is almost between the tracking accuracy of two stations with smaller tracking error. It is concluded that the present method is suitable for obtaining more reliable estimation results in the system with unknown base station estimation accuracy.

underwater multi-target tracking; high clutter density; distributed data fusion; joint probability data association (JPDA); Hungarian algorithm; convex combination fusion

TJ630.34; TB566

A

2096-3920(2018)05-0387-08

10.11993/j.issn.2096-3920.2018.05.002

2018-07-23;

2018-09-17.

国家自然科学基金(51779061).

*生雪莉(1979-), 女, 博士, 教授, 主要研究方向为水声信号处理.

郭龙祥, 虞涵钧, 生雪莉, 等. 基于协同探测数据融合的水下多目标跟踪[J]. 水下无人系统学报, 2018, 26 (5): 387-394.

(责任编辑: 许 妍)