扭力梁疲劳分析方法研究
2018-11-09荣兵肖攀鞠道杰
荣兵,肖攀,鞠道杰
(中国汽车工程研究院股份有限公司,重庆 401122)
0 引言
由于扭力梁悬架具备结构设计简单、生产及维修成本较低等优点,在中低档乘用车上应用较多。扭力梁的主体结构通常由两边纵臂加中间主梁组成,具有横向稳定杆的作用,主要承受来自路面的扭矩工况。在扭力梁的工程开发设计过程中,需要大量的强度和疲劳仿真分析以及试验来验证其结构性能是否满足设计要求。针对扭力梁的疲劳仿真分析方法已有大量的工程师及学者进行过研究[1-2],疲劳分析基础理论都是基于求解的时域应力历程进行雨流计数和损伤计算,不同点在于时域应力历程的计算方法,由于扭力梁的第一阶固有自由频率通常介于试验场激励载荷的主要集中频段内,常用的时域应力历程计算方法如下:(1)准静态法的应力历程求解,将结构在单位载荷下的静态应力与时域载荷谱进行线性组合得到结构的时域应力历程;(2)模态叠加法的应力历程求解,是通过求解结构的模态频率,在各阶模态频率上进行积分,采用叠加的方式计算得到任意时刻或频域上的应力历程。
文中以某小型SUV后扭力梁为研究对象,采集载荷谱时在扭力梁主梁上布置应变花,测试采集过程中的应变历程。基于虚拟迭代分解的载荷谱采用准静态法和模态叠加法计算测点的应变历程,对实测数据与仿真数据在时域、频域和损伤上进行对比,发现准静态法分析值与实测值更为吻合,其分析精度更高,模态叠加法分析值大于准静态分析值。其次对主梁疲劳进行分析,两种方法的疲劳损伤分布基本一致,损伤区域主要位于主梁中部,模态叠加法损伤值高于准静态法损伤值,进一步验证扭力梁疲劳分析时模态叠加法偏于保守。
1 扭力梁激励载荷获取及分析
1.1 激励载荷谱获取
在新车型的开发中,结构件的疲劳性能验证基本以整车道路试验为基础,故在新车型开发过程中基于路试载荷谱进行结构件疲劳仿真分析,对指导结构设计优化就显得尤为重要。由此可见,获取精确的路试动态载荷是疲劳研究的基础和关键,考虑到对分析精度的对比,采集信号除去常用载荷分解所需信号外,在扭力梁主梁的左、中、右区域各布置一个应变花,测试采集过程中的时域应变历程,用于后期仿真分析的对标数据。扭力梁上应变花具体布置详见图1。

图1 测试应变花布置
路试载荷谱的采集计划依据该车型在国内某试验场的强化路试规范制定,采集区域包括强化路面区与性能路面区,强化路面区采集轨迹如图2所示,该区域激励载荷主要来源于路面的凹凸起伏,性能路面区域主要进行制动操作,载荷来源于驾驶员操控。
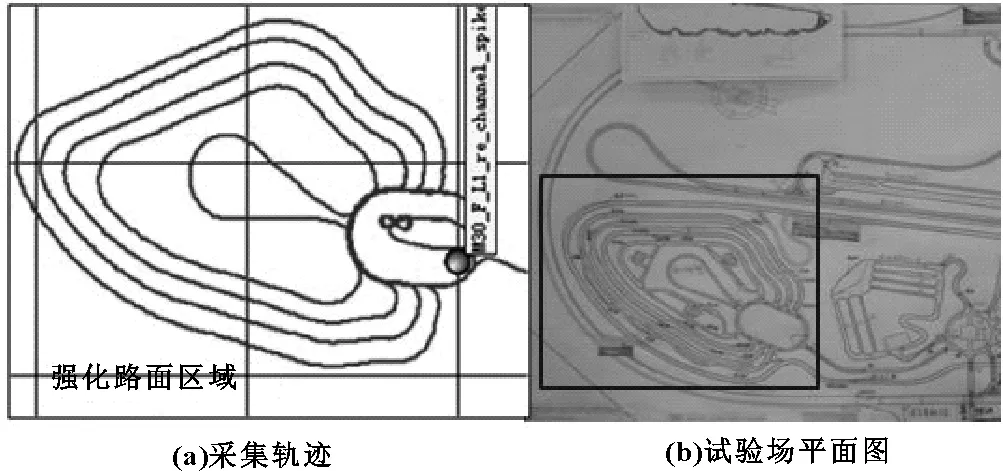
图2 强化路面区域采集轨迹
1.2 激励载荷谱分析
针对采集的载荷原始谱,为保证采集数据的准确性,以及合理压缩数据,通常会对数据进行毛刺漂移检查及去除、特殊路面工况识别及分割、有效样本筛选等工作,详细处理过程可参考文献[3-5]。由于文中主要对扭力梁疲劳分析方法进行研究,在此不再赘述。依据路试规范最终整理得到强化区域16个特殊路面载荷谱,以及性能路面区域3个制动工况载荷谱,详见表1。
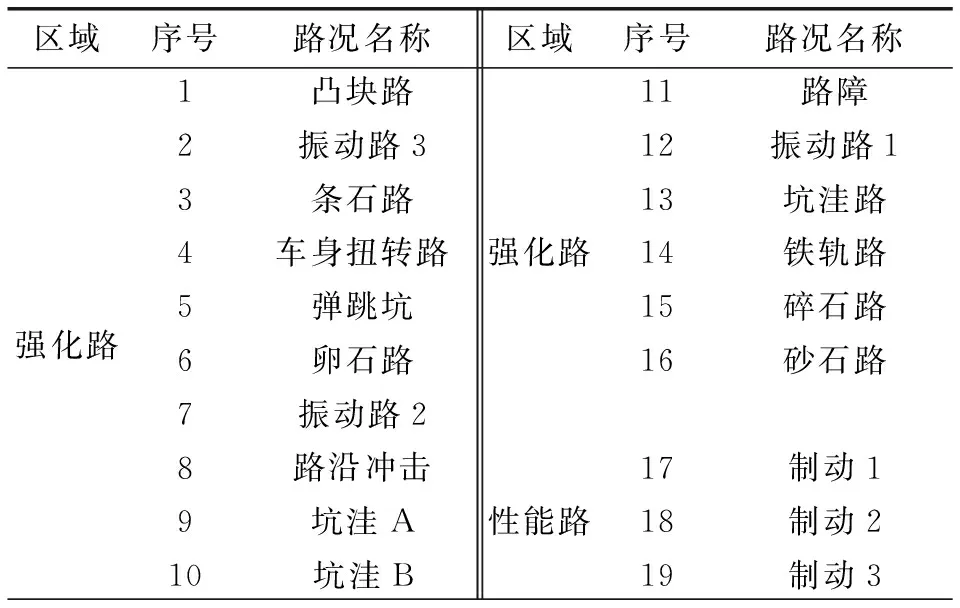
表1 试验场采集工况
由于激励载荷的频率成分的不同,不同疲劳分析方法的结果也存在一定的差异,对扭力梁的激励载荷进行频谱分析,可了解激励频段与结构固有模态频率之间的关系。同时为减少后期对比分析的工作量,拟采用某一工况进行对比,要求该工况的激励频段能全面覆盖试验场所有激励的频段,从而保证该工况分析结论与整个试验场工况分析结论一致。整合筛选所有工况载荷谱,对其中右后轮心在X、Y、Z3个方向的力进行频谱分析,发现卵石路工况与所有路面频域成分基本一致。扭力梁右轮心FX载荷主要集中频段均在10~20 Hz和30~35 Hz,详见图3;FY载荷主要集中频段均在10 Hz附近和20~30 Hz附近,详见图4;FZ载荷主要集中频段均在8~25 Hz,详见图5;综上,3个方向激励频段均一致,故选择卵石路载荷谱作为应变历程对比工况。其次,基于整车多体动力学模型,采用虚拟迭代方法进行采集工况的载荷分解[5],得到扭力梁8个接口点上48个通道的信号,以便于后期扭力梁主梁的疲劳分析和对比。

图3 右后轮FX频谱对比
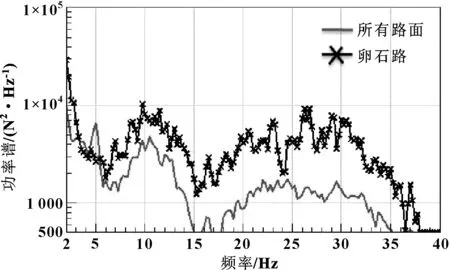
图4 右后轮FY频谱对比
2 扭力梁测点应变分析及对比
在仿真分析中建立准确、恰当的有限元模型至关重要。针对不同的分析类型,模型建立的侧重点不同。应在保证计算结果精度的前提下,尽量缩短建模时间和CPU的运算时间。为了准确模拟计算扭力梁的应变历程,有限元建模时单元网格平均尺寸为5 mm,保证三角形单元比低于5%。为便于虚拟应变片与真实应变片数据进行对比,在建模时,按照应变花布置位置和方向划分单元网格。扭力梁主梁虚拟应变片设置详见图6。

图6 有限元模型及虚拟应变片设置
对该车型扭力梁进行自由模态分析,获得前5阶自由固有模态参数如表2所示,第一阶频率为20.13 Hz,其振型为扭力梁整体的扭转变形,试验场的载荷激励主要集中在40 Hz以下(见图3—图5),由此可见,扭力梁第一阶固有自由频率介于试验场载荷主要激励频段0~40 Hz内。故文中采用准静态法与模态叠加法进行扭力梁的虚拟应变历程计算,并通过与实测应变历程的对比,分析两种方法的准确性。
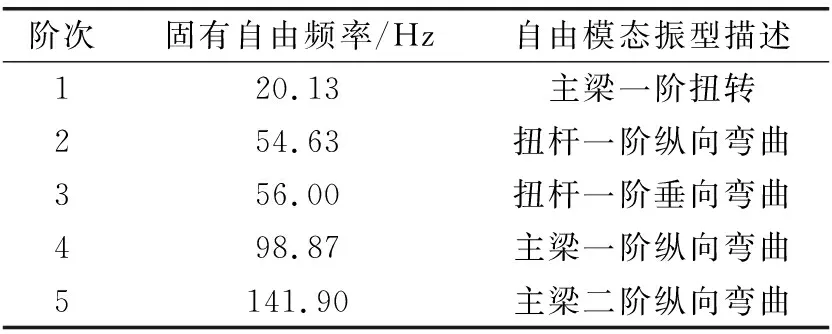
表2 扭力梁自由模态信息
准静态法的应变和应力历程求解是在结构各受力方向施加单位载荷,分别计算各单位载荷分量的结构静态应变和应力,再将其与动载时间历程相乘叠加求和,即得到结构的应变和应力历程。
基于结构件各接口点时域载荷谱可进行时域瞬态动力学分析,计算应变和应力历程,但由于该计算效率极低,且对计算机性能要求较高,故采用模态叠加法来缩减动力学方程的自由度。缩减后可以获得各阶模态主坐标时间历程,再结合各阶模态应变和应力信号,计算结构的动态应变和应力历程。
利用上述两种方法,基于扭力梁的卵石路分解载荷计算主梁对应测点的虚拟应变历程,结合实测的主梁应变历程,可判断两种计算方法的准确性。主梁上共布置3个应变花,测量应变数据9组,将3个应变花中应变最大的数据进行对比,时域上准静态法分析值的幅值范围与实测值更为吻合,而模态叠加法数据在局部时段存在一定的振荡现象,详见图7—图9;频域上,模态叠加法在扭力梁第一阶固有自由频率附近产生一个较大的能量贡献,与实测数据不相符合,详见图10—图12。综上可知准静态法的精度较高,模态叠加法分析法精度较差,且结果偏于保守。

图7 左应变花90°应变时域对比

图8 中应变花45°应变时域对比

图9 右应变花90°应变时域对比

图10 左应变花90°应变频域对比

图11 中应变花45°应变频域对比

图12 右应变花90°应变频域对比
利用标准S-N曲线计算9组应变伪损伤值如表3所示,将实测与仿真对应的3列数据作为3个样本,按照多元素样本求模原则[4],以实测样本为基准损伤向量,对此向量各单元进行归一化处理,其余向量各单元为与该向量对应单元的比值,按向量模求解方式求解出各样本的累积损伤模,再以实测数据为基础,计算出两仿真数据与之比例见表4,准静态法为实测数据的148.44%,模态叠加法为其764.48%。由此进一步验证了准静态法的精度更高,与实测更加吻合。

表3 应变伪损伤

表4 应变伪损伤向量模及占比
针对主梁测点上模态叠加法仿真数据在扭力梁第一阶固有自由频率附近功率谱远高于实测数据的问题,可从扭力梁的自由模态与工作模态进行对比分析。在进行各阶模态主坐标时间历程计算时,扭力梁处于自由状态,并采用惯性释放的方法进行瞬态动力学分析,而外部激励频率覆盖了扭力梁第一阶固有自由频率20.13 Hz,引起结构的拍振形象,故应变形成振荡,与实测不符。扭力的工作模态是处理装配状态下的,与车身通过左右衬套、螺旋弹簧和减振器进行装配,按装配关系简单建立扭力梁装配状态的有限元模型,在仅考虑车身衬套、螺旋弹簧刚度及预载情况下,计算出扭力梁的装配模态频率如表5所示,主梁扭转频率提升到76.17 Hz,大于激励载荷的覆盖频段,故在实际工作装配下,结构不会产生拍振形象,所以在实测应变数据的频域分析中,扭力梁第一阶固有自由频率附近不会存在较大的贡献量。
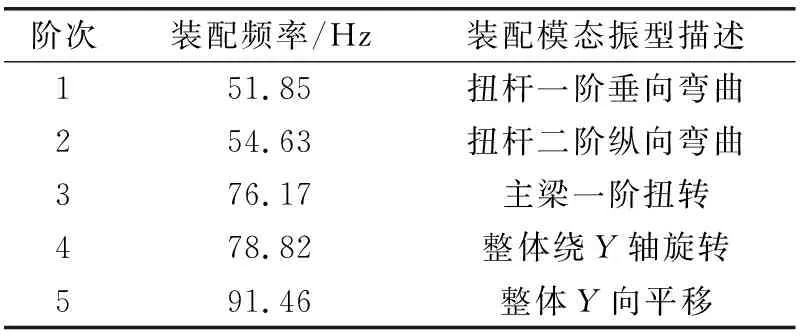
表5 扭力梁装配模态信息
3 扭力梁疲劳分析及对比
将所有工况的扭力梁分解载荷,按照该车型试验场强化路试规范进行组合,分别采用准静态法和模态叠加法进行扭力梁主梁的疲劳仿真分析,主梁材料抗拉强度为454 MPa,屈服强度为289 MPa。两种方法计算的主梁疲劳损伤云图如图13—图14所示,其中准静态法最大损伤值为2.22×10-2,模态叠加法最大损伤值为5.23×10-2,为准静态法分析结果的2.36倍;两种方法计算损伤分布基本一致,损伤区域主要位于主梁中部;模态叠加法损伤值明显高于准静态法损伤值。
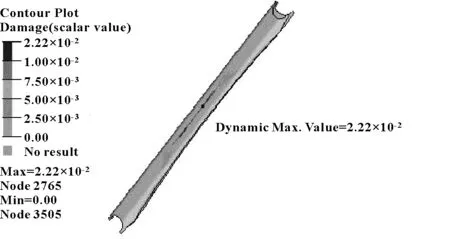
图13 基于准静态法的损伤云图
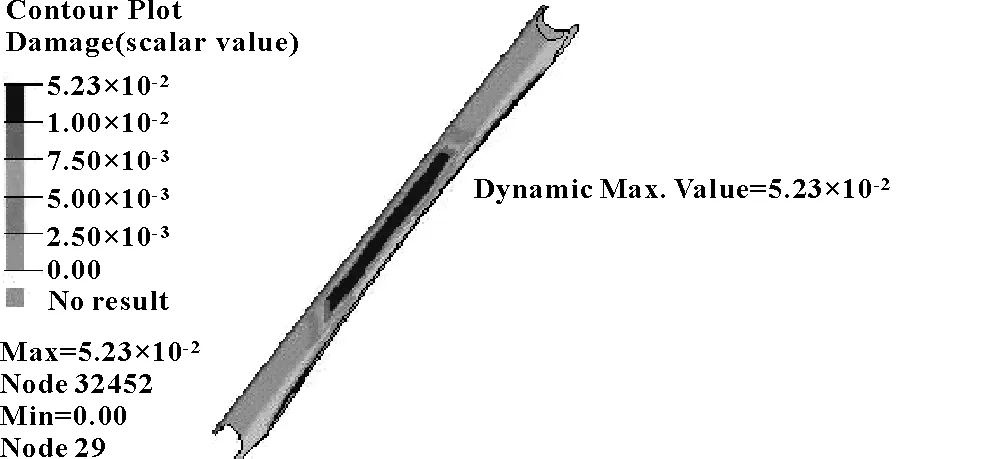
图14 基于模态叠加法的损伤云图
从两种疲劳分析结果中提取应变片测点的仿真损伤值详见表6,模态叠加法分析值均大于准静态法分析值,从而进一步验证了应变历程对比分析的结论。

表6 应变片测点仿真损伤对比
4 结论
扭力梁作为中低端乘用车后悬架系统中常用的一种部件,与其他底盘部件存在一定的差异,其一靠自身结构的变形来实现悬架的运动形式,其二扭力梁的自由模态相比其他部件较低。由于通常路面激励频率会覆盖扭力梁的第一阶自由模态频率,故文中以扭力梁主梁上实测应变历程为基础,分别采用准静态法和模态叠加法计算测点的应变历程,对实测数据与仿真数据的时域、频域和损伤对比分析,发现准静态法分析值与实测值更为吻合,分析精度更高,模态叠加法分析值大于准静态法分析值,结果偏于保守;同时将扭力梁的自由模态与工作模态进行对比,可知工作模态下扭力梁扭转模态频率得到了大幅提升,合理解释了在实测应变数据的频谱分析中,扭力梁第一阶固有自由频率附近不会存在较大的贡献量,则基于准静态法的疲劳分析方法更适用于扭力梁。
在车辆的设计验证过程中,工程师都会确保底盘各部件在实际的使用过程中不会产生共振形象。如果在整车运行过程中,扭力梁产生了共振形象,基于准静态法的疲劳分析就不再适用。
