例谈整体思想在数列中的应用

魏建平

(甘肃省礼县第二中学 742201)

例1 已知{an}为等比数列，且an>0，a2a4+2a3a5+a4a6=25，那么a3+a5=___.

分析要求a3+a5的值，通常是先求出数列的首项a1和公比q，而由题目的条件无法解出确定的a1和q，但若把a3+a5看成一个整体，此题就可以迎刃而解.

例2 一个等差数列的前12项和为354，前12项中偶数项和与奇数项和之比为32∶27，求公差d

分析此题若用前n项和公式建立方程组显然运算量大，而用等差数列的性质，整体代入则可简化计算.

例3 已知数列{an}的前n项和Sn=2n2-3n+1，求a4+a5+a6+a7+a8+a9+a10的值.

分析注意到a4+a5+a6+a7+a8+a9+a10=S10-S3，由此整体算出a4+a5+a6+a7+a8+a9+a10的值.

解因为Sn=2n2-3n+1，所以S10=2×102-3×10+1=171，S3=2×32-3×3+1=10.所以a4+a5+a6+a7+a8+a9+a10=S10-S3=161.

例4 在各项均为正数的等比数列{an}中，已知a1·a2·a3·…·a24=248，求log2a2+log2a5+log2a8+…+log2a23的值.

分析如果求出a1和q，则问题极易求解，但求a1和q需要两个方程，而已知中仅有一个方程，因此可考虑将a1与q作为一个整体解出，然后再整体代入即可.

分析一利用等差数列求和公式，整体求出100a1，再求和.

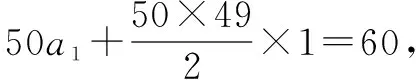
分析二根据等差数列的性质，联系未知与已知，应用整体思想将a1+a2+…+a99当做一个整体来考虑.