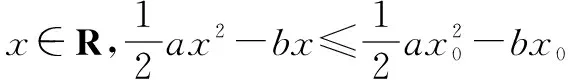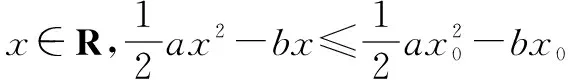盘点高考中的二次函数

付一骏

(河南省民权县高级中学 476800)

一、二次函数的图象

整合二次函数的图象信息通常有以下几点:开口方向(向上或向下)、对称轴的位置、顶点(特别是与坐标轴的交点)坐标、最值的大小等.

例1 设abc>0,二次函数f(x)=ax2+bx+c的图象可能是( ).

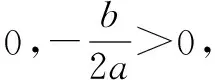
二、二次函数的定义域

二次函数的定义域是一个自变量的取值区间,对于值域等性质的影响也是客观存在的,不可小视.

A.-2 B.-4 D.-8 D.不能确定

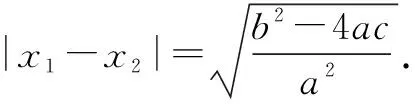
三、二次函数的值域

值域要在单调区间,以及对称轴,相应的定义域内结合图象来分析.

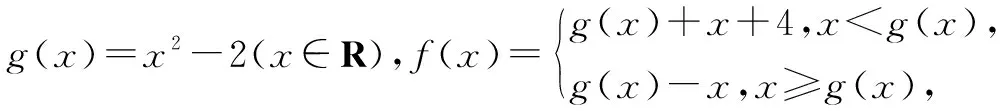
四、二次函数的解析式

二次函数的对应法则有顶点式、零点式、一般式等三种,注意三者之间的相互转化.

例4 若f(x)和g(x)都是定义在实数集R上的函数,且方程xf[g(x)]=0有实数解,则g[f(x)]不可能是( ).

解设x0为方程x-f[g(x)]=0的一个实根,则f[g(x0)]=x0.设g(x0)=y0,则f(y0)=x0,所以g(x0)=g[f(y0)]=y0,即g[f(y0)]-y0=0.这说明方程x-f[g(x)]=0至少有一个实根y0,于是有结论:定义在R上的函数f(x)与g(x),若x0是方程f[g(x)]=x的实数解,则g(x0)必是方程g[f(x)]=x的实数解.

五、二次函数的零点

一般情况下,可通过画函数图象、判断特殊点的函数值的情况,布列不等式(组)来解决问题.

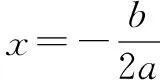
A. {1,2} B. {1,4}

C. {1,2,3,4} D. {1,4,16,64}

六、二次函数的最值

二次函数的最大值和最小值一般在对应图象的顶点或区间端点处取得.因此,关于对称轴与区间的相互位置关系的讨论往往成为解决二次函数在闭区间上的最值问题的关键,通常需要考察“一轴四点”,即对称轴、顶点、区间两端点和区间中点.

例6 已知a>0,则x0满足关于x的方程ax=b的充要条件是( ).