浅谈高中数学中三角函数学习心得

张芷若

(江苏省丰县中学高二 221700)

在高中数学学习的过程中，三角函数作为主要的学习内容，其运算的方式比较灵活，并且知识的理论性强.因此，在实际的学习过程中，运用三角函数知识解决相关的问题，减少运算量，并且培养高中学生的解题能力，有利于我们学生的创新发展.三角函数也是高考中的重要内容，是高等数学学习的基础，因此，掌握高中三角函数知识内容，提升学生的高考成绩，对学生的未来学习有着重要意义.

一、注重三角函数基础知识和概念的学习

三角函数知识内容，有不少的概念和理论等基础知识.作为学生应当牢牢掌握基本的概念和理论，为接下来的深层次学习，奠定良好的基础.对于高中学生来说，正弦函数和余弦函数等相关的基本知识和概念，在初中阶段已经接触和学习，因此，在学习的过程中，学生不需要花费过多的时间，重点学习的内容应当是三角函数的相关定理和变形公式.

因此，在学习的过程中，我们首先要认识和理解三角函数的基本概念，这些内容可以通过相关的图象，进行相应的辨识和了解，在三角函数了解的过程中，可以适当了解一下圆的含义.针对不同的三角函数，应当理解其图象的变化性质，函数不同，图象存在很大的差异，但相互之间存在一定的联系，作为学生应当牢牢掌握.

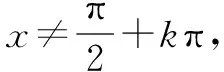
同时，还需要学习相关的变形公式，如两角和与差公式、和差化积公式、二倍角公式等等.针对这些变形公式，学生需要牢记其变化关系，同时要深入地了解其变化的过程，明白其变化的原理，为以后的学习奠定良好的知识基础.

二、注重课前预习和课后复习的开展

数学学习的过程中，通过观察身边同学的学习情况，发现不少的学生在学习之前，没有开展预习的习惯，并且在课堂结束之后，没有进行有效的复习，巩固课堂知识内容.在学习的过程中，没有对将要学习的内容进行相应的预习，导致课堂学习跟不上老师的节奏，部分学生在课后复习时，过分注重习题的解答，复习缺乏重点，导致三角函数的学习出现短板.

所以，在高中数学三角函数学习的过程中，我们需要做好预习和复习.在课前预习时，新课内容的提前预习是一部分内容，同时学生需要对上节课内容进行回顾.根据数学知识内容的安排来说，前后两节课程的知识点是相互联系的，三角函数的知识内容也是如此.

如，在余弦函数学习之前，先学习的是正弦函数，余弦函数的相关知识预习时，学生需要注意正弦函数相关知识的回顾，在回顾的基础上，开展余弦函数的预习学习.针对学生课后复习来说，练习题训练这样的方式并不能取得良好的复习效果.

在课后复习的过程中，需要按照相应的复习顺序开展复习.第一步，针对学习过的知识内容，开展回顾梳理活动，对相关的方法、原理等内容进行归纳和总结，确保其清晰明确.第二步，结合针对性的练习题目，采取有效的解题分析，并且理解题目中所要考察的相关知识点和内容，并且明确三角函数相关知识在题目中的应用，如何运用，问题如何解答.第三步，结合学生的题目解答过程中，学生应当分析和总结，将其中的理论知识升华为具体的解题思路和模式，形成符合自身特点的学习方式，有效提高学习的复习效率.

三、加强一题多解训练，提高自身解题能力

高中数学三角函数的学习，一题多解是多数学生关注的问题.不少的三角函数题目，在实际的解题过程中，其方式和方法不止一种，可以从不同的角度入手，实现问题的有效解答.高中阶段的学生，应当具有一题多解的思想和能力.在高考的过程中，一些出题者，针对三角函数问题，其常规的解题思路中，设置相应的解题障碍，隐藏一些解题的技巧和途径.如果学生在解题时，不具备一题多解的思想，在常规解题方式受到阻碍，无法寻找其他解题方式时，就会出现无法解题或者解题错误，最终影响我们的考试成绩.所以，在日常的学习中，应当注重一题多解方式的思想和训练.

例题(2016江苏 数学)在锐角三角形ABC中，如果sinA=2sinBsinC，那么tanAtanBtanC的最小值是____？

解法1 根据已知sinA=2sinBsinC，可以转化成sinBcosC+cosBsinC=2sinBsinC，所以tanB+tanC=2tanBtanC.

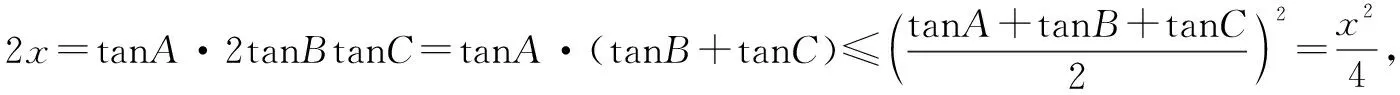
在解题的过程中，除了上述的三种解题方式，还可以利用其它的方式完成解题.作为学生，在学习的过程中，应当不断思考，促进自身解题能力的提高，能够更好地掌握三角函数知识，提高课堂学习的效率，取得良好的考试成绩.

高中阶段的学习中，三角函数作为重要的学习内容，在学习的过程中，存在一定的难度.因此，学习时，应当掌握一定的学习技巧，促进自身学习能力和水平的提升.结合实际的学习过程，经过相应的归纳和总结，可以得出以下几点经验和心得.首先，学习时，需要掌握三角函数相关的基础知识、原理和概念，牢固的掌握.其次，学习的过程中，注重课前预习和课后复习的开展.最后，加强一题多解的习题训练，学好三角函数.