立体几何中的翻折问题
2018-11-08莫碧华
莫碧华
(重庆市第三十七中学校 400084)
立体几何的翻折问题是指将一平面图形翻折后变成空间图形,然后根据平面图形的数量关系、位置关系等来研究空间图形中各元素间的数量关系、位置关系等问题.解决翻折问题的关键是确定翻折前后的不变量与改变量.在解题时仔细审视从平面图形到立体图形的几何特征的变化情况.
一、翻折中的线面位置关系的判定
通过平面图形的翻折后变成空间图形,进而研究翻折后的空间图形中的点、线、面的位置关系,判定相关的点、线、面的平行或垂直关系等.
例1 如图,以等腰直角△ABC的斜边BC上的高AD为折痕,把△ABD和△ACD翻折成互相垂直的两个平面后,某学生得出下列四个结论:
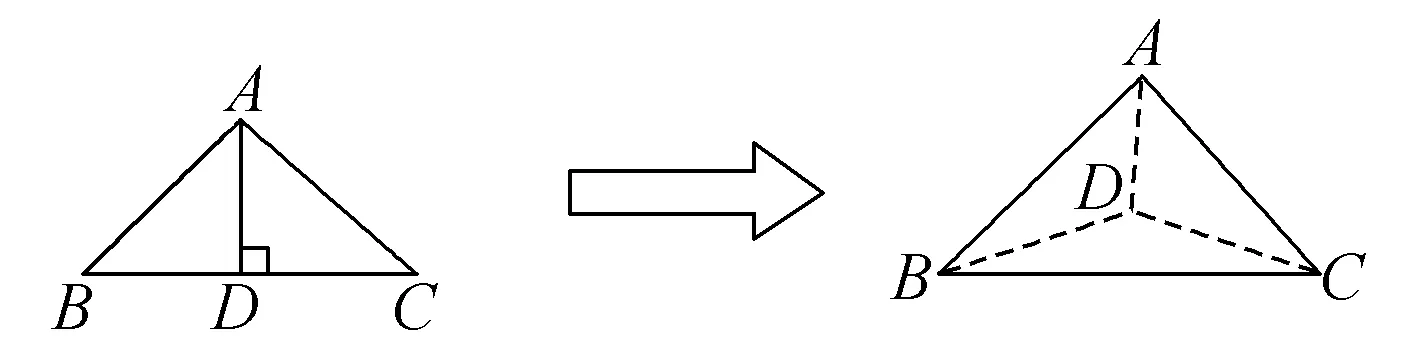
①AB⊥CD;
②△BAC是等边三角形;
③三棱锥D—ABC是正三棱锥;
④平面ABD⊥平面ABC;
其中正确的是____.(写出所有正确命题的序号)
解析由题知,CD⊥平面ABD,故CD⊥AB,①正确;AD为等腰直角△ABC的斜边BC上的高,平面ABD⊥平面ACD,则AB=AC=BC,△BAC是等边三角形,②正确;易知DA=DB=DC,又由②知③正确;由①知④错.故填:①②③.
点评涉及翻折中的线面位置关系的判定,根据翻折前后所对应的平面图形与空间图形的位置关系,判定线线、线面、面面的平行、垂直等位置关系.
二、翻折中的数量关系的证明与计算
通过平面图形的翻折后变成空间图形,可以用来解决空间几何体的表面积与体积,空间角,空间距离等数量关系的证明与计算等.
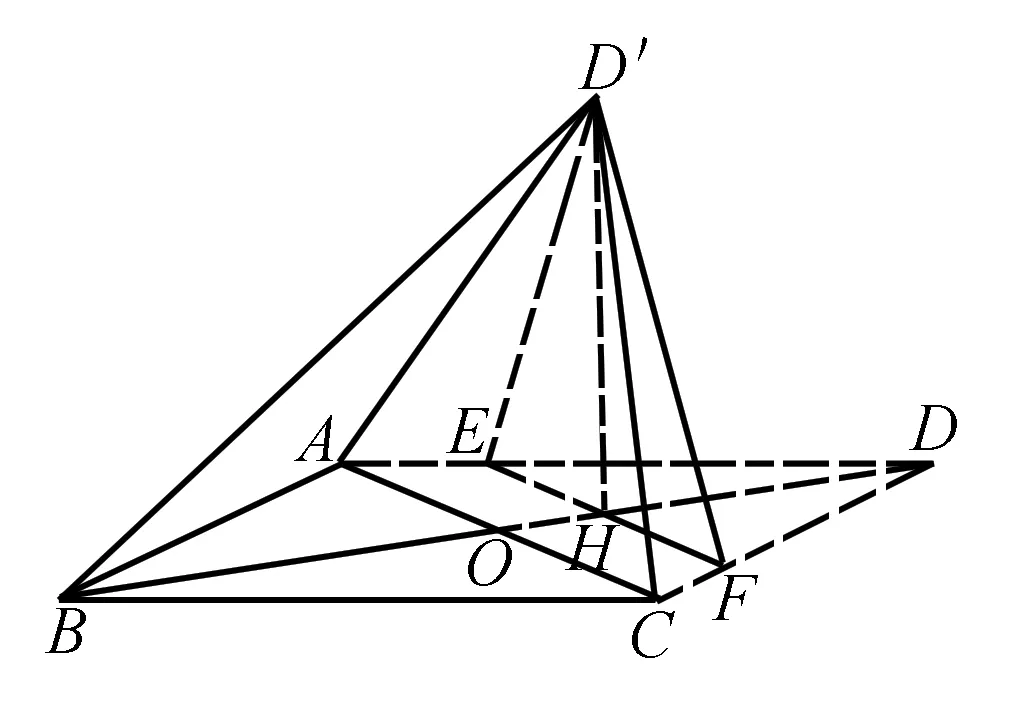
例2 (2016·全国Ⅱ文·19)如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=CF,EF交BD于点H,将△DEF沿EF折到△D′EF的位置.
(1)证明:AC⊥HD′;
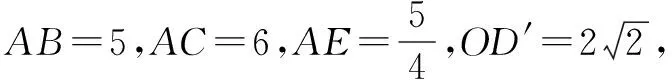
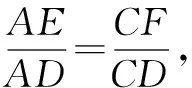
由此得EF⊥HD,EF⊥HD′,所以AC⊥HD′.
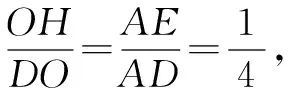
点评在解决翻折中的数量计算问题,一定要准确判定翻折前后哪些数量发生变化、哪些数量没有发生变换,以及翻折后给出的数量关系,结合空间线面的位置关系来处理有关空间角、空间距离以及几何体的表面积或体积等计算问题.
三、翻折中的几何量的最值问题
通过平面图形的翻折变成空间图形,随着翻折的变化,相应空间几何体中的长度、角度等相关的几何量也随之变化,为相应几何量的最值问题的埋下伏笔,也是翻折中难度最高的不定问题.
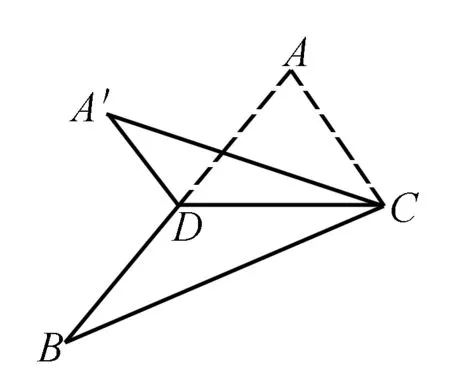
例3 (2015·浙江理·8)如图,已知△ABC,D是AB的中点,沿直线CD将△ACD折成△A′CD,所成二面角A′—CD—B的平面角为α,则( ).
A.∠A′DB≤αB.∠A′DB≥α
C.∠A′CB≤αD.∠A′CB≥α
解析取极限思维:当沿直线CD翻折→180°,此时α→0°,排除A、C;当沿直线CD翻折→0°,此时α→180°,排除D.故选B.
点评在平面图形的翻折变化过程中,一些相关量的变化,如空间几何体中长度、角度等存在最值问题,如何从动态过程中找到此时最值是解决问题的关键,通过翻折使得动态问题静态化,达到求解翻折中的最值问题.
立体几何的翻折问题背景简单,立意深远,对考生空间想象能力要求很高,可以有效改善学生对立体几何的思维定势,构造空间立体几何结构直观图,使静态数学动态化,优化学生的思维品质.
