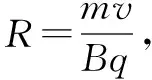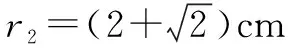大量粒子运动的临界问题

陶汉斌

(浙江金华第一中学 321015)

浙江省的选考物理试题中常出现“大量粒子”的运动问题，由于这类问题涉及的研究对象是大量的粒子，而我们不可能对大量粒子中的每一个粒子都进行分析，那么我们应该如何选取恰当的粒子做为研究对象呢？从粒子源射出的大量粒子有自己的个性与共性问题，比如大量粒子的速率相同而方向不同，比如大量粒子的速度方向相同而速率大小不同.同学们要根据运动的临界条件，恰当地选取“临界”粒子，利用“临界”粒子进行分析使问题变得简洁明了、形象生动.

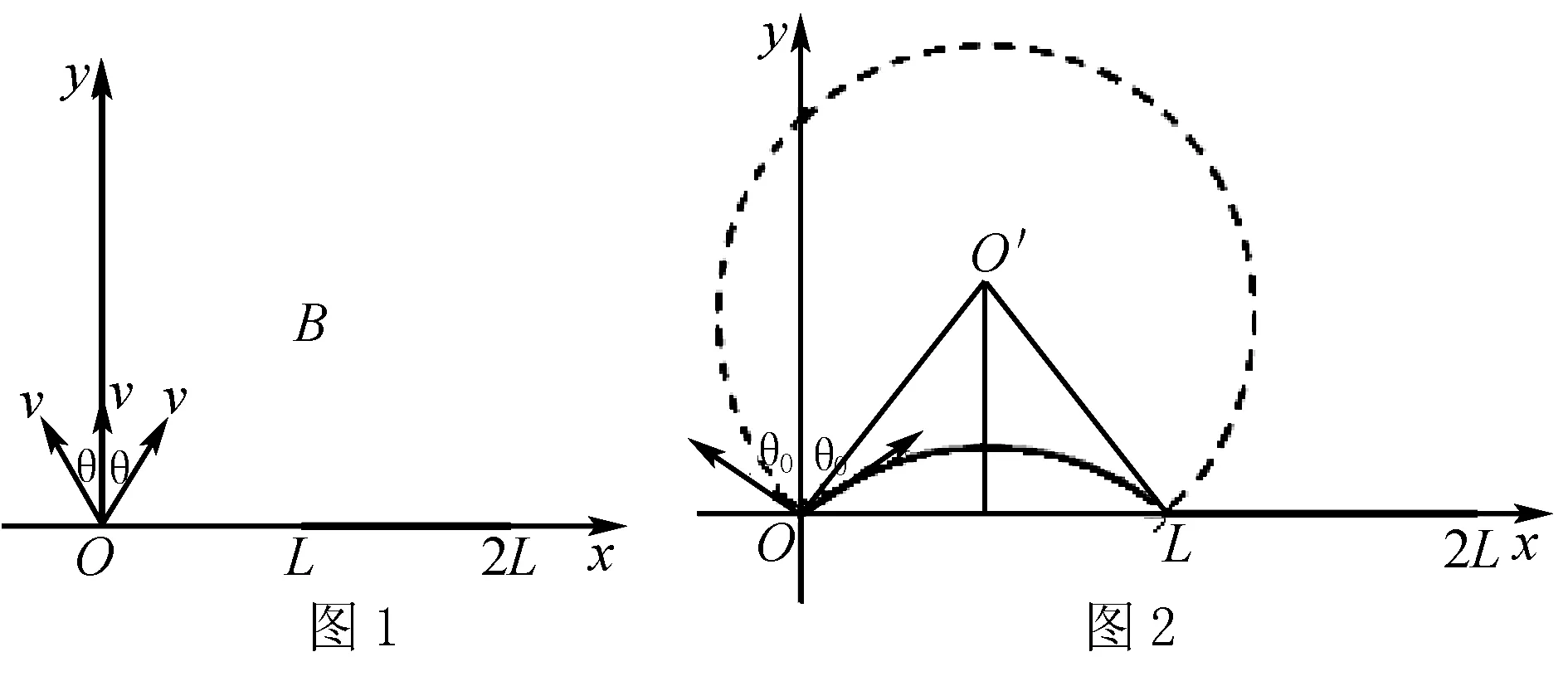
例1如图1所示，x轴上方存在垂直纸面向外的匀强磁场，坐标原点处有一正离子源，单位时间在xOy平面内发射n0个速率均为v的离子，分布在y轴两侧各为θ的范围内.在x轴上放置长度为L的离子收集板，其右端点距坐标原点的距离为2L，当磁感应强度为B0时，沿y轴正方向入射的离子，恰好打在收集板的右端点.整个装置处于真空中，不计重力，不考虑离子间的碰撞，忽略离子间相互作用.

(2)如果发射的离子被收集板全部收集，求θ的最大值；

(3)假设离子到达x轴时沿x轴均匀分布.当θ=37°，磁感应强度在B0≤B≤3B0的区间取不同值时，求单位时间内收集板收集到的离子数n与磁感应强度B之间的关系.(不计离子在磁场中运动的时间)

解析正离子源射出的离子速率是相同的，因此它们在磁场中都做相同半径的匀速圆周运动，只是转过的圆心角不同，也就是经历的圆弧长度不同.那么分布在y轴两侧各为θ的范围内大量粒子，哪个是临界粒子呢？我们知道圆周中最长的弦长是直径，因此沿y轴正方向射入的粒子是打到收集板上最远的临界粒子，而沿y轴两侧以θ角射入的两个离子也是临界粒子，因为这两个离子的弦长是最短的，是打到收集板上最近的临界粒子，其中一个是优弧，另一个是劣弧.具体解答如下：

(1)对带电粒子的圆周运动

而沿y轴正方向入射粒子轨迹为半圆R=L

(2)选取与y轴正方向夹角相同的向左和向右2个粒子为临界粒子.当粒子恰好达到收集板最左端时，θ达到最大，粒子轨迹如图2所示

由图中几何关系得2Rcosθm=L=R

因此可得θmax=600

(3)以沿y轴正方向入射的粒子为临界粒子，打在x轴上距离原点最远的距离为2R.

沿与y轴正方向马θ=37°入射的临界粒子，打在x轴上距离原点最近距离为2Rcosθ=1.6R

也就是说粒子打在x轴上的区间为1.6R～2R，而在x轴上吸收板的区间为L～2L，如图3所示.若全部收集到离子时的最小半径为R1，则有

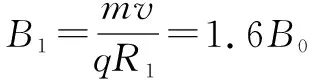
当B0≤B≤1.6B0时收集板上收集到的离子数n1=n0

若恰好收集不到离子时的半径为R2，则有2R2=L

当2B0

例2 如图4所示，在B=0.1 T的匀强磁场中画出 边长为L=8 cm的正方形EFGH，内有一点p，它与EF和FG的距离均为1 cm，在P点有一个发射正离子的装置，能够连续不断地向纸面内的各个方向发射出速率不同的正离子，离子的质量为1.0×10-14kg，电荷量为1.0×10-5C，离子的重力不计，不考虑离子之间的相互作用.(计算结果可保留根号)

(1)速率在什么范围内的离子不可能射出正方形区域?

(2)速率为1×106m/s的离子在纸面上向各个方向均匀发射，求不会射出正方形区域的离子与能射出正方形区域的离子的个数之比.

(3)速率大于多少的离子将全部射出正方形区域？

解析这些大量粒子的速率不同，在磁场中运动的轨道半径也不同，但这些粒子是从同一个点P出发的.在粒子做圆周运动的过程中，弦长最长的是直径.具体解法如下：

(1)P到正方形边界最近的距离为1 cm，选取直径为1 cm向左或向上的粒子为临界粒子，临界条件是粒子运动的轨迹刚好与边界相切.

解得v=5×105m/s

因此只要v<5×105m/s离子不可能射出正方形区域.

(2)速率为v1=1×106m/s的离子在磁场运动的轨道半径为r1=1.0 cm

选取向下和向右运动的粒子为临界粒子，此粒子的临界条件是运动轨迹恰好与边界相切，如图5所示.两个临界粒子速度间角度为900，在360°的整个空间平面内，粒子速度从水平向右顺时针转到竖直向下的90°范围内的粒子将不会射出磁场区域，而再从竖直向下顺时针转270°范围内的粒子将射出磁场区域，因此，不会射出正方形区域的离子与能射出正方形区域的离子的个数之比为1比3.

上文中的两个案例对大量粒子的运动问题进行了分析阐述，求解大量粒子的运动问题时，根据临界条件恰当地选取临界粒子，搞清楚什么物理事件，物理事件的临界条件是什么.

一旦找到了满足临界条件的临界粒子，就可以利用“临界”粒子进行分析使问题变得简洁明了、形象生动.