巧解选择题的几种方法
2018-11-08黄玉梅
黄玉梅
(四川省绵阳师范学院数理学院 621000)
选择题作为客观题的一个大类,在各类考试中被广泛使用,高考物理试题中也不例外.它具有自己独有的特点,即正确答案已经给出在选项中,只需要学生准确将之甄别出来.选择题因其小题较多,考查的物理知识点的范围就比较广,且有些难度并不亚于一般解答题.在做选择题时,如果在某一小题上花费太多的时间和精力是不可取的,因此能否快速摒除干扰信息找到正确选项就显得尤为重要.在下文中,以一些看似比较复杂的题目为例谈几个选择题的解题技巧.
一、整体法
在对两个或两个以上的物体进行研究时,如果物体间具有相互联系、相互作用,则可以考虑将这些物体作为一个整体的系统来讨论,这就是整体法.整体法可以有效减少研究过程中的一些中间物理量,简化解题过程.特别在解决平衡问题时,遇到可以无需考虑物理间的相互作用的情况,则采用整体法尤为便利.

图1
例如图1所示,两个带有同种电荷的小球,用绝缘细线悬挂于O点,若q1>q2,l1>l2,平衡时两球到过O点的竖直线的距离相等,则( ).
A.m1>m2B.m1=m2
C.m1 答案:选B. 分析可将两个小球视为一个整体,所受电场力是一对作用力与反作用力,大小相等,方向相反,在同一条直线上,在体系中可以处理为内力,q1>q2并不影响这一结论.因此,体系所受的外力只有拉力和重力. 因体系只受拉力和重力,可考虑采用找体系重心的方法,该体系的重心(其实是质心,但在尺度不大的情况下,可认为两心重合)应该在m1和m2连线上;当体系被悬挂于O点时,重心在平衡时应该在过O点的竖直线上,因此m1和m2连线与过O点的竖直线的交点就是重心.如图1,由几何关系可知,该交点位置恰平分m1和m2连线,即重心在m1和m2连线的中点处,则要求m1=m2. 该方法应用了体系的重心这一概念,是整体法的典型应用,避开了共点力的平衡的讨论,解题速度大大提高.但是对学生而言,可能对把两个小球作为一个整体来考虑不太熟悉,因为在力学问题的分析中,日常练习的时候“隔离法”更为常见,“整体法”用得反而不多.但是对于上述题目,如果对每个小球做受力分析,求解过程会比较繁琐,要得到结果很费时费力,并不可取. 面对一个较为复杂的物理现象、物理过程或者物理问题时,用比较简单的物理模型或者假设来进行替代,使得最后达到的效果相同,这就是等效法.该方法在解答选择题时,能有效地化繁为简,达到快速解题的目的. 图2 例一架飞机在高空中沿水平方向做匀加速直线飞行,每隔相同时间空投一个物体,不计空气阻力.地面观察者画出了某时刻空投物体的4幅情景图(如图2),其中可能正确的是:答案:选C. 分析以地面为参考系,从飞机上释放物体,不考虑空气阻力,物体做平抛运动,因为飞机做匀加速直线运动,所以每次空投物体时,物体所获的平抛初速度越来越大,在讨论扔下后的空间分布时,计算是比较麻烦的,如果采用等效法则不然.如图2可以看出,几个物体的空间位置是以飞机为参照物的,则可以建立一个与飞机相对静止的参考系,此参考系具有水平向右的加速度a,是非惯性系,要保持牛顿定律在该参考系中成立,需要引入一个惯性力,惯性力对物体产生的加速度大小为a,方向水平向左. 排除法指的是根据题目中给出的物理信息,结合相关的物理知识直接分析选项,将与题意明显不符或者与已知条件无关的选项进行排除的解题方法. 假设法则是在处理物理问题时,对物理模型、物理过程或者物理量的结果进行适当地假设,避开比较复杂的讨论,以进行下一步的研究. 在处理选择题时,假设法常和排除法结合,可以提高甄选正确选项的效率. 例(多选题)如图3所示,轰炸机沿水平方向匀速飞行,到达山坡底端正上方时释放一颗炸弹,并垂直击中山坡上的目标A.已知A点高度为h,山坡倾角为θ,由此可以算出( ). 图3 A.轰炸机的飞行速度 B.炸弹的飞行时间 C.轰炸机的飞行高度 D.炸弹投出时的动能 答案:选ABC. 分析此题可以根据“垂直击中山坡上的目标A”这一关键条件得到在A点时飞机的水平速度和竖直速度的关系,从而根据平抛运动的公式来进行推导,找到正确选项.但是这一方法涉及速度的分解、运动公式的应用等知识点,比较繁琐,而且稍不注意就会漏掉选项. 当遇到的物理问题涉及的变化较多或过程复杂时,可以对几个比较容易处理的特殊状态进行分析,这就是特殊状态法,是一种把一般问题化简为特殊状态的方式,有时可以起到破冰的效果. 图4 A.MN上的张力逐渐增大 B.MN上的张力先增大后减小 C.OM上的张力逐渐增大 D.OM上的张力先增大后减小 答案:选AD 分析本题考查共点力的动态平衡,重物受重力和两个夹角恒定的拉力,而拉力的大小、方向在整个物理过程中都是变化的,难度较大.对于此题用几何法比较明晰,即平衡时三力合力为零,利用合力的三角形法则可以构成封闭的三角形,再借助几何中圆的相关知识就可以得到结论.但是这种方法抽象性很强,且对几何构图的能力要求很高,一般同学很难在考试的紧张气氛中马上想到这一方法.可采用特殊状态法,可能严密性不足,但比较直观. 图5 如图5,选择OM竖直、MN水平和OM水平这三个特殊状态,分析每个状态的情况,对每个状态的MN和OM的张力在水平方向和竖直方向上进行分解. 对OM竖直状态平衡时有:TOM1=mg,TMN1=0 对OM水平状态平衡时有: 此时已经可以进行几个状态的张力比较了,但为了完整起见,可以想象如果N点继续上移到MN竖直状态,那么就会有TOM4=0,TMN4=mg.由此,容易根据三角函数关系得到TOM2>TOM1和TOM2>TOM3>TOM4,TMN3>TMN2>TMN1和TMN3>TMN4,而且还可以看出,MN水平状态和OM水平状态的MN和OM的张力具有对称性;MN竖直状态和OM竖直状态的MN和OM的张力也具有对称性.由对称性可得,从OM竖直到OM水平状态,OM上的张力是先增大后减小,MN上的张力逐渐增大.如果是从MN竖直状态到MN水平状态,则是MN上的张力是先增大后减小,OM上的张力逐渐增大.而MN水平状态是OM上的张力最大的时候;OM水平状态是MN上的张力最大的时候. 这一方法似乎远不如合力的三角形法则结合圆的几何知识来得简单,但是在学生一时想不到几何法的时候不失为一种值得尝试的方法,比之完全无法下手来说至少有了一个解题方向. 该缺点的方法是不够严密,因为选取的特殊状态是特殊情况,推广到一般情形的时候会不会有更复杂的情况发生很难预计;且张力最大的状态的证明也不严密,如果是填空题或问答题就不适用了,只有在做选择题的时候可以考虑使用.二、等效法

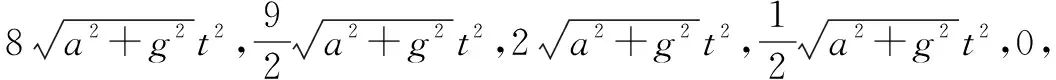
三、排除法和假设法相结合


四、特殊状态法