用夹逼法解决求值问题

郭洪林

(黑龙江省哈尔滨市第三中学 150001)

求字母或式子的值是数学中常见问题.这类问题由于题目类型多，求解方法也是各种各样.但有一种方法——夹逼法是别具特色的.为了求x的值，一方面我们可以推得x≥a，另一方面我们又可以推得x≤a，从而夹逼出x=a.

下面我们分类举例来体会夹逼法的几种实施方式.

一、利用不等式

分析显然由题设的两个关于a、b、c的方程无法解出三个未知数a、b、c的值.可把式子abc作为一个整体来求解.不难观察到，利用基本不等式可以构建起abc与已知式的联系.

解根据基本不等式，一方面有

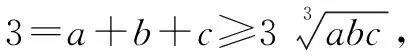
由①和②可得abc=1.

二、巧用平方数非负

例2 求满足条件2x-4y+6z>x2+y2+z2+13的整数x、y、z的值.

解将不等式移项，配方可得(x-1)2+(y+2)2+(z-3)2<1.

而(x-1)2、(y+2)2、(z-3)2均非负，故有

0≤(x-1)2+(y+2)2+(z-3)2<1.

但(x-1)2、(y+2)2、(z-3)2都是非负整数，所以只能有x-1=0,y+2=0,z-3=0,从而得x=1,y=-2,z=3.

点评本解法通过配方，利用非负数夹出式子的较小的范围，再用整数的条件，逼出具体值.

三、多次用判别式

x2+ax+b+1≥0，故Δ1=a2-4(b+1)≤0 ①.

由①和②知有

Δ1=a2-4(b+1)=0 ③.

联立③和④，可解得a=±4,b=3.

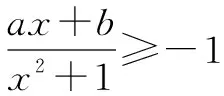
四、不断构造函数求最值

例4 (2017年全国Ⅱ卷21(1)题)已知函数f(x)=ax2-ax-xlnx,且f(x)≥0，求a的值.

解法1 (多次分类讨论)由题设知f(x)的定义域是(0,+∞)，因此f(x)≥0等价于恒有g(x)=ax-a-lnx≥0(*).

(1)当a≤0时，易见g(2)=a-ln2<0,(*)式不成立，故必有a>0.

(2)当a>0时，(*)式恒成立，即g(x)的最小值≥0.以下来求g(x)的最小值.

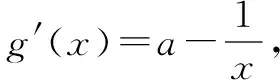
她为沐浴后的秦川按摩，她让秦川变得赤裸。她仔细检查秦川的耳垂，腋窝，膝窝，脚踝，脚跟，脚趾……她没有发现一道哪怕最微小的伤痕。她让秦川翻过身来，她的指尖和目光将秦川的每一处探遍。

故有h(a)=1-a+lna≥0 ①.

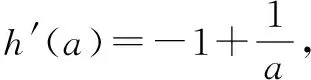
当a∈(0,1)时，h′(a)>0，h(a)递增；当a∈(1,+∞)时，h′(a)<0,h(a)递减，所以h(a)的最大值是(h(1),)即h(a)≤h(1)=0，得

1-a+lna≤0 ②.

由①和②得1-a+lna=0 ③.

为了解出a，现构造相应函数k(x)=1-x+lnx，来求k(x)的零点.

易见k(1)=0.利用导数易知k(x)在(0，1)上递增，在(1，+∞)上递减，故k(x)的最大值是k(1)=0.这样，k(x)有唯一的零点x=1.

所以方程③有唯一解是a=1.

点评1.本解答中，一方面由g(x)min≥0推得h(a)=1-a+lna≥0,另一方面又求得h(a)的最大值是h(1)=0,推得h(a)=1-a+lna≤0，从而夹逼出h(a)=1-a+lna=0.

2.本解答中，不断地构造相应的函数，利用导数求出最值，零点，充分体现了函数、导数的工具作用，这是高考考查的重点和难点.

解法2 (分离参数)

由解法1有ax-a-lnx≥0，即a(x-1)≥lnx在x∈(1,+∞)上恒成立.

(1)当x=1时，显然a(x-1)≥lnx恒成立.

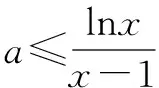
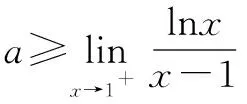
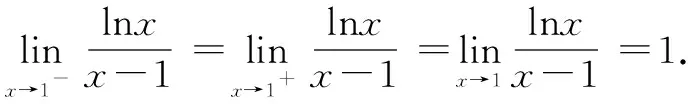
结合①和②可知a=1.

下面给出一道题，供练笔.

设函数f(x)=ax3-3x+1，若对于任意x∈[-1,1]都有f(x)≥0成立，求实数a的值.(答案：a=4)