三并联万向节数控磨床的球铣刀后刀面建模
2018-11-08赵林
赵 林
(河南中烟工业有限责任公司安阳卷烟厂,河南安阳 455000)
0 引言
刀具的大量使用使得刀具刃磨越来越受到重视,尤其是复杂结构刀具的重新刃磨对于企业提高生产效率,降低生产成本显得至关重要,球铣刀作为一种复杂结构刀具,其刃磨困难,刃磨成本高。国内外生产厂家与高校科研机构均研发出不同类型的刀具刃磨机床,但是这些机床几乎都是串联结构,并联结构形式的刀具刃磨机床鲜有实际应用。基于东北大学自主设计制造的三并联万向节数控刃磨机床[1],进行螺旋刃球铣刀后刀面建模研究,为后续编程刃磨实验做好理论基础。
1 三并联万向节数控磨床简介
三并联万向工作头数控磨床(图1)由5个伺服电机驱动。并联杆电机控制2个并联支链分别实现等量伸缩进而使工作头绕X轴的摆动,也可以控制2个并联支链同步等量伸缩实现工作头绕Z轴的摆动,若并联支链的伸缩不等量则可以实现工作头绕xOz平面内任意方向摆动。横向滑移电机和纵向滑移电机可以使工作头实现横向与纵向进给。主轴电机可控制工件绕摆动以后的主轴方向转动。当工作头摆动一定角度之后,纵向进给方向并不是沿工作头末端执行器的轴线,而是保持原来方向不变。
2 球头立铣刀刃口曲线的数学模型
根据现有三并联万向节数控机床的运动特点及结构特点,在参考已有的球头铣刀数学模型[2-6]的基础上重新建立螺旋刃球铣刀球头部分刃口曲线的数学模型,如图2所示。

图1 三并联万向节数控磨床
O点为万向节的摆动中心,O—XYZ为铣刀结构坐标系。O1—X1Y1Z1为铣刀的球面坐标系,O1为铣刀球头中心,R为球面半径。P为球面上任意一磨削点,P1为点P在球面底面圆环上的投影,θ为刃口曲线上磨削点P与X1Y1平面的夹角,φ为P1与X1轴的夹角,H为2个坐标原点间的距离,λ为点P1与Z轴的夹角,l为OP的长度。
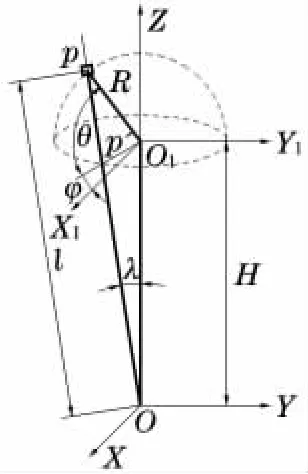
图2 球头铣刀刃口曲线数学模型
基于三并联万向节数控机床的球面螺旋线磨削可看作这样一种运动:点P在坐标系O1—X1Y1Z1中的摆动和绕Z1轴的转动相互作用形成球面螺旋线,杆长O1P保证了球面半径为R。形成球铣刀刃口曲线的过程中,并联机床的两根并联杆做完全相反的匀速伸缩运动,使得杆OP绕摆动中心匀速摆动,摆角为λ,同时纵向滑台进给η,根据相对运动,可看作滑块沿杆OP滑动,杆OP长度缩短η,即λ角和长度l时刻在变化。在坐标系O1—X1Y1Z1中球面刃口曲线可表示为:x1=Rcosθcosφ,y1=-Rcosθsinφ,z1=Rsinθ,其中,θ与 φ 存在一定的函数关系。
在坐标系O—XYZ中铣刀球面刃口曲线可表示为:x=lsinλcosφ,y=-lsinλsinφ,z=lcosλ,其中,φ,l均与 λ 存在一定的函数关系。在坐标系O—XYZ中正交螺旋面可表示为:x=Rzcosφ,y=-Rzsinφ,z=Pzφ/2π+H。在三角形 OPO1中,由余弦定理可知,cosλ=(l2+H2-R2)/2lH,即 l2-2lHcosλ+H2-R2=0。解得:l=Hcosλ±当λ=0时l=R+H,因此可将负号解排除,所以l=又因为 η=R+H-l,故 η=R+H-Hcosλ+联立 x=lsinλcosφ,y=-lsinλsinφ,z=lcosλ 和 x=Rzcosφ,y=-Rzsinφ,z=Pzφ/2π+H 可得:Pzφ/2π+H=lcosλ。解得,φ=(lcosλ-H)tanβ/R,其中,β为铣刀螺旋角(与轴线夹角),tanβ=2πR/Pz,其中,Pz为导程。在坐标系O—XYZ中铣刀球面单侧刃口曲线可表示为(1)式。
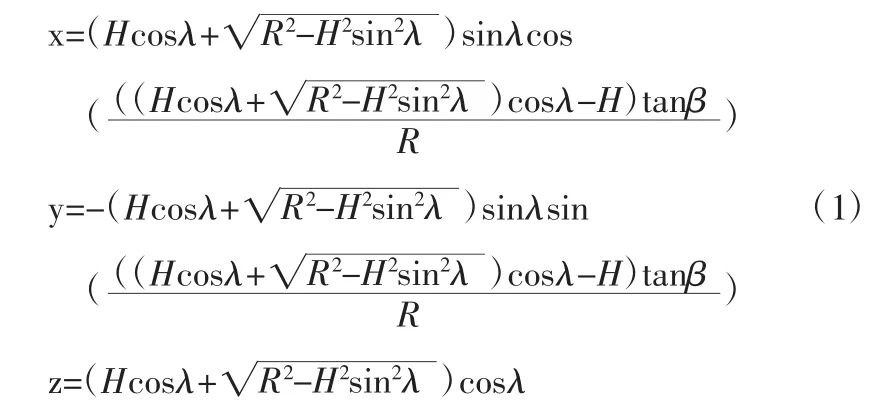
另一侧刃口曲线根据球铣刀的对称性可求出,在此不再列出。设 R=5 mm,H=20 mm,β=30°,刃口曲线如图 3所示,呈现明显的S形,其中左图为刃口曲线主视图,右图为刃口曲线俯视图。

图3 刃口曲线
3 后刀面数学模型
采用圆柱砂轮边缘刃磨球铣刀后刀面,后刀面成形原理如图4所示。其中,O—XYZ为球头立铣刀结构坐标系;O3—X3Y3Z3为坐标系O—XYZ绕Z轴旋转角度φ后形成的坐标系;O4—X4Y4Z4为坐标系 O3—X3Y3Z3绕Y3轴旋转角度λ后形成的坐标系,此时砂轮刚好与球面相切于P点。为能刃磨到P点,此时铣刀坐标系已绕Z轴和Y3轴分别旋转了角度φ和λ。后刀面与砂轮边缘接触线在坐标系O4—X4Y4Z4中可表示为(2)式。

图4 后刀面刃磨示意图

将其转化到坐标系O3—X3Y3Z3中,得到(3)式。

在球铣刀结构坐标系O—XYZ中后刀面可表示为(4)式。

式(2)中,α为铣刀球面刃后角,lα为后刀面直纹线MN上任意磨削点距刃口曲线的距离,0≤lα≤d,d为后刀面宽度。联立(2)、(3)、(4)式可得第一后刀面方程,见(5)式。
球铣刀两部分后刀面关于轴线对称,另半部分后刀面为式(6)。

设 R=5 mm,H=20 mm,β=30°,d=0.5 mm,α=15°,所得后刀面如图5所示。
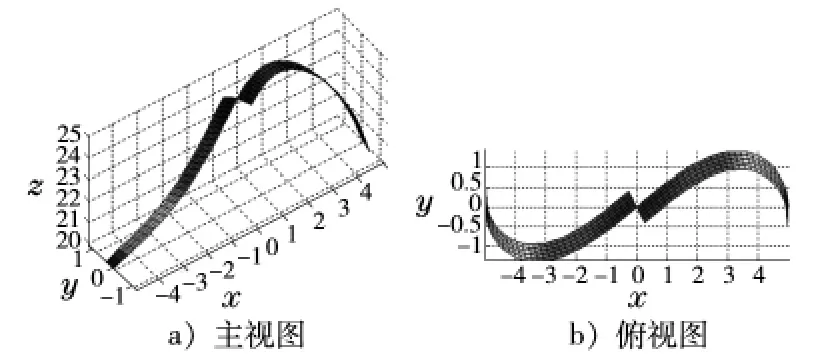
图5 球铣刀第一后刀面
通过球铣刀第一后刀面的仿真图可以看出,图形与球铣刀第一后刀面的实际形状吻合,说明所建立的第一后刀面数学模型正确。
4 结论
在参考球头铣刀数学模型的基础上,建立了适合三并联万向节数控磨床运动特性的球铣刀刃口曲线和第一后刀面数学模型,并通过matlab仿真验证了数学模型的正确性,为后续刃磨程序的编写做好基础。
