基于最小二乘支持向量机的矿用胶带机滚动轴承故障识别
2018-11-08徐其祥
徐其祥
(河南省平顶山市平煤集团公司 六矿,河南 平顶山 467000)
矿用胶带机作为一种运输煤炭的工具,广泛应用于煤炭开采工业中,滚动轴承是胶带机的重要零部件,其运行状态直接影响到设备的整体性能,开展其故障识别研究具有重要意义[1-2]。定期检查和事后诊断是目前现场常用的2种诊断方式。定期检查需要胶带机停机,这样会严重影响煤炭生产效率,降低企业效益,另外当故障突然发生时,定期检查也很难发现。事后诊断则发生在胶带机轴承出现故障后,故障的发生危及企业的安全生产,给企业和员工带来严重的损失。为此国内相关专家学者针对胶带机滚动轴承快速诊断开展了大量的研究,取得了一系列成果。杨宇[3]针对滚动轴承故障振动信号的非平稳特征,采用经验模态分解法将非平稳振动信号进行了分解,提取各IMF分量中的特征参数作为神经网络的输入参数来开展滚动轴承的故障类型识别;周川[4]提出了一种基于经验模态分解和奇异值分解的特征提取与模糊C均值(FCM)聚类的滚动轴承故障诊断方法,对滚动轴承故障进行分类;张玲玲[5]基于集合经验模态分解法和模糊C均值聚类分解提取发动机曲轴故障特征,最后识别出轴承的磨损程度;胡爱军[6]证明了包络解调方法能够准确提取滚动轴承故障特征信息,认为它能够实现滚动轴承故障的精确诊断;康守强[7]采用改进分类规则的超球多类支持向量机进行滚动轴承分类时,提出由各状态超球球心间距中的最值来确定多类分类器核参数的选取范围,缩小了选取区间;郭谋发[8]计算了变换构造配电开关振动信号的时频矩阵的奇异值,并将它作为特征向量对配电开关典型故障进行分类;张淑清[9]对机械振动信号进行LMD分解,得到若干具有物理意义的乘积函数(product function,PF)分量,再通过相关性分析得到与原始信号相关性最大的分量,求取其近似熵作为特征向量开展故障识别分类。
胶带机轴承在出现故障时,振动信号常常会呈现出非平稳的特征,包含一些突变点。本文采用最小二乘支持向量机方法,利用小波包的分解方法提取检测信号的故障信息,并将其作为最小二乘支持向量机的输入量,将样本的常见故障类型作为输出量,开展了胶带机滚动轴承故障的识别研究,对胶带机滚动轴承快速准确地进行故障诊断具有重要的理论和现实意义。
1 最小二乘支持向量机
支持向量机作为一种新型学习机器,是在统计学习理论上发展得到的,最小二乘支持向量机[10]在充分利用已有优先信息的基础上,最大程度地降低复杂度,将标准支持向量机算法中的不等式约束利用等式约束替换,同时用直接求解线性方程组代替原有的求解二次规划问题,保证了模型具有较强的实用性。在解决小样本、非线性、高维数和局部极小点等问题方面具有绝对优势,广泛应用于类别识别、效果评价和参数预测等方面研究。
设样本集S={(xi,yi)}(i=1,2,…,N),其中N为样本总数,xi和yi分别为输入量和输出量。引入松弛向量εi来描述分类超平面,设置约束条件:
yi[ωTφ(xi)+b]-1+εi=0
(1)
式中,φ(xi)为输入量在高维空间的映射;ω为超平面的法线方向;b为常数。
最小二乘支持向量机方法要求训练集到超平面的最小距离最大,因此确定最优超分类面的问题转换为二次规划问题:
(2)
式中,c为惩罚因子。
建立拉格朗日函数来解决上述问题:
(3)
式中,α为拉格朗日因子。根据优化条件得到:
(4)
求解得到最小二乘支持向量机模型为:
(5)
式中,κi(x,xi)为核函数。径向基核函数是常用的核函数,分类效果较好,其表达式为:
κi(x,xi)=exp(-‖x-xj‖2/σ2)
(6)
式中,σ为核宽度。
通过不断的训练,得到最小二乘支持向量机模型后,就可以开展类别识别、效果评价和参数预测等方面研究。
2 基于最小二乘支持向量机滚动轴承故障识别模型的建立
应用最小二乘支持向量机模型进行矿用胶带机滚动轴承故障识别的基本思路:把样本出现故障时的振动信号作为输入量,将样本的故障类型数据作为输出量,对样本的输入和输出量进行不断的训练学习,得到最小二乘支持向量机模型,利用该模型进行矿用胶带机滚动轴承故障识别,包括4个步骤:收集矿用胶带机滚动轴承故障的振动信号数据;根据搜集得到振动信号提取出特征向量;建立基于最小二乘支持向量机的故障诊断模型;判断矿用胶带机滚动轴承故障类型,输出故障诊断结果。
在构建最小二乘支持向量机矿用胶带机滚动轴承故障诊断模型时,首先要根据振动信号提取特征向量,本文采用小波包分析方法[11],它具有较强的信号分析能力。频带分解过程如图1所示,在此过程中,小波包将上层的n个频带分解成下层的2n个低频带和2n+1个高频带。小波包将离散的信号分解成2n个频段后,统计频带内的能量,将结果做为最小二乘支持向量机输入的特征向量。对于频带Sji(Sji表示j层的第i个频带),其频带能量计算公式如下:
(7)
为了方便分析,对特征向量进行归一化。
T′=[Ej0/E,Ej1/E,…,Ej(2i-1)/E]
(8)
(9)
式中,T′为归一化特征向量;Eji表示j层的第i个频带的能量;E为第j层所有频带能量的算术平方根。
诊断效果与j的取值密切相关,如果j取值过小,提取出的振动信号信息就有缺失,如果j取值过大,运算速度就会变慢。本文在进行小波包分析时,将j取值为3。
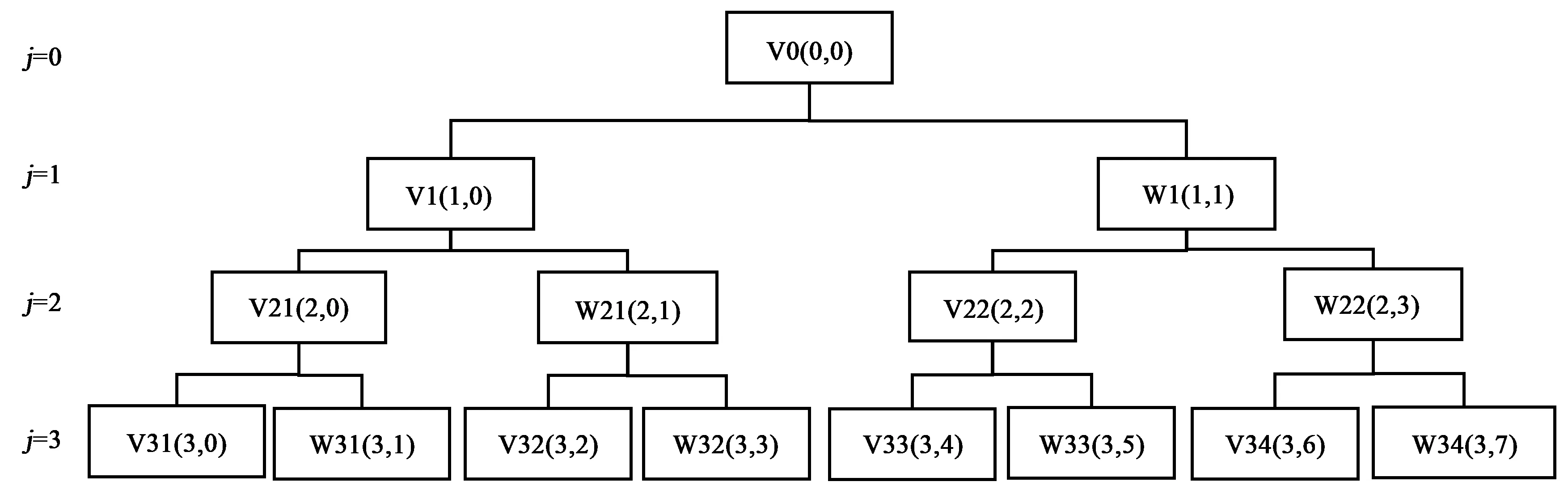
V—低频信号;W—高频信号图1 振动信号小波包分解示意
3 实例分析
滚动轴承实验对象的型号为NJ220EC,实验条件如下:轴承的钻速为290转/min,每组采样点数为1024个。利用小波包信号分析技术将信号分解成3个层8个频带,统计各个频带的能量并进行归一化处理,得到的结果作为最小二乘支持向量机的输入特征向量。滚动轴承主要由4个部件组成,分别为内圈、外圈、滚动体以及保持架。滚动轴承发生故障时外圈、内圈以及滚动体与外圈或内圈接触特征频率计算方法如下:
z个滚动体与外圈上接触频率为:
(10)
z个滚动体与内圈上接触频率为:
(11)
滚动体与外圈或内圈接触频率为:
(12)
式中,fs为内圈旋转频率;fo为外圈故障频率;fi为内圈故障频率;fr为滚动体故障频率;fe为滚动体自转频率;fb为保持架旋转频率;z为滚动体数;d为滚动体直径;D为轴承节径;α为轴承的压力角。根据以上分析将正常运转、内环故障、外环故障和滚动体故障作为4种运行状态,并作为最小二乘支持向量机输出层的4个节点,训练的总样本数为40,每种状态各10个样本,图2显示外环故障的原始信号,利用小波包分解法提取这4种状态下的能量特征向量,表1为部分提取的能量特征向量归一化的结果,其理想输出见表2。
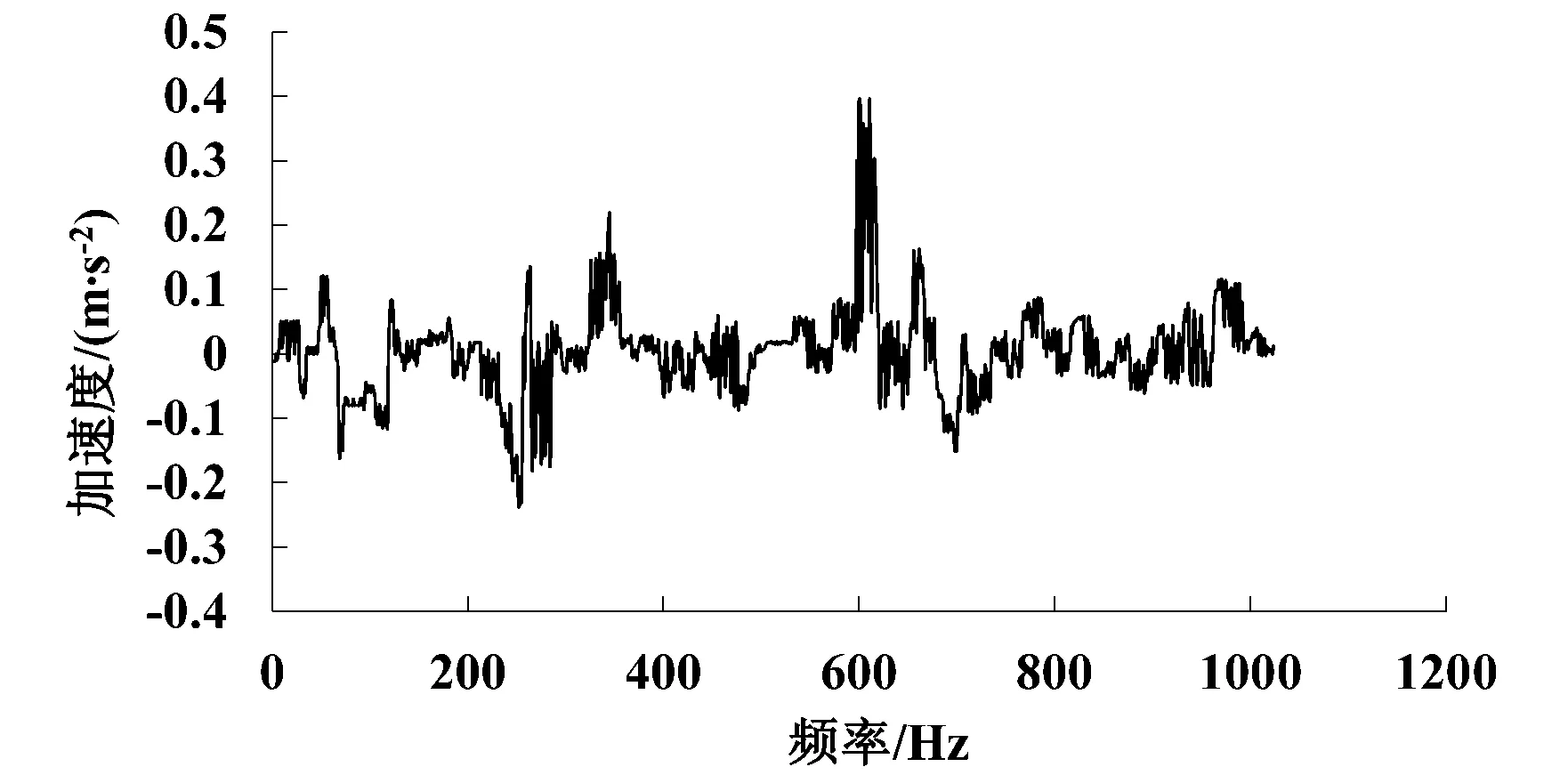
图2 外环故障的原始信号
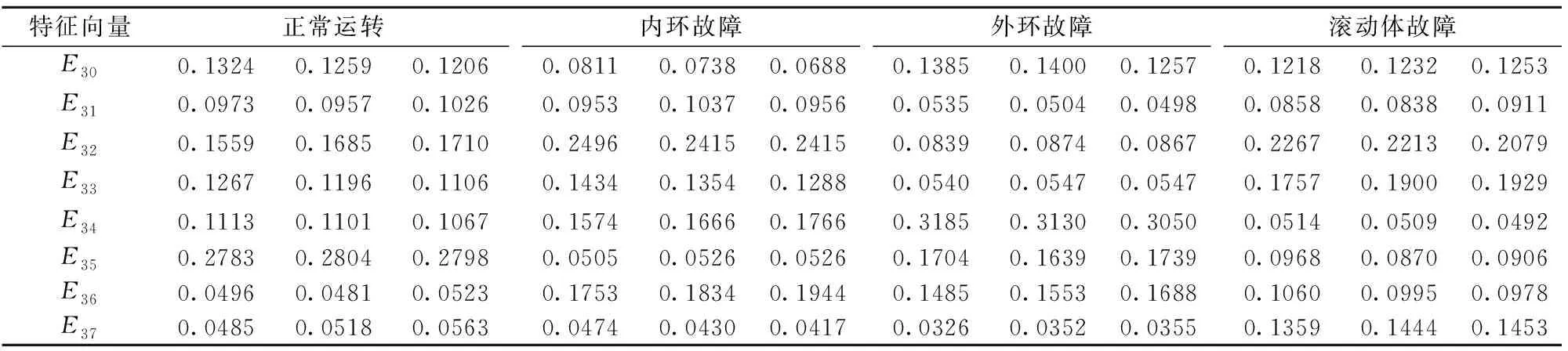
表1 小波包提取的不同状态能量特征向量
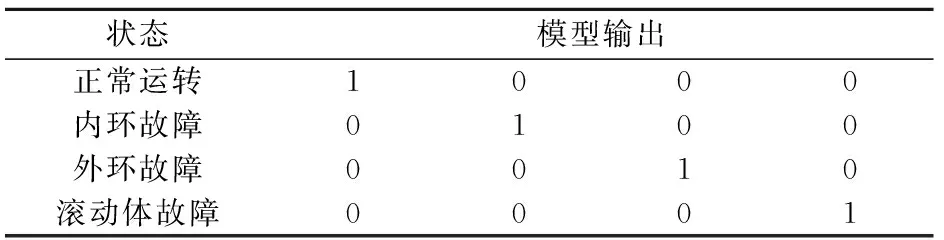
表2 训练样本的输出
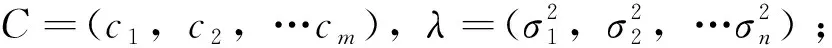
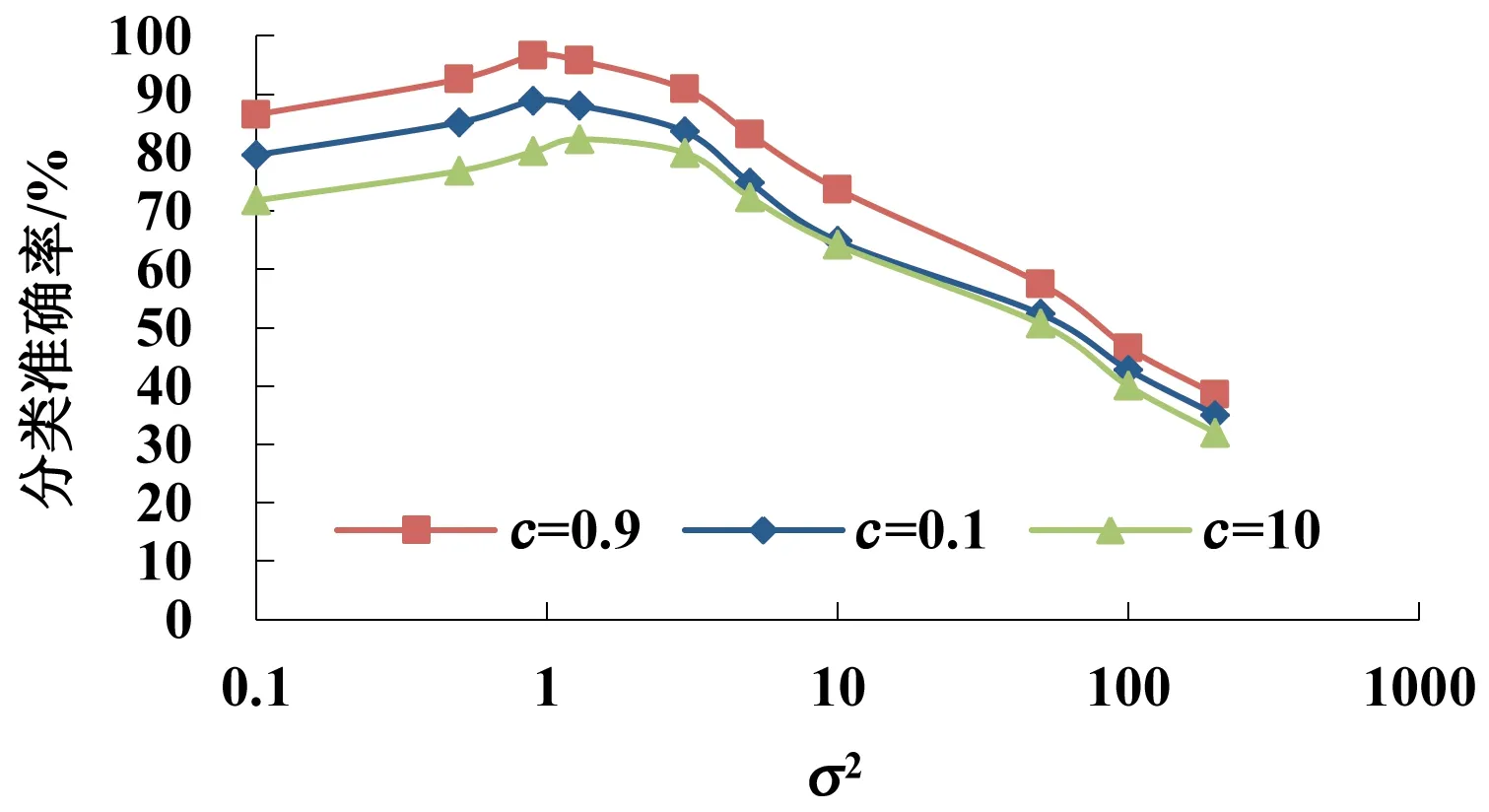
图3 分类准确率变化曲线
为了进一步验证模型的合理性,利用训练好的支持向量机模型,每种状态对应20个测试样本,将80个样本的信号分析结果输入到已训练好的最小二乘支持向量机模型中,为了验证本文方法的有效性,选择BP神经网络进行对比分析。BP神经网络的结构采用8-5-1,最小允许误差为0.0001,选用sigmoid作为激励函数。两种故障识别模型对测试集判定情况如表3所示。
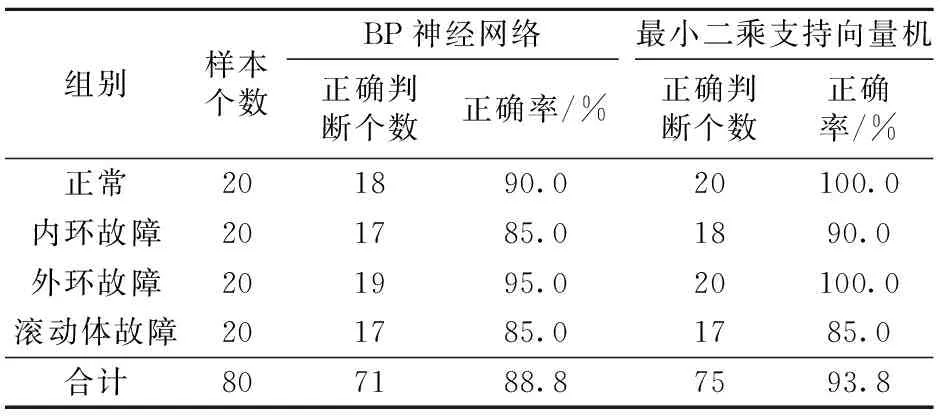
表3 测试样本分类结果比较
由表3可见,80个测试样本中,75个样本可正确诊断,准确率为93.8%,BP神经网络分类的精度为88.8%,相对较差,这是由于小样本,高维数等原因造成的BP神经网络精度较低。综上所述发现,本文的方法可以满足实际工程的需要,进一步验证了模型的有效性以及方法的合理性。
4 结束语
利用最小二乘支持向量机能较好地解决小样本、非线性、高维数和局部极小点,开展矿用胶带机滚动轴承诊断。矿用胶带机滚动轴承的故障分析的实例表明,基于最小二乘支持向量机的方法对故障类型的识别具有一定的实用性,具有广泛的应用前景。
(1)小波包分析能够从复杂的振动信号中提取出包含平稳成分的瞬态信号,具有一定的抗干扰能力和滤波作用,分解后的各个频带内的能量可以作为最小二乘支持向量机模型的输入量。
(2)建立了基于最小二乘支持向量机模型的矿用胶带机滚动轴承的故障识别模型,利用该模型可以对其他机械故障进行诊断和识别,具有较强的推广性。
