基于CSM模型硬岩滚筒载荷理论研究

宋 丹，高立君，王 锴，江 帅

(中铁工程装备集团有限公司，河南 郑州 450016)

硬岩掘进机(Tunnel Boring Machine,缩写TBM)广泛应用于水利水电隧洞、铁路公路交通隧洞、煤矿巷道及城市地铁等地下工程隧道的施工。盘形滚刀与岩石相互作用是TBM的设计和应用方面的关键理论。自1956年发明盘形滚刀以来，国内外许多人对这一理论作了大量的研究工作，其中克罗拉多矿学院(CSM)J.Rostami等人对广泛应用的盘形滚刀破岩进行了研究[1-2]，给出了CSM改进模型，在工程上得到了较多的应用。

根据需要改变尺寸，滚筒刀盘可以方便地开挖平底的矩形断面。与传统的圆形断面隧道相比，矩形隧道有效利用面积高[3]，公路隧道、铁路隧道、地铁隧道、人行地道、地下共同沟的断面形式以矩形最为合适和经济，所以，近几年来矩形断面隧道的应用越来越广泛。国内外对矩形刀盘的受力状况做了大量的理论研究和试验[4-11]，刘春生对装备截齿的滚筒刀盘进行了详细的受力分析[12]；J.Rostami等通过试验验证了装备盘形滚刀的滚筒刀盘破岩的可行性并获得了数据[13-15]。本文将从装备盘形滚刀的滚筒刀盘切削出的轨迹着手，基于CSM改进模型，对滚筒刀盘载荷进行理论分析。

1 CSM改进模型

1993年，Jamal Rostami 等人在对TBM上广泛应用的恒截面(CCS)盘形滚刀进行了研究，在原CSM模型(V形刀刃)的基础上进行了改进，改进后的公式在一定程度上可以预测盘形滚刀受力，并广泛应用于TBM设计上。CSM滚刀模型为现在常用的型式(见图1)。图中R为盘形滚刀半径，T为刀刃宽度，S为相邻滚刀的间距，p为截割深度，φ为接岩角度(rad)，切入点为O点。

则有：

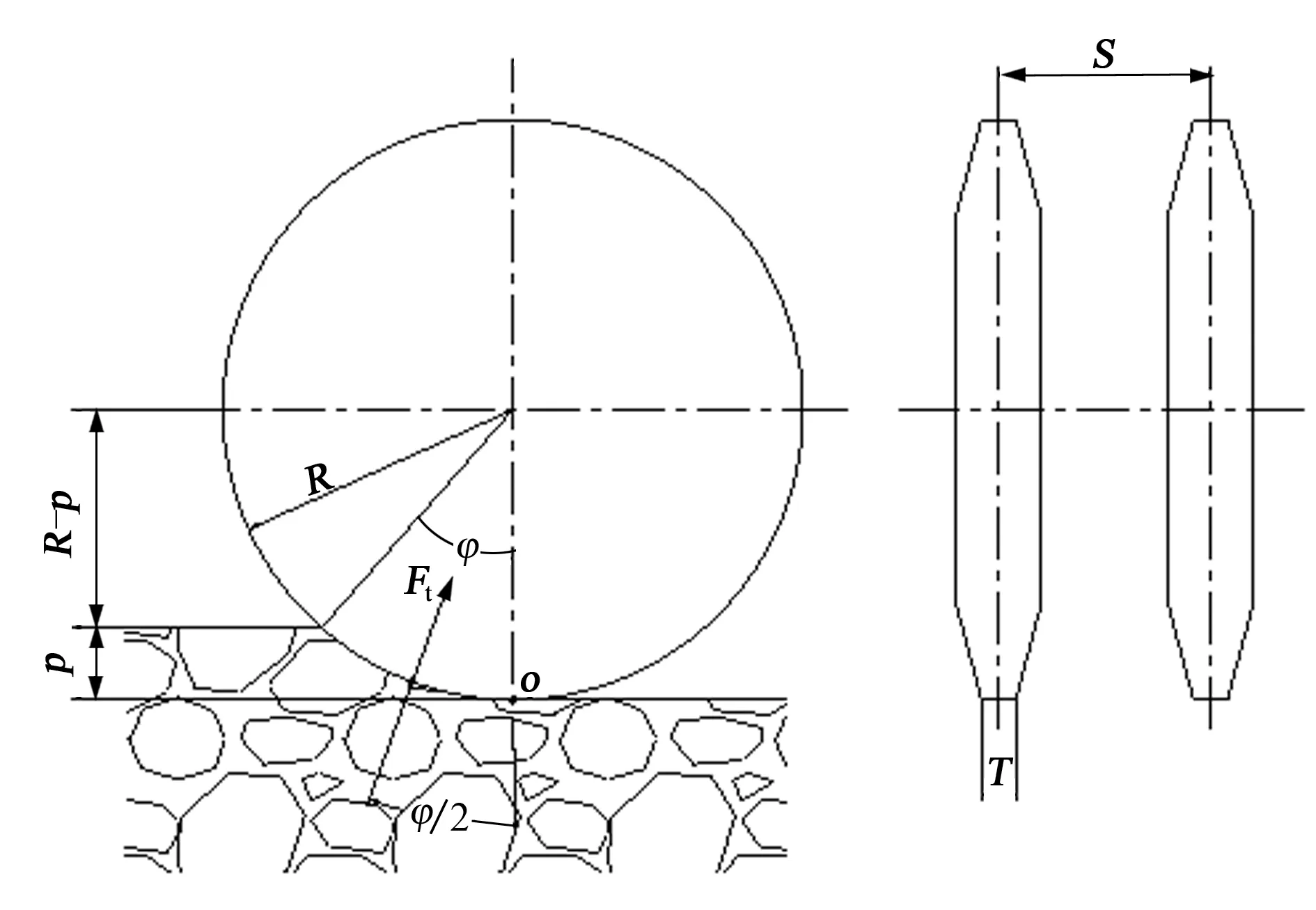
图1 CSM盘形滚刀数学模型

盘形滚刀切削硬岩时，截割深度p,接岩角度为φ，所产生的切削总力Ft为：

式中，P′为破碎区基本应力；R为滚刀刀刃半径；T为盘形滚刀刀刃宽度；ψ为刀刃应力分布系数，取-0.2～0.2,一般取0.1。

式中，C为系数，通常取2.12；σc为岩石单轴抗压强度；σt为岩石抗拉强度；S为相邻刀具间距。

Ft方向如图1，本模型中忽略滚刀中心轴对刀具的摩擦力，该力指向盘形滚刀的中心。

从CSM模型的推导过程可以看出，该模型适用于比较平的切削面，本文将此模型的应用范围进行了拓展，应用于曲率半径较大的圆弧面。

2 装备盘形滚刀的滚筒刀盘切削面几何参数分析

装备有盘形滚刀的滚筒刀盘，如图2所示，刀盘整体向前推进速度v，同时，滚筒绕其自身轴线滚动转速n(rpm),则滚刀中心运行的轨迹为长幅摆线。图中R0为滚刀中心分布圆半径；θ为滚刀中心转角。

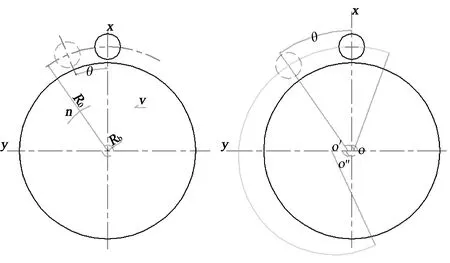
图2 滚筒参数及形成长幅摆线示意

该长幅摆线的基圆半径Rb为：

Rb=v/n(mm)

2.1 滚刀中心轨迹曲线

以滚刀位于图示x轴位置时刀盘中心位置O为原点，建立图示坐标系,对于任何一个转角θ，滚刀中心坐标为(x,y)，滚筒中心移动到(x0,y0)：

此时，滚刀中心坐标(x,y)，滚刀中心轨迹为长幅摆线，曲线参数方程为：

(1)

此时滚筒的速度瞬心位置O″坐标为(-Rb，Rbθ)。

2.2 滚刀刀刃包络曲线函数

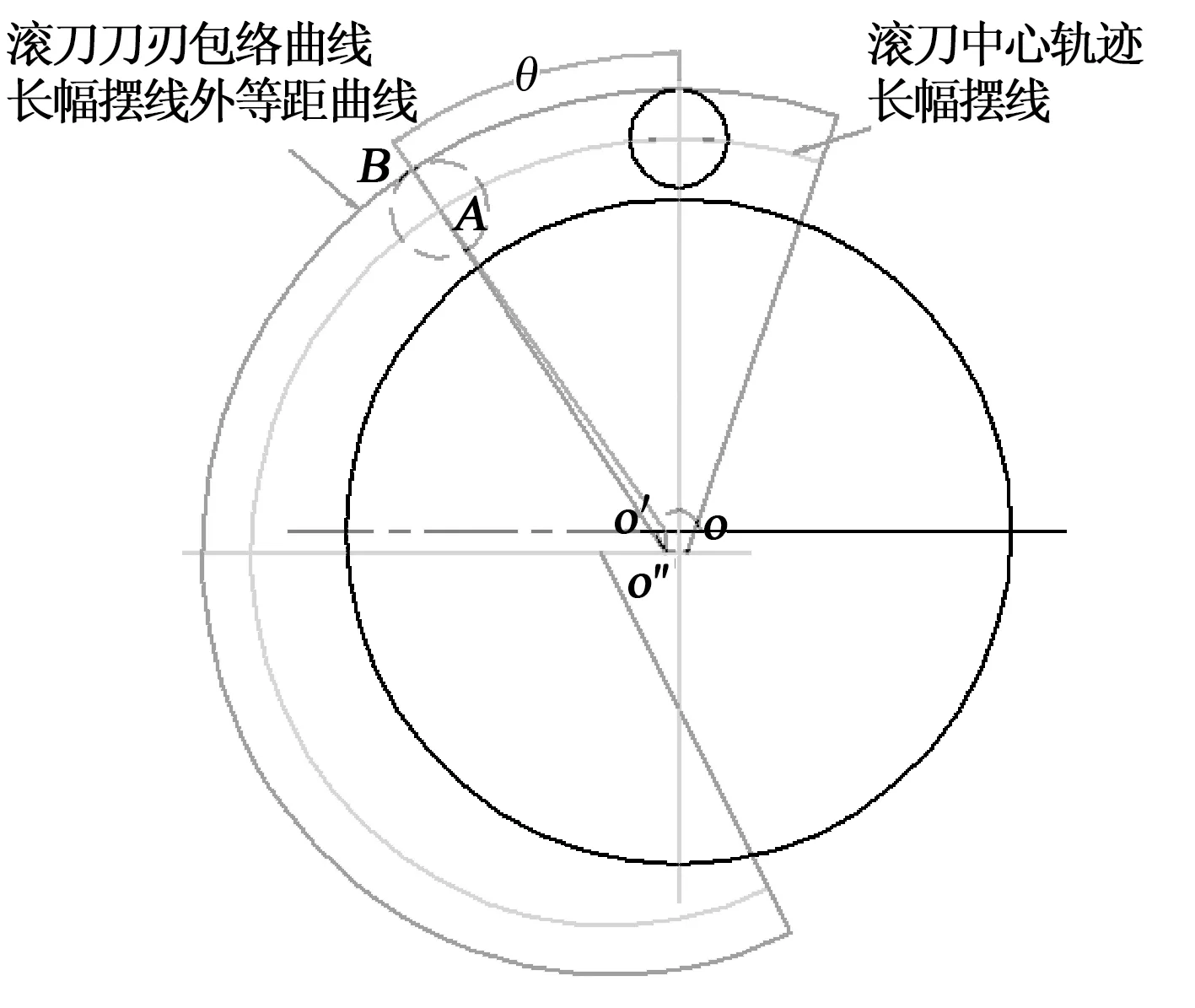
图3 长幅摆线的外等距曲线

沿长幅摆线的法线方向向外延伸盘形滚刀半径R，及达到外等距曲线上的点B，可以推出长幅摆线外等距曲线的参数函数。

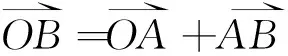
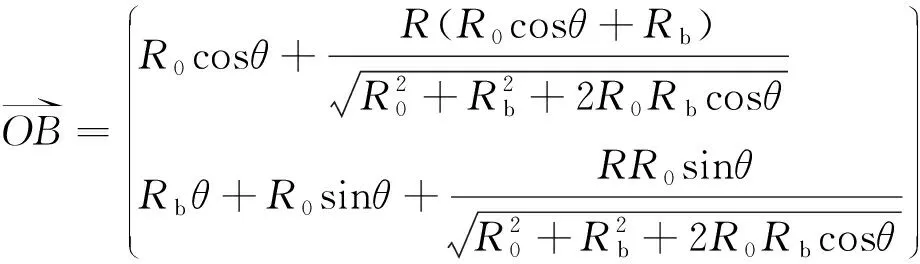
(2)

2.3 两条有相位差的等距曲线的交点

图4为两条等距曲线交点。

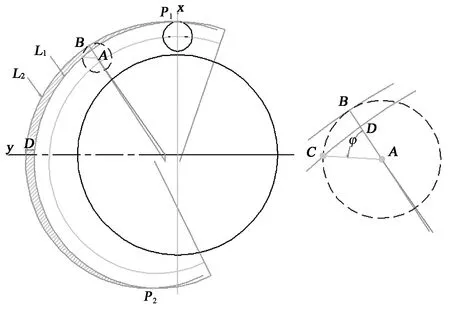
图4 两条等距曲线交点

如图4所示，y向距离为D(D≠0)，图中2条等距曲线的参数方程为：

L2：

两条曲线相交，x坐标相等，则有：

可以得出：

cosθ=cosφ

φ=2kπ±θ

y坐标相等，有：

显然，θ=-φ或θ=2π-φ，代入上式，有：

或

即，交点P1的y坐标为D/2，交点P2的y坐标为πRb+D/2，所对应的滚刀转角分别为θ1和θ2。从图4可以清楚地看出，对于安装盘形滚刀的滚筒形刀盘，只有进入到点P1和P2对应的相位之间的位置才能切削到岩石，如图示阴影部分。

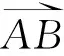
p=|AB|，φ=∠CAB

在确定同一截线上相邻两滚刀的相位差后，滚刀的截割深度p和接岩角度φ仅和盘形滚刀的相位相关。

3 装备盘形滚刀的滚筒刀盘的力学分析

3.1 不同截线上装备盘形滚刀滚筒刀盘力学分析

图5为装备盘形滚刀的滚筒刀盘的力学模型，为简化起见，滚筒上仅画出2条截线，2条截线距离S。如有多条截线，分析方法相同，并得出相同的结论。

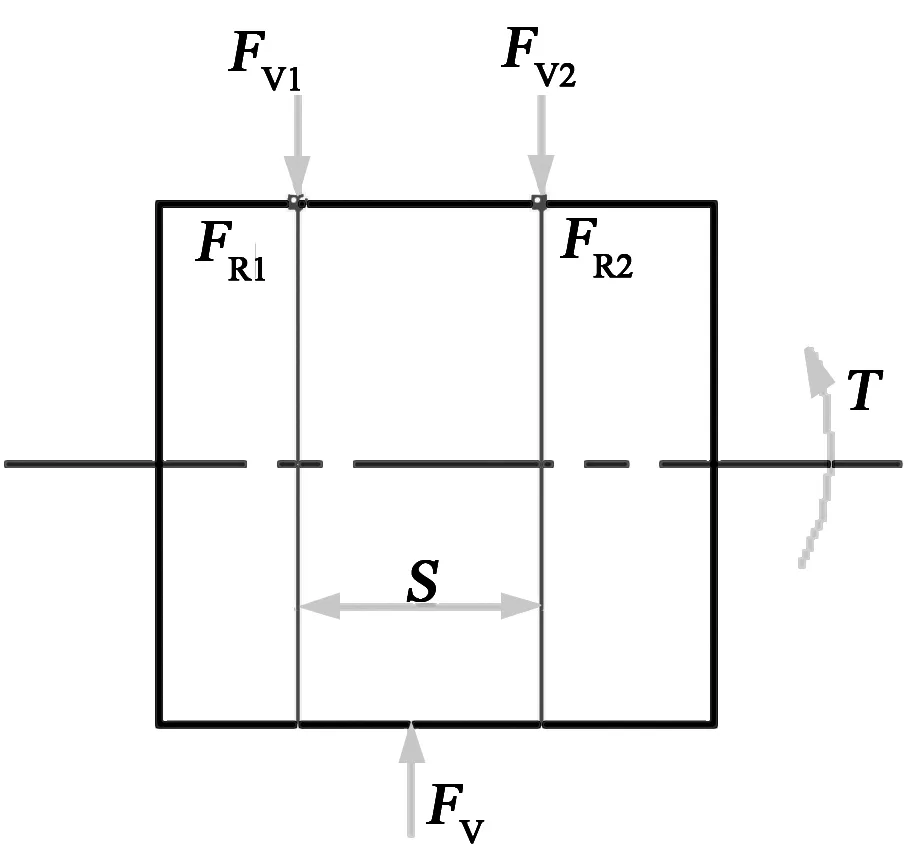
图5 不同截线盘形滚刀受力分析

破岩时，岩石对滚筒上不同截线上的盘形滚刀的径向力为FV1和FV2，切向力分别为FR1和FR2，为平衡岩石的作用力，需要给滚筒推进油缸一推力FV和驱动力矩T。

FV=FV1+FV2

T=FR1R+FR2R

从以上推理可以看出，滚筒的推力FV和驱动力矩T跟滚刀在滚筒轴向的位置分布没有关系。所以，在以下对滚筒的力学分析过程中，把不同截线上的滚刀放在同一截线上分析，不会影响滚筒的力学分析结果。

3.2 同一截线不同相位滚刀切削几何特性分析

在滚筒的同一截线的不同相位上布置滚刀，如图6所示，盘形滚刀中心轨迹是长幅摆线(见2.1所述)，基圆半径Rb。根据式(2)，滚刀1切削轨迹为：

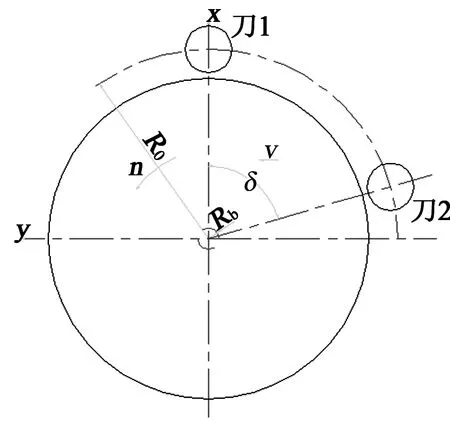
图6 同一截线滚刀力学分析

当滚刀2到达图示滚刀1的位置时，滚筒刀盘整体向前移动的位移D为：

D=Rbδ

滚刀2在滚刀1切削轨迹的基础上，切削出新的轨迹：

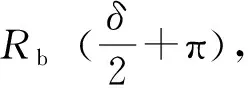
3.3 基于CSM模型的滚筒刀盘力学分析

根据3.1所述，装备盘形滚刀的滚筒刀盘破岩需要的推力和驱动转矩和盘形滚刀所处截线的位置没有关系。为简化起见，把所有盘形滚刀集中于一截面上，建立刀盘的数学模型(图7)。

图7中，刀盘整体推进速度v,绕自身轴线旋转转速n(rpm)。在设计中，为使得刀盘运转过程中均匀转动，不受滚刀离心力的影响，滚刀均匀布置，相邻两截线的刀间距为S，刀刃宽度T，滚刀半径R。图中所示滚刀可以代表几个滚刀的叠加。一般情况下，滚筒刀盘有2个自由度：y向(可以前后整体运动)和绕轴向旋转。破岩过程中，为平衡岩石对滚筒的反力，需要对滚筒沿y向的推力FΣ和沿转动方向的驱动转矩TΣ。

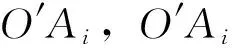
Pi=|CiBi|，φi=∠BiAiDi

这2个参数仅和滚刀转角θi相关。

据第1节所述，滚刀i受到岩石的总反力Fti和方向角δi为：

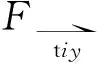
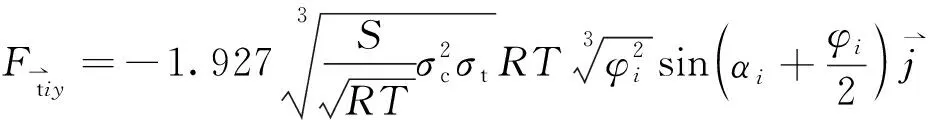
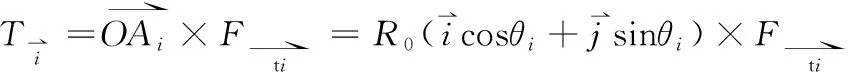
(3)

(4)

式中，θi[θ1，θ2]，θ1和θ2的定义见2.3节所述。

4 结 论

(1)本文建立了装备盘形滚刀滚筒刀盘的数学模型，通过对该数学模型的分析，得出了滚筒刀盘盘形滚刀切削的轨迹为长幅摆线的外等距曲线，并推出了该曲线的参数方程。

(2)通过对外等距曲线的几何分析，结合实际应用，给出了滚刀在任意角度的重要切削参数截割深度和接岩角度的数学解释。

(3)基于CSM模型，推出了滚筒刀盘破岩时的推力和驱动转矩公式，为计算机程序解题提供了数学依据，可为滚筒刀盘的设计及实际施工力学预测提供科学指导。

本文对滚筒刀盘进行了深入的数学分析，仅加入了切削过程中所需要的正滚刀，实际应用中还有边滚刀等其他刀具，在本文中没有涉及；另外，本文中所用到的CSM力学模型，用到了线性压力分布。文中所推出的力学公式，还有待进一步的试验验证。