圆的对称性等价性研究及分类标准探索

湖北省赤壁市第一初级中学(437300) 李道生

湖北省赤壁市实验中学(437300) 叶应忠 吴海林

圆是轴对称图形,过圆心的任何一条直线都是它的对称轴.因此,圆的轴对称性超越一切平面图形,达到了平面图形轴对称性的最高境界,即轴对称到不能再轴对称了.

圆不仅是中心对称图形,而且独具旋转不变性(绕圆心旋转任意角度都能与原图形重合).因此,圆的中心对称性无与伦比,达到了平面图形中心对称性的最高境界,中心对称到不能再中心对称了.

总之,不论是圆的轴对称性还是圆的旋转不变性,都具有举世无双、独一无二、登峰造极的特点.

因此,圆的两大对称性的对称程度不存在谁强谁弱,而是平起平坐、不分上下,于是猜想这两大对称性应是等价关系(以美起真),其猜想的思维过程如下:

若曲线C为圆,则过定点O(即圆心)的任—条直线皆为曲线C(即圆)的对称轴;反之,由圆的轴对称性的独一无二性,我们猜想:若过某定点O的任一直线,皆为某一条封闭曲线C的对称轴,则曲线C为圆.

于是有:过某定点O的任—直线,皆为某一条封闭曲线C的对称轴⇔曲线C为圆.

若曲线C为圆,则曲线C绕某定点O(即圆心)旋转任意角度皆与本身重合;反之,由圆的旋转不变性的独一无二性,我们猜想:若曲线C绕某定点O旋转任意角度皆与本身重合,则曲线C为圆.

于是有:曲线C为圆⇔曲线C绕某定点O旋转任意角度皆与本身重合.

综合有:过某定点O的任—直线,皆为某一条封闭曲线C的对称轴(轴对称性)⇔曲线C为圆⇔曲线C绕定点O旋转任意角度皆与本身重合(旋转不变性).因此:圆的轴对称性⇔圆的旋转不变性.

由此,我们作出如下预测:

预测1“圆的轴对称性与圆的旋转不变性是等价的”.即圆的两种最高境界的对称性,内部是和谐统一的,是圆的同一本质的两种不同表现形式.

因此,作为反映圆的轴对称性的垂径定理与作为反映圆的旋转不变性的圆心角、弦、弧、弦心距之间的关系定理应具有等价关系,应可互相证明,即:

预测2垂径定理⇔圆心角、弦、弧、弦心距之间的关系定理

事实确实如此,我们既可由垂径定理推出关系定理(“圆心角、弦、弧、弦心距之间的关系定理”,简称为“关系定理”),也可由关系定理推出垂径定理(注意,我们是不利用“圆的定义”的前提下,两个定理的互推).

1、垂径定理→圆心角、弦、弧、弦心距之间的关系定理

如图1,已知∠A′OB′=∠AOB,OE⊥AB,垂足为D,E在⊙O上,OE′⊥A′B′,垂足为D′,E′在⊙O上,求证:弧AB=弧A′B′,AB=A′B′,OD=OD′.

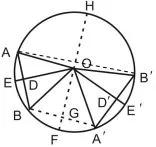
图1

证明因为,OE⊥AB,垂足为D,E在⊙O上;OE′⊥A′B′,垂足为D′,E′在⊙O上.所以,AD=DB,A′D′=D′B′(垂径定理),所以,OA=OB,OA′=OB′(线段垂直平分线的性质).连接A′B,过圆心O作FH⊥A′B交⊙O于F、H两点,垂足为G.则A′G=GB,弧A′F= 弧FB(垂径定理),故△A′OG～=△BOG,∠A′OG=∠BOG,OA′=OB,从而,OA=OB=OA′=OB′.又 ∠AOB= ∠A′OB′,所以,△AOB～=△A′OB′,AB=A′B′,OD=OD′. 因为,∠A′OG= ∠BOG,∠A′OB′=∠AOB,所以,∠HOB′= ∠HOA.连接B′A,因为,OB′=OA(已证),所以,OH⊥AB′(等腰三角形三线合一),所以,弧B′H=弧AH(垂径定理).因为,FH为⊙O的直径,所以,弧FB+ 弧BA+ 弧AH= 弧FA′+ 弧A′B′+ 弧B′H(圆的轴对称性,实质是垂径定理).因为,弧FB=弧FA′,弧AH= 弧B′H(已证),所以,弧AB= 弧A′B′.

2、圆心角、弦、弧、弦心距之间的关系定理→垂径定理

图2

如图2,已知,AB为⊙O的弦,直径EF⊥AB于D,交⊙O于点E、F,求证:AD=DB,弧AF=弧FB,弧AE=弧BE.

证明连接OA、OB,作∠AOB的平分线OF′交⊙O于F′,交AB于D′,连接AF′,BF′,作OG⊥AF′于G,OH⊥F′B于H,设OF′的反向延长线交⊙O于E′,则弧AF′= 弧F′B,AF′=F′B,OG=OH(关系定理),又∠AOE′= ∠BOE′(平角定义),所以,弧AE′=弧BE′(关系定理).在 Rt△OGF′与 Rt△OHF′中,因为,OG=OH,OF′为公共边,所以,Rt△OGF′～=Rt△OHF′,所以,∠OF′G=OF′H,又AF′=BF′(已证),D′F′为公共边,所以,△AF′D′～=△BF′D′,所以,AD′=BD′,∠AD′F′= ∠BD′F′=90°,即OF′为AB的垂直平分线,所以,OA=OB,所以,OD与OD′重合(等腰三角形三线合一),从而,F与F′重合,E与E′重合.故EF与E′F′重合,因为,AD′=BD′,弧AF′= 弧F′B,弧AE′=弧BE′(已证),所以,AD=BD,弧AF=弧FB,弧AE=弧BE(F与F′重合,E与E′重合所致).

具体尝试,验证猜想,发现果真如此时,其带给我们思维的愉悦造成心灵的震憾将无以复加.如若只死记套用,绚丽多姿的圆将失去其夺目的光彩.

可见,圆的轴对称性与中心对称性达到极致后实现了统一,至此,还从未见过那位老师考虑过圆的两类对称性(及其代表性定理)之间的等价关系,更谈不上有心用圆的轴对称性圆的旋转不变性.而是按传统惯常的认识,认为圆的性质分为两大类,—类反映圆的轴对称性(由圆的轴对称性或垂径定理进行证明);一类反映圆的旋转不变性(由圆的旋转不变性或关系定理进行证明).圆就是通过两大对称性来发号施令、引领众生,据此编制知识结构网络图如下:

根据上面研究的圆的轴对称性与圆的旋转不变性的等价关系的预测,再来分析如上编织的圆的知识结构网络图,就会产生如下疑问:圆的任一性质若可由轴对称性推出,则也可由旋转不变性推出,反之亦然.那么,圆的性质若可看作反映圆的轴对称性,则也可看作反映圆的旋转不变性.因此,划归轴对称之列的性质也可划归旋转不变性之列,反之亦然.即圆的两类对称性质是统一的,并没有绝对的分界线.

那么,上面圆的知识结构网络图划归的依据是什么?我们常说某性质反映圆的轴对称性,某性质反映圆的旋转不变性是什么原因?是根据证明该性质时使用的轴对称性或是旋转不变性为依据来划分的吗?如此看,根据圆的轴对称性与圆的旋转不变性的等价性,用圆的轴对称性证明的性质也可用圆的旋转不变性来证明,那么,划归轴对称性之列的性质也可划归到旋转不变性之列中去,反之亦然.究竟划归的依据是什么?

我们认为,划分标准应是如下两个方面:一是根据性质的证明是采用的圆的轴对称性或是圆的旋转不变性来划分(注意,证明选择圆的轴对称性或是圆的旋转不变性,要以自然简单为准),二是根据与性质相关的几何图形的形态呈轴对称性还是旋旋转不变性特征来划分.

总之,是根据图形的外形特征及性质之间的相互演变关系来划分的.如此分类处理,有利于对圆的性质的直观性认识,有利于绘制条理清晰的知识结构网络图,反映圆的性质的内在对称性及外在结构对称性的关系.

如“圆的两条平行弦所夹的弧相等”,其外形特征给人一副轴对称的形象(见下图3),所以划分为轴对称性之列更贴切些(另外,从证明方法上看,用“垂径定理”证明比用“关系定理”证明更自然简单,也更符合图形的结构特征).

又如,“同圆半径相等”是圆的定义的直接反映,圆的两大对称性皆是由其推出,那么,“同圆半径相等”划分为何种对称形式中更为合理呢?由于点的旋转不变性反映的就是同圆半径相等,且“同圆半径相等”的动态特征呈旋转状(见下图4),因此,“同圆半径相等”划为旋转不变性之列是自然而然的事.

再如,由垂径定理可演变出切线性质定理,而垂径定理反映圆的轴对称性,由此,我们将切线性质定理及推论划归于“轴对称性”之列.

另如,由圆周角定理可演变出弦切角定理,而圆周角定理由同圆半径相等推出,同圆半径相等反映圆的旋转不变性,故圆周角定理及弦切角定理划归于“旋转不变性”之列.再看圆周角定理的推论“同弧所对的圆周角相等”,也给人一副施转的架式(见下图5),说明这样划归是合适的(注:弦切角定理证明中利用了切线性质定理,因此弦切角定理的划分,不应是单纯的划分在圆的旋转不变性之列中,而应放在反映两类对称性统一的地方,即圆的知识结构网络图应分三部分.这样,编织的圆的知识结构网络图,才更清晰的看出圆的性质的演变关系).

图3

图4

图5

弄清圆的对称性的分类标准,并以此绘制圆的性质相互演变关系图,有利于掌握圆的性质的内在规律性及看清各性质之间的来龙去脉.

圆的定义是两大对称性的根源,两大对称性都是用圆的集合定义进行证明,它们统一于圆的定义中,两大对称性是圆的定义的具体形象反映,是圆的本质特征的两种表现形式.

总之,圆的定义是圆的性质之源,反映圆的定义的形象特征是圆的两大对称性,以此为发端,强强联手(两类对称性的极致性)、携手前行,引出圆的所有性质定理.圆的所有性质定理依据其特点可分属两大对称性,而实质是统一的,统一于圆的定义中.圆的任意一个性质既可以说是反映圆的对称性,也可以说是反映圆的不变性,实质一样,只是说法不同.

观察圆的知识结构网络图,分析圆的性质的对称性特点,就会发现:反映圆的轴对称性的性质,主要反映圆的位置关系(特别是垂直关系)的对称性(轴对称与垂直如影随形,故轴对称反映位置的垂直关系是自然而然了);反映圆的旋转不变性的性质,主要反映几何量关系的“变中不变性”(旋转不变性与半径不变如影随形,故旋转不变性反映几何量关系的“变中不变性”是自然而然了).

我们教师,只有认识到“圆的轴对称性与旋转不变性是等价关系”,正本清源,才胸有成竹,编织出最科学的反映圆的本质特征的圆的知识结构网络图.

揭示圆的对称性的等价关系,才能在教学中高屋建瓴、高瞻远瞩,作为教师,应该深入剖析教材、钻研教材,这样才能设计出科学的符合圆的性质的本来面目的教学程序.否则,学生学到的一定是一堆模糊不清的性质零件,也许通过题海战术,学生会解答各类型的几何问题,但这并不能证明教学的成功.

(说起圆的对称性,学生马上背出轴对称性与旋转不变性,老生常谈不奇不怪,引不起内心激动的反映.我们学习知识如能深层次挖掘,挖出新意触及灵魂产生心灵震憾,进而知识升华,才能被知识内在美所感动,知识才能深入骨髓溶于血液.对圆的两大对称性,首先要感受轴对称到极致,超越一切平面图形,中心对称到极致,独具旋转不变性.再想象两大对称性皆达顶峰,那对称程度一定不存在谁强谁弱,而应平起平坐.于是猜想这两大对称性应是等价关系,可以相互推演,垂径定理与关系定理应可互相证明.当人们具体尝试验证,发现果真如此时,其内心的愉悦将无以复加、叹为观止.如若只死记套用,活生生的圆就失去了其巨大的教育价值).