雨水渗透下节理岩质边坡失稳离散元模拟

蒋明镜， 卢厚华， 王华宁， 廖兆文

(1.同济大学 土木工程防灾国家重点实验室 上海 200092； 2.同济大学 岩土及地下工程教育部重点实验室 上海 200092； 3.同济大学 土木工程学院 上海 200092；4.同济大学 航空航天与力学学院 上海 200092)

0 引言

自然界中的岩石在地质构造、自然环境、人类活动影响下会形成大量结构面(包括裂隙、节理和断层)，结构面的性质对岩石力学特性有着重要的影响，岩质边坡的稳定性主要受岩体中结构面的控制，表现为岩体中结构面的扩展、相互影响直至贯通破坏的演化过程[1].

目前，节理岩体边坡稳定性分析方法主要有传统极限平衡分析法，如Bishop法[2]、 Sarma法[3]等.基于有限元与离散元理论的数值分析法，有强度折减法[4]、重力增加法[5-7]、塑性极限法[8]、等效连续模型法[9]等.越来越多的学者开始使用数学的方法来研究岩土工程的问题[10].随着计算机的快速发展，离散单元(DEM)法[11]以其原理简单，在不需假定土体本构模型的条件下对大变形非连续问题进行宏微观全方面破坏分析[12]的优点逐渐体现在岩土工程研究领域内，被越来越多的岩土工作者使用，成为目前流行的岩土体的数值分析方法，国内外越来越多的学者开始从微观到宏观的多尺度[13]角度来研究岩土工程的问题.

国内学者石崇等[14]研究表明，基于颗粒离散元数值模拟可为崩塌失稳边坡的稳定性研究及灾害预测提供理论依据.蒋明镜等[15]进行了节理岩质边坡的离散元数值模拟以及环境劣化因素对非贯通节理岩体强度的影响[16].贺续文等[17]使用离散元研究了节理岩体边坡的稳定性.

然而岩体边坡在长期的运行过程中，会受到雨水的影响，表现为水对岩石具的润滑软化作用，及水中化学物质对岩石的风化作用[18].因此，研究雨水影响下节理岩质边坡在水和化学风化作用下的稳定性具有重要意义.

通过采用一种新的能够考虑岩石水软化与化学风化作用的复合微观胶结模型，在离散元软件PFC2D中，建立了倾角为85°的岩石边坡，并引入3组45°顺层节理，采用重度增加法研究了其在雨水渗透下(即水软化及化学风化作用下)的应力、应变、位移及其破坏过程等演化规律.

1 岩石试样离散元模型介绍

传统微观接触力学模型[19-20]假定颗粒由单一胶结物质连接，对连接的颗粒进行复杂路径下的DEM模拟加载：纯拉、纯压、纯剪、压剪、纯扭、压扭、压剪扭等，并与室内实验、理论推导及数值模拟三者对比分析、验证[21]，得到胶结物的破坏准则.而Ciantia和Prisco等[22]对凝灰岩的研究指出凝灰岩在微观上含有两类胶结形式：沉积胶结和成岩胶结，如图1(a)所示.由于沉积胶结和成岩胶结在水及化学因素作用下的影响不同，因此在凝灰岩等软岩的基础上，本文采用更符合软岩实际微观接触的复合胶结模型[18]，其DEM微观图如图1(b)和1(c)所示，该模型能够考虑水软化和化学风化的作用.通过制备不同力学特性的沉积胶结与成岩胶结，将数值模拟、室内试验及理论分析结果相互验证得到复合胶结模型在不同荷载下的力位移关系，并将其破坏强度包线引入到离散元中即可得到考虑水软化和化学风化的复合胶结接触模型，其详细过程可参考文献[18].

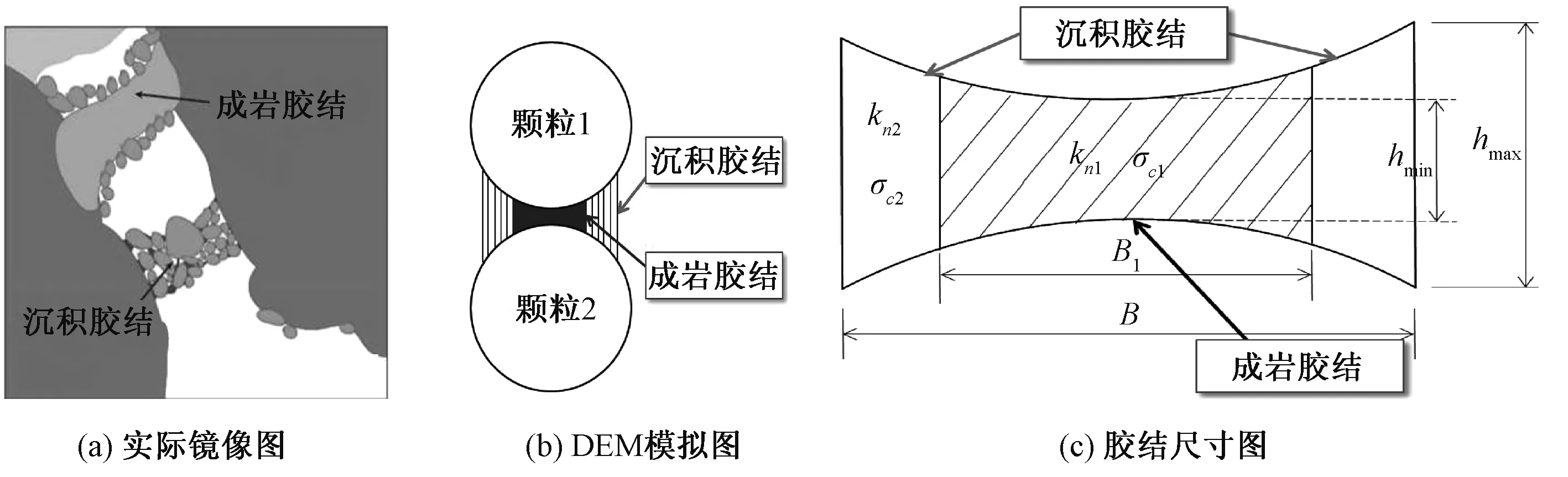
图1 岩石颗粒微观胶结DEM图Fig.1 The DEM microscopic bond graph of rock particles

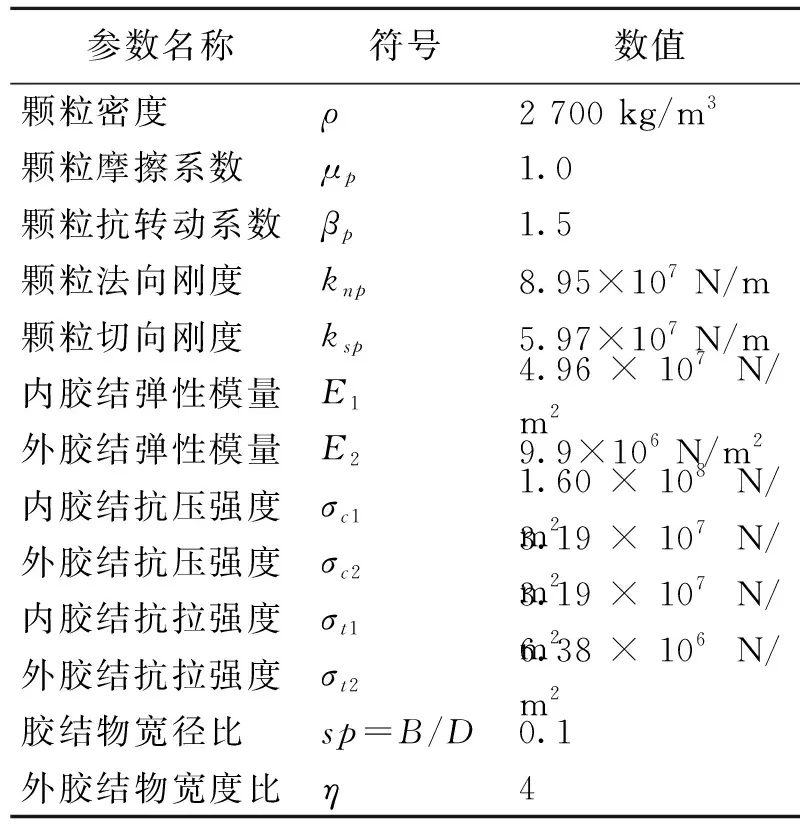
参数名称符号数值颗粒密度ρ2 700 kg/m3颗粒摩擦系数μp1.0颗粒抗转动系数βp1.5颗粒法向刚度knp8.95×107 N/m颗粒切向刚度ksp5.97×107 N/m内胶结弹性模量E14.96×107 N/m2外胶结弹性模量E29.9×106 N/m2内胶结抗压强度σc11.60×108 N/m2外胶结抗压强度σc23.19×107 N/m2内胶结抗拉强度σt13.19×107 N/m2外胶结抗拉强度σt26.38×106 N/m2胶结物宽径比sp=B/D0.1外胶结物宽度比η4

2 试样模型建立

2.1 边坡模型建立

采用分层欠压法[23]形成颗粒数目为10万的试样，由15种粒径组成，最大粒径为2.0 mm，最小粒径为0.5 mm，平均粒径为1.3 mm，不均匀系数为2.4，曲率系数为1.1,试样微观参数见表1，颗粒级配曲线如图2(a)所示.试样首先在200g的重力加速度下固结稳定，然后施加胶结，最后进行边坡成样，边坡整体形态如图2(b)所示，图中对应边坡的坡度为85°.

2.2 施加节理及测量圆的布置

试样节理形式如图2(c)所示，节理倾角为45°，连通率为0.8，节理长度为w/7(w为边坡底面的宽度),节理间距为w/10，节理宽度为10 min{ri}(min{ri}为试样中颗粒的最小直径)，详细尺寸如图2(c).节理面的力学特性与前人的参数相同[18],节理的形式为顺层岩质边坡.为测出滑动面关键点处的应力、应变变化特征，在滑动面处设置了3个测量圆，编号分别为2、3、4，同时在坡趾处也布置了一个测量圆，编号为1，跟踪测量该处的应力应变变化情况.

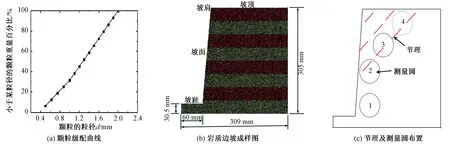
图2 DEM岩质边坡图Fig.2 The rock slope DEM graph

2.3 水软化-化学风化区域的确定

本文主要研究雨水入渗及其中所含化学物质影响下的节理岩质边坡的破坏过程，因此，必须先确定雨水的入渗规律及水软化及化学风化区域.

2.3.1雨水入渗规律 雨水入渗时，含水率随入渗深度一般分为4个区[24]：饱和区、过渡区、传导区和湿润区，其相关经验公式[25]为

hmax=139.821 9I-1.784 8t+0.091 9t2-569.942 9I2，

其中：hmax为最大入渗深度(mm)，包括饱和深度和非饱和深度；I为降雨强度(mm/min)；t为降雨历时(min).随着雨水的渗入，不同深度的岩土体饱和度也不同[26].本文借鉴前人对降雨规律的研究，从坡顶往下，在0～0.3h内，饱和度Sr≥0.45；在0.3～0.391h内，0.45>Sr≥0.30；在0.391～0.453h内，0.30>Sr≥0.15；在0.453～0.5h内，0.15>Sr≥0；0.5h以下饱和度Sr=0.此时模拟的饱和入渗深度为z0=0.3h，h为试样高度，0.45为试样的临界饱和度(试样在饱和度大于等于0.45后，力学特性基本与饱和度为1.0时一样，因此这里仍然遵循临界饱和度的概念).

2.3.2化学风化规律 Yokota和Iwamatsu[27]指出边坡岩体的风化程度随深度的增加大致线性减小.本文在模拟时，化学风化因素所影响的区域假定只局限于含水饱和区，在饱和入渗深度z0处，质量损失率为0，因此，距坡顶距离为zw高度处的质量损失率αw为：从坡顶向下，在0～0.12h内，0.5>αw≥0.3；0.12～0.18h内，0.3>αw≥0.2；0.18～0.24h内，0.2>αw≥0.1；0.24～0.3h内，0.1>αw≥0；0.3h以下部分，αw=0.

3 模拟结果及分析

Chen和Mizuno[5]、Seo[6]、Swan 等[7]的研究结果表明重力增加法在计算边坡的稳定性是可行的，本文重力加速度从200g逐渐增加，每增加一步重力加速度，观察其在特定的重力作用下是否会破坏，进而判断其稳定性.

3.1 破坏形态

图3为45°节理岩质边坡在250g的重力场中发生失稳滑动破坏过程中的边坡形态、力链及胶结破坏演化图.由图3(a)可以看到，边坡首先沿第3节理滑动并引起岩桥的破坏贯通，形成滑动面，使得上覆岩层沿着滑动面向下滑动，第2、第1节理处的岩桥依次贯通破坏.图3(b)为边坡在破坏过程的力链演化形态，在整个破坏过程中，不同位置处都有力链集中的现象发生，在第3节理处，力链集中现象更加明显，力链的集中形式不断变化.图3(c)为粒间胶结破坏图，从图中可以看到每个节理都有胶结破坏，但是第3节理胶结破坏的数目较多，首先形成滑动面.

3.2 应力应变等信息分析

图4(a)为胶结破坏数目随循环步数的变化图.胶结破坏数目在步数为275万步后有个短暂的增加，之后有个短暂的平稳，随后又继续快速增加.同时从破坏类型上可以看到，在边坡破坏阶段，压剪扭破坏数目要略多于拉剪扭破坏数目，但是拉剪破坏速率大于压剪破坏速率.随着循环步数的增加，到滑动阶段，可以明显看到拉剪扭破坏数目增长较快.

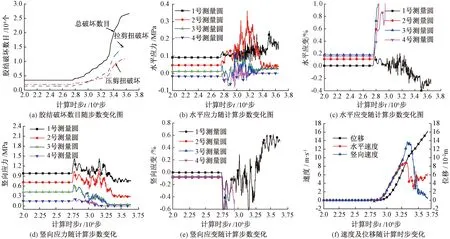
图4 微观信息图Fig.4 The micro information graph

图4(b)和(c)分别为测量圆处的水平应力及水平应变.从图4(b)中可以看到，从275万步开始水平应力开始逐渐波动.在290万步之前，应力波动幅度较大，但频率较小，结合图4(f)可以推测，边坡刚开始滑动，在290万步之后，应力的变化幅度及频率都大大增加，这是由于滑动体在滑动面上滑动引起的.其中3号和4号测量圆测得的水平应力开始为压应力，然后逐渐变为拉应力，最后变为非常小的压应力，这是因为在滑动前试样在重力作用下产生水平压应力；随着边坡的滑动，应力重新分布，由于滑动产生的拉应力会大于重力产生的水平压应力；最后滑动结束后，滑动产生的拉应力消失，坡顶位置的水平方向再次受压；1号和2号测量圆的水平应力一直为压应力，1号位置的水平应力比2号的要稍大，这是因为在坡趾附近有压力链集中，且1号位置比2号位置更偏于底部，受到的竖向压力也较大引起的.从图(c)可以看到，水平应变同样从270万步开始波动，2～4号测量圆应变为正，1号测量圆应变先正后负.

图4(d)和4(e)为竖向应力、应变随计算时步的变化图.从图4(d)中可以看到，竖向应力均为压应力，并且随着深度的增加而不断增加，表明竖向应力主要受重力场的影响.同样从270万步开始波动，且不同深度处的应力波动的规律比较相似，对比图4(f)可以发现在滑动的过程中压应力均远远大于初始的压应力，最后趋于稳定时候，均小于初始的压应力.图4(e)中竖向应变在2～4号测量圆处为负值，这与坡面向下滑动相关.1号测量圆开始受到滑动体的影响为负，后期在稳定的时候变为正值，这是因为滑动体滑动脱落，表现出卸载的情况.

图4(f)中，给出了边坡发生滑动时滑动体的水平速度与竖向速度的变化情况.从图中可以看到滑块水平速度在290万步时候开始波动，对比应力应变快速变化的270万步，速度明显变化的时刻晚于应力应变快速变化的时刻.水平速度从0开始，很快增加到峰值，然后马上跌落，之后速度值在较小值的范围内轻微波动；竖向速度与水平速度一样，竖向速度值极快地达到峰值，之后很快回落.对比水平速度及竖向速度可以发现，竖向速度的峰值约为水平方向速度峰值的1.5倍，速度变化的过程恰好对应图3(a)中边坡滑动、撞向地面及在地面上破碎的过程.随着计算时步的增加，滑动距离不断增加，在初始滑动阶段，滑块水平距离的增加很快，而后期则增加较慢.对比图中的位移与速度，可以看到位移的快速增加的时刻晚于速度快速增加的时刻，在速度增加到一定值时候，位移才开始具有明显的增加.

3.3 安全系数

文中试样从200g逐渐加载至稳定状态，在250g时候边坡开始破坏，此时对应的重力与成样平衡时重力(200g)的比值即为边坡的安全系数，因此本文模拟的节理岩石边坡的稳定系数为1.25.

4 结论

文中通过采用一种新的能够考虑水软化与化学风化作用的复合微观接触本构，初步探究了岩质边坡在水软化及化学风化影响下的破坏过程，并分析了岩质边坡破坏过程中的微观力学特性，得出以下结论.

(1) 边坡滑动前，内部的应力应变比较稳定，滑动时，其内部的应力应变变化波动比较大，不同位置处的应力应变变化整体具有相似的规律.

(2) 对比分析位移与速度的变化图，可以看到位移快速增加的时刻慢于速度快速增加的时刻，也即在速度增加到比较明显值的时刻，位移才开始快速地增加；同时对比破坏过程水平速度与竖直速度，竖直速度的峰值大于水平速度的峰值.

(3) 通过比较滑动瞬间应力应变变化波动的时刻与速度位移的快速增加时刻可以发现，应力应变变化波动的时刻先于速度与位移快速增加的时刻.

(4) 含节理顺层岩质边坡的失稳破坏主要为节理间的岩桥贯通破坏过程，破坏面为节理滑动面.颗粒间的破坏形式主要为拉剪破坏与压剪破坏，在破坏阶段，拉剪破坏的增长率大于压剪破坏的增长率，后期变为主要的破坏形式.