数码相机检校方法及精度评定
2018-11-07李胜才
李胜才,李 禺,李 旭
(四川中水成勘院测绘工程有限责任公司,四川 成都 610072)
0 前 言
无人机航空摄影测量具有优越的机动性和灵活性,该方法已被大规模应用在大比例尺地形图的生产中,可是无人机航空摄影使用数码相机几乎都是非量测相机,因此数码相机的参数检定就成为决定成图精度的关键。虽然现在很多空三加密软件都具有带任务检校功能,但是众所周知像控点的数量以及分布情况都不能与专用检校场相比,因此要做高精度的大比例尺地形图,如1 ∶500、1 ∶1 000和1 ∶2 000地形图,应到专门的控制场进行检校,最好是室外三维控制场。
1 数码相机检校参数
非量测相机需要检校的参数包括相机主距fx、fy,像主点x0、y0,径向畸变参数k1、k2,切向畸变参数p1、p2。解求相机参数需拍摄照片,而照片的外方位元素有三个线元素,即摄站坐标XS、YS、ZS和三个角元素,即姿态参数φ、ω、κ,所以相机参数检校时需要解求的参数共有14个。
2 检校使用的数学模型
关于非量测数码相机检校的论文有很多,采用直接线性变换法DLT的很多,直接线性变换数学模型为:
(1)
其中:
hΔx= (x-x0)(k1r2+k2r4)+
p1[r2+2(x-x0)2]+2p2(x-x0)(y-y0)
Δy= (y-y0)(k1r2+k2r4)+
2p1(x-x0)(y-y0)+p2[r2+2(y-y0)2]
(2)
式中X、Y、Z——像控点物方坐标;
Δx、Δy——相机畸变差;
x、y——像控点像方坐标;
r——像点到像主点的距离(向径);
li——直接线性变换系数。
从直接线性变化模型可知,直接线性变换系数有11个,而需要解算参数只有内外方位元素共9个,因此直接线性变换系数之间存在一定的相关性,并非完全独立,所以按直接线性变换模型解算的参数精度不会很高。
而本文是采用摄影测量的最基本公式共线方程作为检校使用的数学模型。
式中ai、bi、ci——为三个角元素的方向余弦。
从式(2)和式(3)可知,数码相机检校可按泰勒级数展开式(2)和式(3),保留一次项,将共线方程线性化,按每个像控点的像方坐标和物方坐标组成误差方程式。
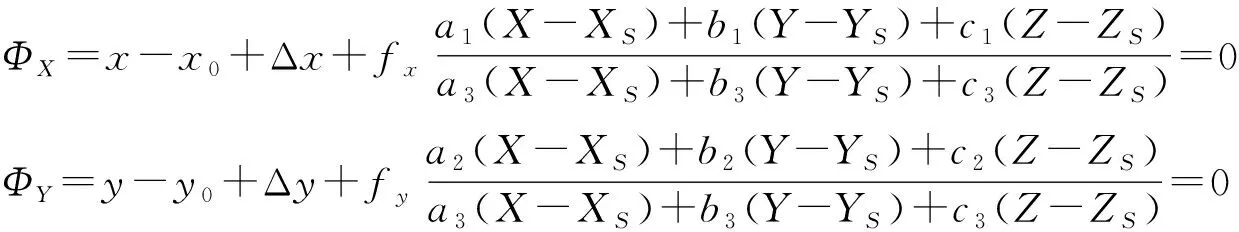
(4)
则:
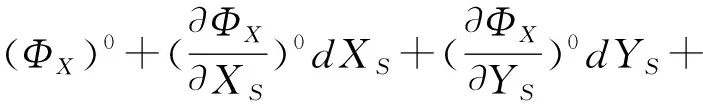
(5)
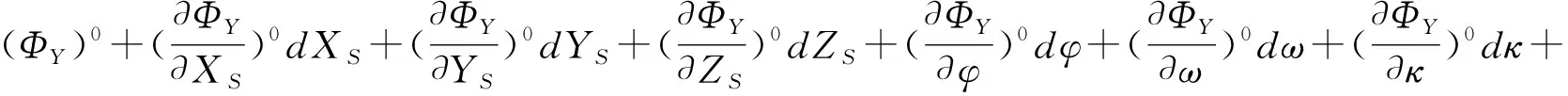
(6)
按式(5)和式(6)列出各点的误差方程,各项系数和常数项按各参数的初始值计算得到,按最小二乘法解算出各参数的改正值,采用迭代计算的方法求出各参数的最终值,因此计算的参数均为独立参数,所以只要检校场的精度满足检校参数精度要求,检定得到的相机参数均能满足相应比例尺空三加密的要求。
3 精度评定
数码相机检校完成后,可按式(4)计算各点的像方坐标改正数Vx、Vy,按式(7)计算单位权中误差。
(7)
式中Vx、Vy——像控点像方坐标改正数;
n——像控点个数。
4 算 例
2017年4月,我公司委托一家无人机公司采集某项目丘陵地区5 cm分辨率的影像数据用于1 ∶500地形图测绘,无人机公司提供的检校参数见表1。
内业空三加密时基本定向点残差平面中误差为1.2 m,高程中误差为1.9 m,根本达不到1 ∶500空三加密的精度要求。由于我公司今年3月底前已建立了高精度室外控制场,所以请无人机公司把数码相机拿到我公司的检校场拍照,进行检验,参数检验采用的像控点有78个,使用公司自己开发的检校软件计算成果见表2。
采用我公司自己检定的参数对像片纠正后,空三加密精度为基本定向点残差平面中误差为0.112 m,高程中误差为0.089 m,能够满足规范《数字航空摄影测量空中三角测量规范》(GB/T 23236- 2009)规定的1 ∶500地形图基本定向点平面中误差平地0.13 m,高程中误差平地0.11 m的要求。
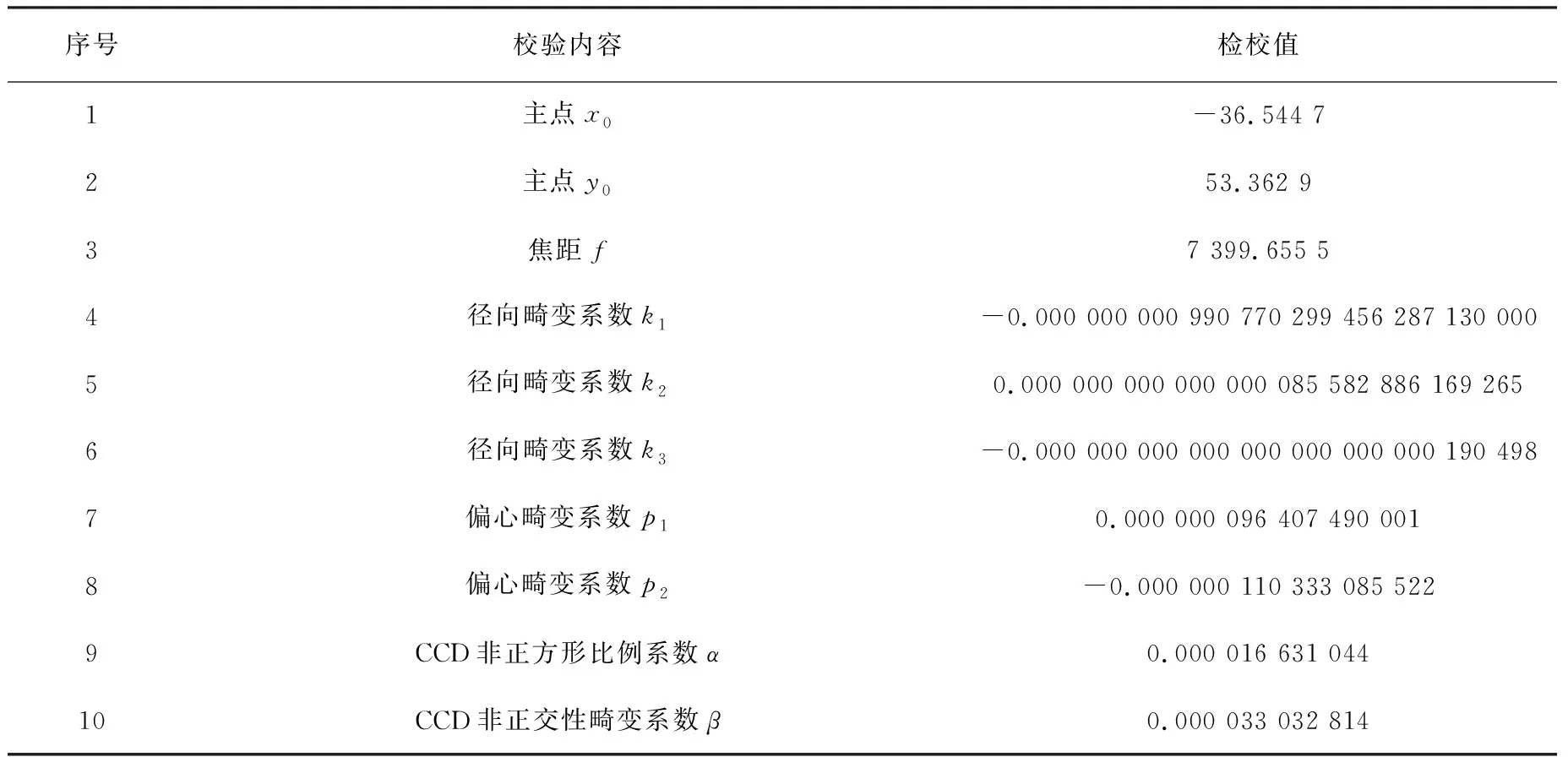
表1 数码相机检定参数
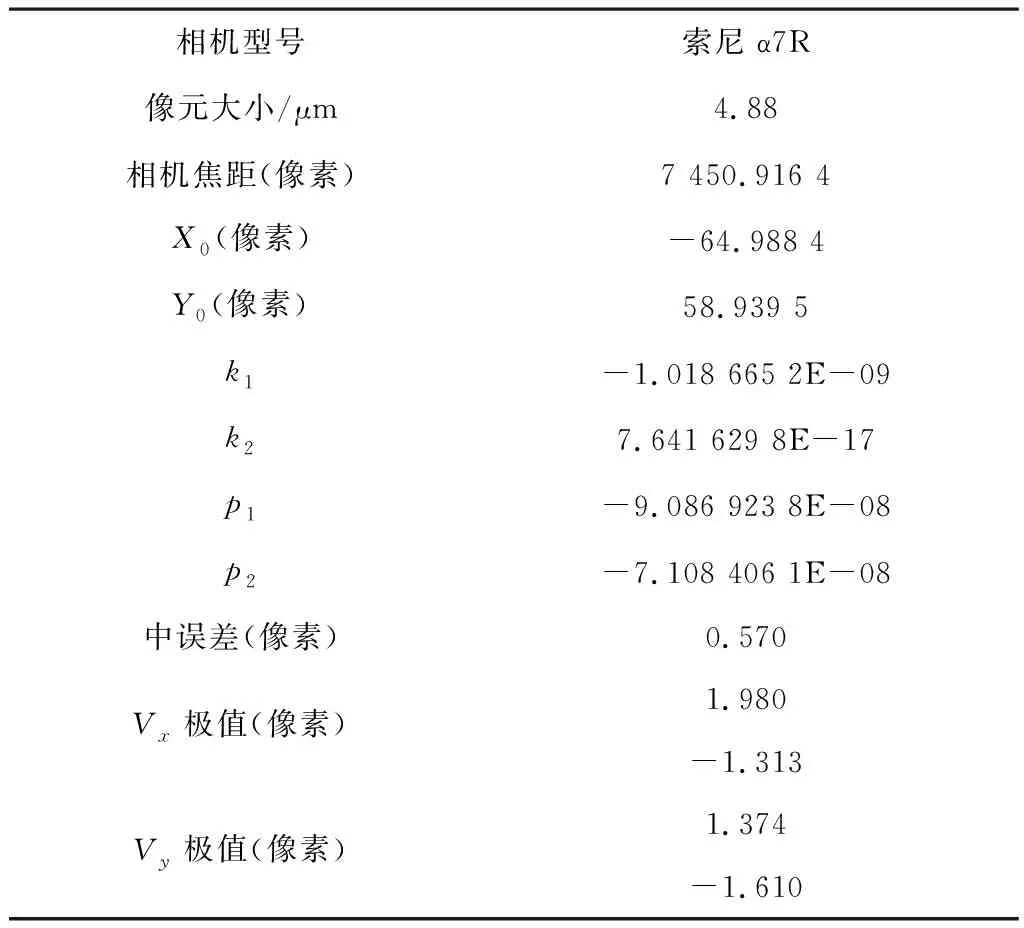
表2 数码相机检定成果及精度情况
5 结 论
(1)无人机航空摄影测量用于1 ∶500、1 ∶1 000、1 ∶2 000测图是可行的,但数码相机必须通过精确检定。
(2)用于相机检校的三维控制场按实际摄影航高放大后的像控点中误差不应大于相应比例尺像控点中误差的1/3。
(3)检校软件采用的数学模型最好是共线方程。
