下承式拱桥上无缝线路设计及纵向力影响因素分析
2018-11-07王牧麒徐金辉
谢 康,苏 谦,2,王牧麒,徐金辉,刘 宝
(1.西南交通大学 土木工程学院,四川 成都 610031;2.西南交通大学 高速铁路线路工程教育部重点实验室,四川 成都 610031;3.华东交通大学 土木建筑学院,江西 南昌 330013)
随着我国高速铁路及城市轨道交通的发展,出现了多种形式的大跨度桥型[1]。拱桥因其跨越能力大、刚度大等特点,适用于大跨铁路桥。桥上铺设无缝线路,可以减小列车动力作用,改善桥梁运营条件。虽然目前对于中小跨的简支梁和连续梁的桥上无缝线路已经有一套较成熟的计算理论,但对于拱桥这类特殊桥型桥上无缝线路的研究较少,规范中也没有相关的计算原则[2]。鉴于此,本文以下承式拱桥作为研究对象,基于梁轨相互作用原理,建立桥梁-轨道一体化的平面计算模型,并进行桥上铺轨设计,接着从桥型、荷载工况、墩台刚度等角度对桥上无缝线路附加力进行深入研究,用于指导下承式拱桥上无缝线路的设计。
1 计算过程
1.1 工程概况
以某特大桥为例,桥跨布置为3×32 m简支梁+(82+172+82)m变截面连续梁拱+3×32 m简支梁,全桥共9跨10墩,桥跨布置如图1所示。

图1 桥跨布置(单位:m)
该桥位于直线段,桥面上铺设有砟轨道,为客货双线铁路,最高轨温59.3 ℃,最低轨温-9.2 ℃,设计锁定轨温为29±5 ℃,升温时最大温差可达 35.3 ℃,降温时最大温差可达 43.2 ℃,变截面梁温差取 25 ℃。
1.2 桥上铺轨方案
方案1:全桥布置常阻力扣件。
方案2:仅拱桥2边跨布置小阻力扣件,其余地段布置常阻力扣件。
方案3:仅拱桥全长和相邻1跨简支梁布置小阻力扣件,其余地段布置常阻力扣件。
方案4:仅在连续梁左端设置1组单向钢轨伸缩调节器,尖轨位于拱桥左边跨上。
方案5:在5#桥墩处设置速度锁定器,并在主桥上布置小阻力扣件。
方案6:仅左边跨设置小阻力扣件,同时在拱桥左边跨设置1组单向钢轨伸缩调节器,尖轨位于拱桥左边跨上。
1.3 计算模型
基于梁轨相互作用原理,采用ANSYS有限元软件建立桥梁-轨道一体化计算模型。钢轨、吊杆采用Link 1单元模拟,线路纵向阻力采用线性弹簧Combin 39模拟,墩台纵向刚度采用非线性弹簧Combin 14模拟,梁体、拱肋选取Beam 54单元模拟。Beam 54具有上下节点偏移的性质,能较真实地模拟梁体与钢轨、支座与梁体之间的连接,而无需再建竖向刚臂来模拟梁体的下翼缘[3]。简化平面计算模型如图2所示。

图2 计算模型
1.4 方案比选
参照无缝线路设计规范,分别采用轨道强度、轨道稳定性、制动时梁轨快速位移、断缝值以及墩台偏心位移[4]5个检算指标对桥上铺轨方案进行检算,结果表明:方案1,2轨道强度检算不通过;方案3因铺设小阻力扣件过多,导致钢轨低温时产生的断缝值大于70 mm,检算不通过;方案4,5,6检算通过,但是由于方案4 安全系数最高,因此选择方案4作为最佳铺设方案。
2 计算结果分析
以方案4为基础,分析各纵向力。由于方案4在计算软件中有类似断轨的作用,故方案4不分析断缝值影响,而方案1断缝值检算满足要求,是工程中经常使用的方案,因此采用方案1分析断缝值。在计算过程中发现,挠曲力远小于其他附加纵向力,因此对于挠曲力不做考虑。
2.1 伸缩力
2.1.1 拱肋温差
当钢轨两端固定时,因温降和温升下钢轨伸缩力只是方向发生改变,大小不变,故仅分析温升工况。计算伸缩力时,拱肋温升为0,5,15,25 ℃共4种工况[5]。钢轨伸缩力计算结果如图3所示。
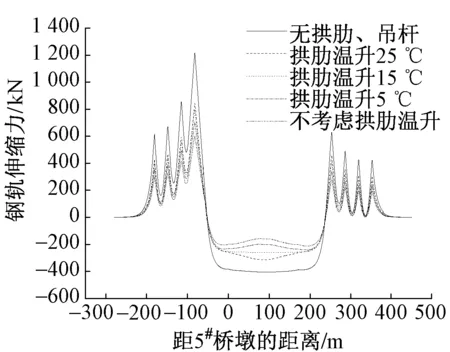
图3 不同拱肋温升下钢轨伸缩力
由图3可知,拱肋温升对钢轨伸缩力影响较大,拱肋温升25 ℃时比不考虑拱肋温升时钢轨伸缩力增大1.4倍。这主要是由于主梁在温度作用下发生纵向变形,不考虑拱肋温升时,拱肋对于主梁的变形有一定的约束,当拱肋温升为25 ℃时,拱肋与主梁同步发生伸缩变形,拱肋对主梁约束较小,钢轨伸缩力最大。
另一方面,不考虑拱肋温升时,拱肋承受的最大压力为 10 171.938 kN。随着拱肋温升增大,拱肋的压力逐渐减小,在25 ℃温升下,拱肋受拉,最大拉力为859.04 kN。
2.1.2 墩台刚度
下承式拱桥的水平纵向力可传至墩台处,因此有必要分析墩台纵向刚度对于纵向力的影响[6]。将墩台纵向刚度扩大至原来的0.5倍、1倍、2倍、5倍,钢轨伸缩力计算结果如图4所示。可知:随着桥梁墩台纵向刚度的增大,钢轨伸缩力也相应增大,但是增大幅度越来越小,因此要控制桥墩的最大刚度。同时,当6#制动墩纵向刚度减小1/2,墩台所受最大伸缩力为 2 741.9 kN,6#制动墩纵向刚度无穷大时,最大伸缩力为 5 800.2 kN。因此,为了控制钢轨伸缩力,有必要在保证安全性的基础上减少中间跨的纵向水平刚度,以满足钢轨强度的需要。
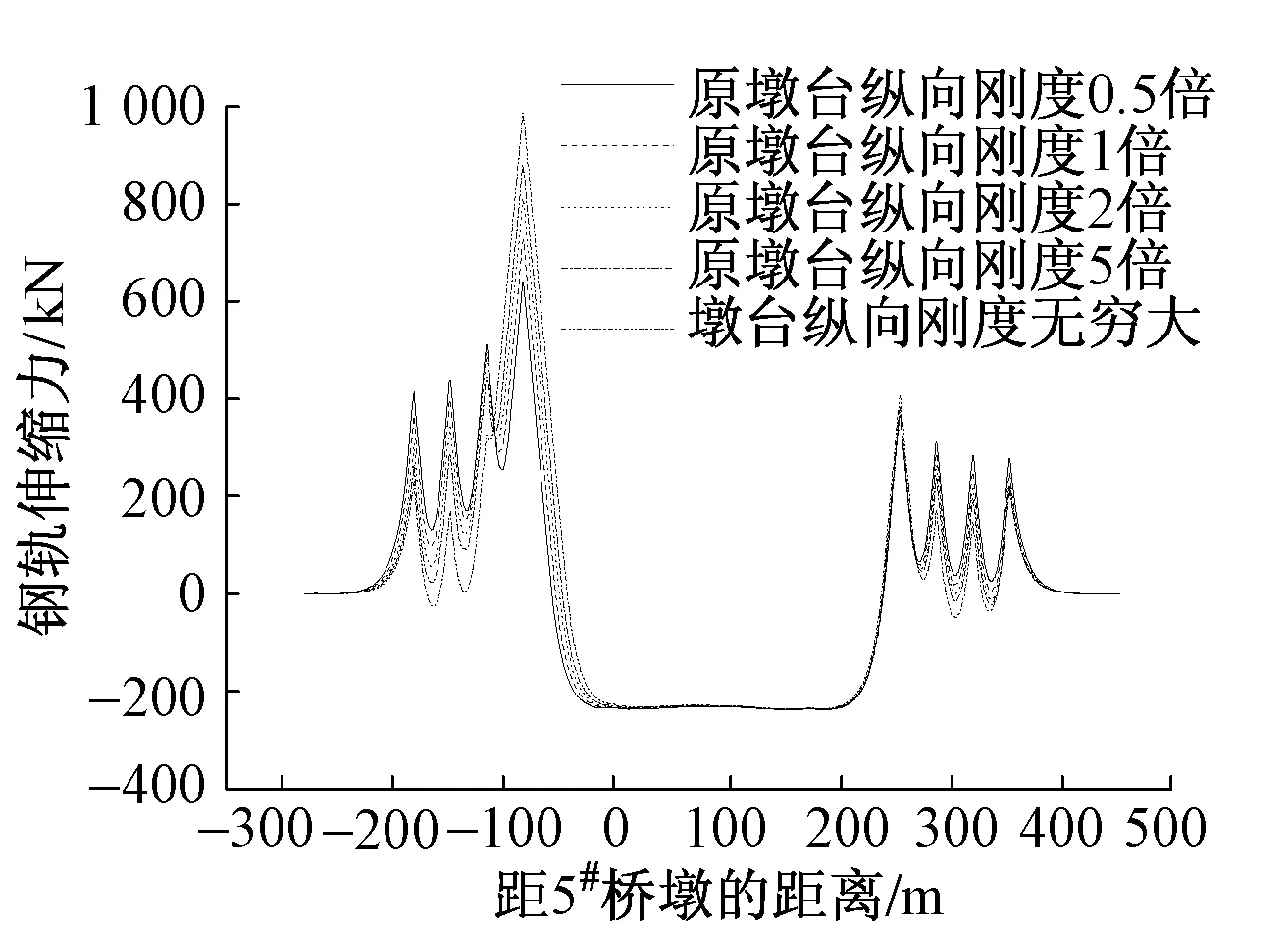
图4 不同墩台刚度下钢轨伸缩力
2.2 制动力
2.2.1 荷载工况
取列车右入桥进行分析,分别计算列车荷载分布于右端2跨简支梁(工况1)、拱桥边跨(工况2)、拱桥1/2跨(工况3)、拱桥左端拱肋处(工况4)、拱桥全跨(工况5)5种工况[4]下钢轨制动力,计算结果如图5所示。
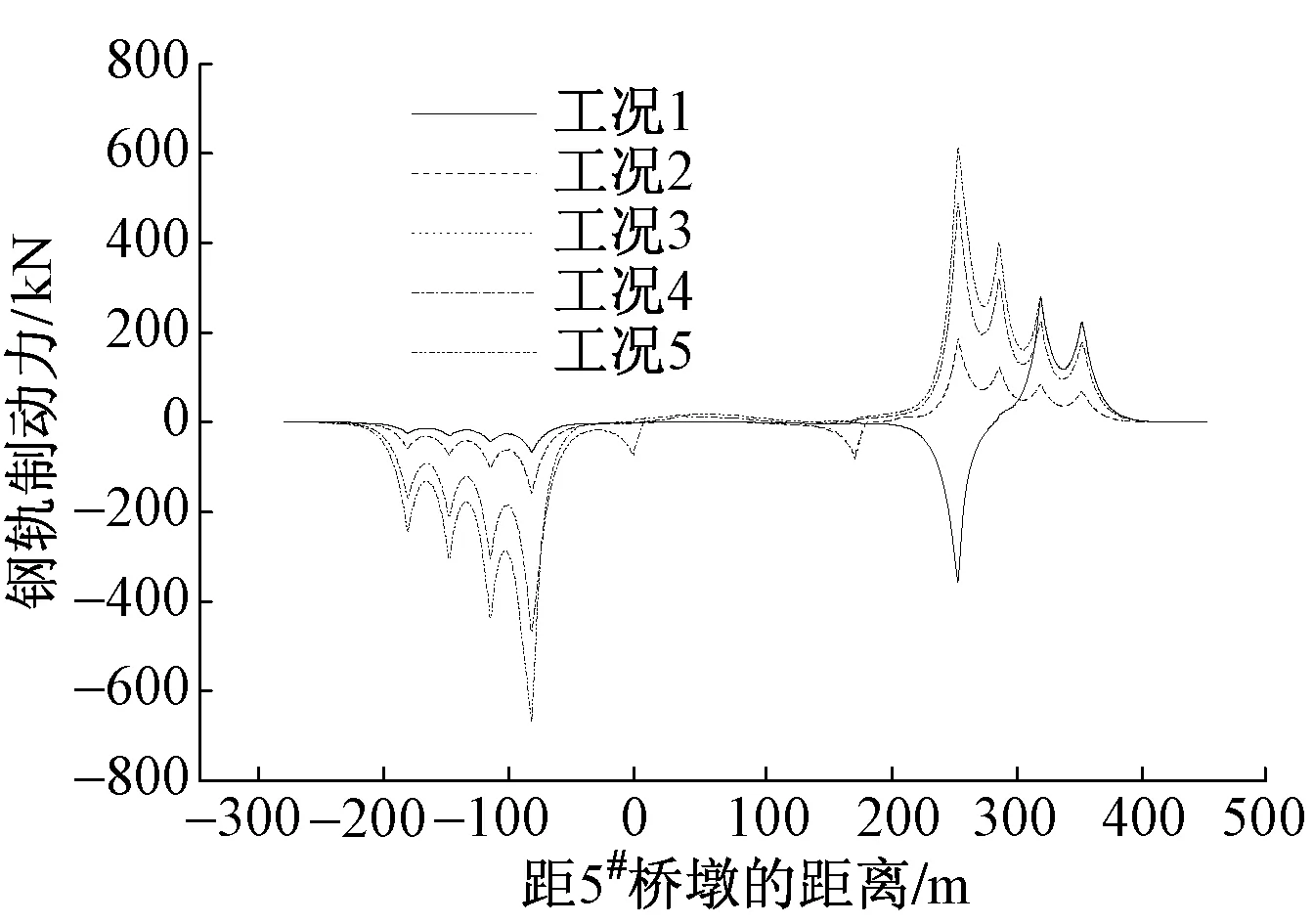
图5 不同荷载工况下钢轨制动力
由图5可知,随着拱桥上布载的区域增大,钢轨制动力也越大,其中工况5是最不利工况。因此在计算制动力时建议选取拱桥全跨布载作为最不利工况。
另一方面,工况1下拱肋承受最大拉力为280.603 kN,当主桥上布载范围增大,拱肋承受的最大压力为 2 156.098 kN。
2.2.2 拱肋
取列车右入桥分析,分别在有无拱肋和吊杆2种工况下进行计算,钢轨制动力结果如图6所示。
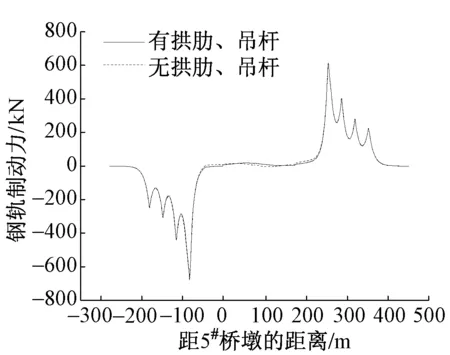
图6 有无拱肋、吊杆钢轨制动力
当不考虑拱肋和吊杆,最大制动拉力为682.451 kN,最大制动压力为618.138 kN,而存在拱肋和吊杆,最大制动拉力为667.247 kN,最大制动压力为614.2 kN。可见是否存在拱肋和吊杆对于制动力的影响不大,因此在计算钢轨制动力时,可以把下承式拱桥简化为连续梁桥,其误差在工程允许误差范围之内。
2.2.3 墩台刚度
将墩台纵向刚度扩大至原来的0.5倍、1倍、2倍、5倍,钢轨制动力计算结果如图7所示。
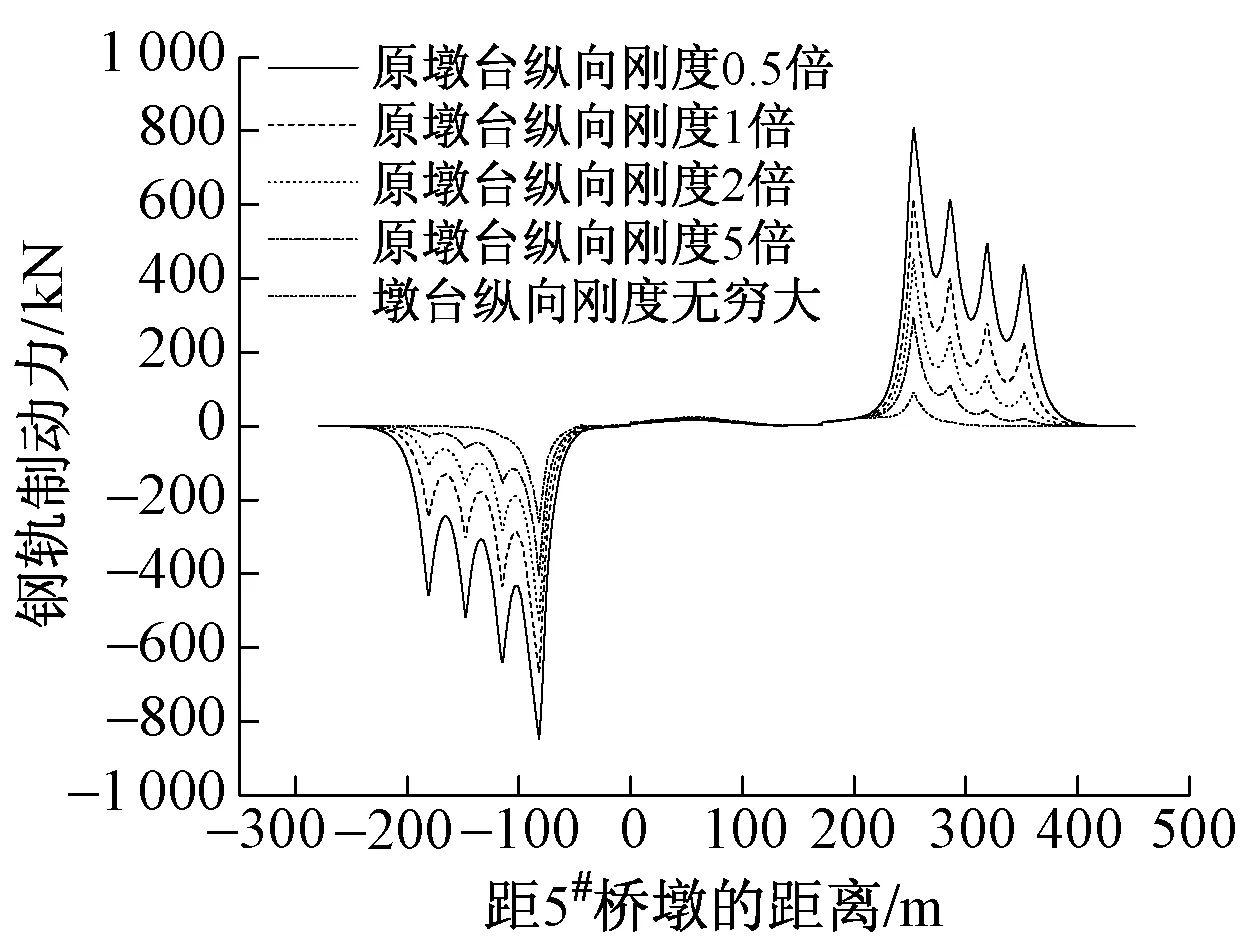
图7 不同墩台刚度下钢轨制动力
随着桥梁墩台纵向水平刚度的增大,墩台制动力由 1 037.492 kN 增大到 4 303.281 kN,但是钢轨制动力却随之减少。因此在进行桥墩设计时,要规定合理的纵向水平刚度,以防出现钢轨承受较大的制动力[7],而墩台的承载能力却没有发挥的情况。
2.3 断缝值
2.3.1 断缝位置
钢轨断缝发生位置具有很大的随机性[8],针对此类大跨拱桥的断缝值,规范没有说明。分别将断缝设置在连续梁左端(工况1′)、拱肋左起点(工况2′)、连续梁跨中(工况3′)、拱肋右起点(工况4′)、连续梁右端(工况5′)。钢轨断缝值计算结果如图8所示。
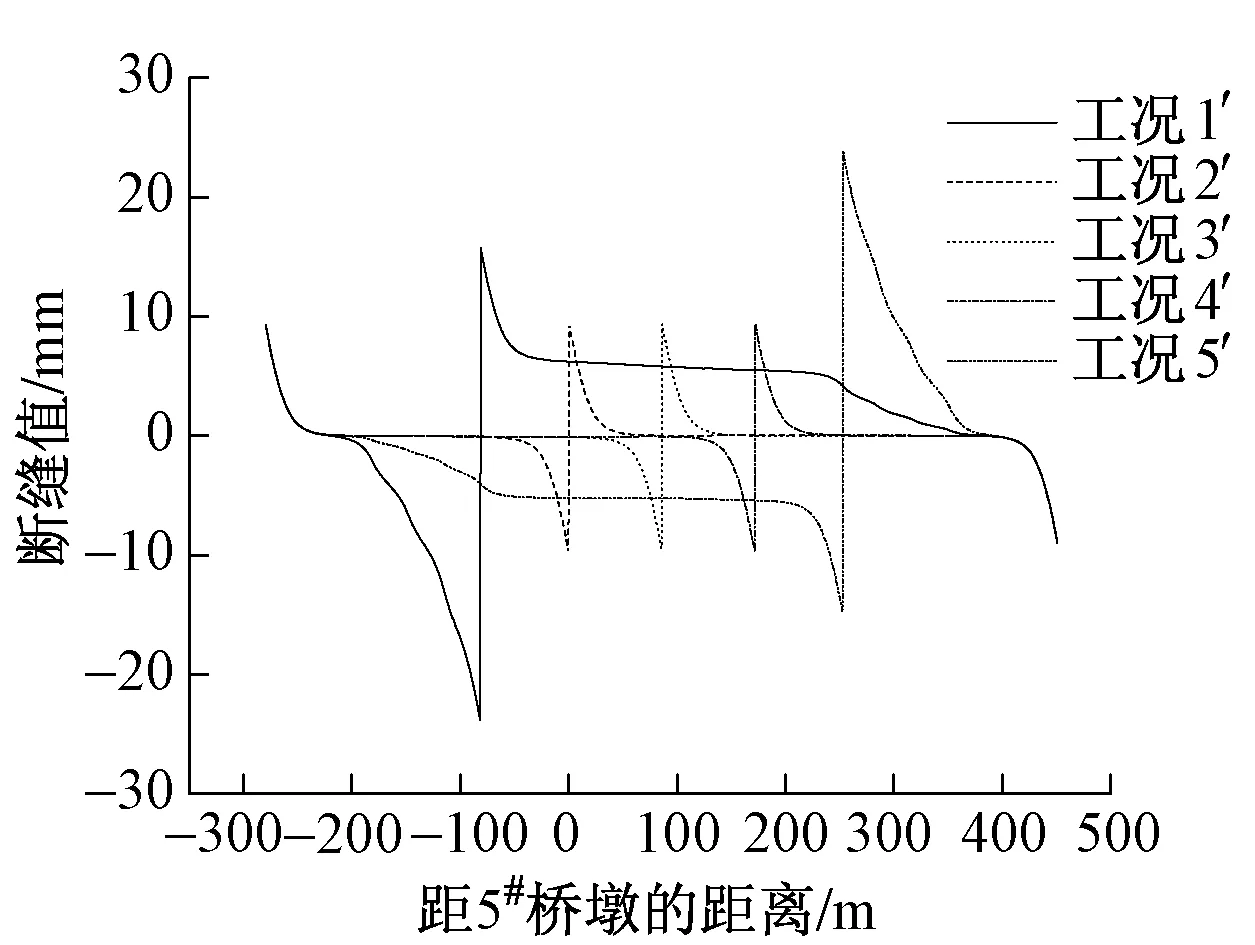
图8 不同断缝位置下钢轨断缝值
由图8可知,钢轨断缝发生位置不同,断缝值一般也不同,断缝发生在连续梁梁端附近时,断缝值最大。由于钢轨焊接不牢固的地方往往发生断缝,故需提高焊接质量,提高列车行驶的安全性[9]。
2.3.2 拱肋和吊杆
不考虑拱肋温差情况下,分析有无拱肋和吊杆对钢轨断缝值的影响,结果如图9所示。

图9 有无拱肋、吊杆下钢轨断缝值
由图9可知,拱肋和吊杆对于断缝值的影响可以忽略不计。因此在工程中可建立简化连续梁模型用于计算该桥型的断缝值。
2.3.3 墩台刚度
将墩台纵向刚度扩大至原来的0.5倍、1倍、2倍、5倍,钢轨断缝值如图10所示。
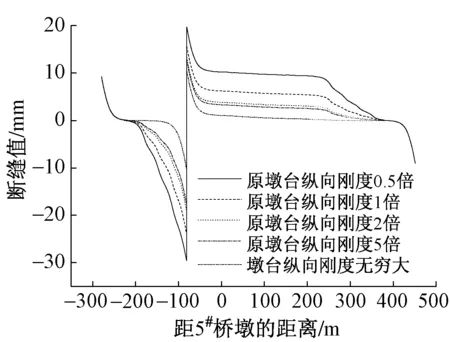
图10 不同墩台刚度下钢轨断缝值
由图10可知,随着墩台刚度的增大,对钢轨的伸缩约束作用逐渐增大,因此断缝值逐渐减小。这是设计中需要限制桥墩最小纵向刚度的原因。
3 结论
1)下承式拱桥铺轨时,建议在连续梁左端布置1组单向钢轨伸缩调节器,尖轨位于拱桥左边跨上,此时钢轨纵向附加力最小。
2)在进行下承式拱桥设计时,由于其桥上无缝线路钢轨挠曲力计算值较小,在计算中可以忽略不计。
3)拱肋温差对钢轨伸缩力影响较大,不考虑拱肋温差比考虑拱肋温升25 ℃时钢轨伸缩力增大1.4倍,因此建议计算下承式拱桥这类特殊桥型的伸缩力时,选取拱肋温升为25 ℃。
4)拱肋、吊杆对钢轨制动力和断缝值影响较小,在计算钢轨制动力和断缝值时,为简化运算,可简化为连续梁桥,其误差在工程允许误差范围之内。
5)拱肋在列车运行时,存在受拉现象,建议下承式拱桥拱肋采用钢管混凝土结构,以保证足够的受拉强度。
6)计算钢轨制动力时建议选取拱桥全跨布载工况,计算断缝时建议在连续梁梁端附近布置断轨,以在最不利组合下进行计算,且结果具有一定的安全储备。
