基于折面梁格模型的机场滑行道桥上部结构受力分析
2018-11-07孟宪锋
孟宪锋
(中国民航机场建设集团有限公司,北京 100101)
近年来航空业务量迅猛发展,受到飞机起降架次的约束,一些单跑道机场已经难以适应业务量的需求,建设第二跑道是增加机场发展空间的必要途径。考虑到新建跑道与原跑道的间距要求以及与航站楼之间的联系,通常第二跑道会规划在航站楼的另一侧,形成两条跑道分列于航站楼左右两侧的整体布局。由于跑道交叉运行的需要,通常在两条跑道之间设置联络滑行道方便飞机相互通行,这样就会造成联络滑行道与地面的陆侧交通(通常为进场路及其他交通)形成交叉。为避免飞机运行与陆侧交通发生干扰,在陆侧道路之上设置滑行道桥是一种解决办法。
滑行道桥主要为飞机提供往返运行通道。滑行道桥具有桥面宽(E类滑行道桥宽至少45 m,F类滑行道桥宽至少61 m)、移动荷载大(E类飞机最重 3 869 kN,F类飞机最重 5 960 kN)等特点。
滑行道桥上部结构通常采用整体性较好的预应力混凝土连续箱梁,截面多为单箱多室构造。对于这种宽跨比较大的箱梁,若采用单梁模型进行结构分析则不能反映箱梁的空间受力特征,难以得出各个腹板的受力情况。已经公布的JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》明确规定“弯、宽、斜及变宽或分岔等复杂混凝土桥梁结构可采用实体有限元或附录A 的实用精细化分析模型计算”。实体有限元的计算规模大,计算结果难以直接应用于设计。实用精细化分析模型具有建模方便、结果可靠、应用便捷等特点,是分析复杂混凝土桥梁结构的推荐方法。根据附录A的一般规定,滑行道桥的单箱多室箱梁结构适合采用折面梁格模型分析[1]。
梁格法已广泛应用在箱梁的设计和计算分析中,但国内研究箱梁梁格法计算的文献偏少,其所涉及的梁格法理论均来自于Hambly的著作《Bridge Deck Behavior》中关于梁格的论述。Hambly梁格理论本身存在缺陷,没有对梁格划分方法完全分析清楚,因此没有被工程界广泛采用。Hambly的梁格法主要存在2个误区:①过分强调各纵梁截面的形心必须与原整体截面形心保持一致,因此按照 Hambly方法建立的各个纵梁一定在一个平面上,称之为平面梁格。②Hambly 梁格最初是用于分析箱梁的平面内受力,在箱梁的竖向受力分析中可以得到较真实的结果。该方法中纵梁的划分破坏了箱梁的横向剪力流路径,使得本该由箱梁顶底板传递的横向剪力流转化为各个纵梁的扭矩而施加于横梁之上。同时这种并不存在的扭矩又对横梁受力产生了干扰,使梁格模型中横梁受力失真,无法分析箱梁的剪扭问题。Hambly试图用主要关注面内受力的梁格模型来分析主要反映面外受力的箱梁剪扭效应,这种方法本身就存在天然缺陷。因此,用Hambly的平面梁格模型难以解决宽箱梁的空间受力问题。
从箱梁结构的受力特点上分析,在梁格模型中各个纵梁截面及其刚度的组合是由横梁完成的,纵梁可以自由划分,各分离截面的模型位于其本身的形心位置。按照折面梁格法建立的梁格一般不在一个平面上,故称之为折面梁格。折面梁格法在分析宽桥方面得到了广泛应用,并成为公路桥梁规范对宽桥结构计算的建议分析方法[2]。
1 工程概况
某机场的三期扩建工程需新建一条E类联络滑行道连接东西两条跑道。该联络滑行道与机场进出场路发生交叉,且在进出场路中间绿化带地下有一条明挖城际铁路箱涵,在进场路地下有一双孔地铁盾构结构。为保证机场运行安全,需设置一座滑行道桥解决飞机运行与进场路交通的相互干扰。
该滑行道桥采用了一联(21+3×30+21)m的预应力混凝土连续梁桥。上部结构采用单箱15室箱梁,梁高2.0 m,桥宽45.0 m。桥墩采用柱式花瓶墩,横桥向四墩八支座布置,桥台采用一字墙式台,基础均为桩基础。滑行道桥立面、横断面分别见图1、图2。

图1 滑行道桥立面(单位:cm)

图2 滑行道桥横断面(单位:cm)

图3 箱梁截面划分
2 计算模型
2.1 计算方法
本桥的宽跨比B/L=1.5,属于超宽桥。这种单箱多室超宽截面具有明显的剪力滞效应,且在飞机偏载作用下扭转效应突出,采用常用的单梁单元模型不能准确分析截面应力分布情况。
折面梁格法是将箱梁截面竖向划分为若干纵梁,再将各纵梁的形心连线后形成带有折面的单层梁格。此方法适用于单箱多室的宽箱梁受力分析。当将横向截面进行精细划分时,不仅无需考虑箱梁各腹板的有效分布宽度,而且能够得到顶底板横向不同位置的正应力,可以较准确反映截面正应力的横向分布[3]。
本桥上部结构折面梁格计算采用慧加结构分析与设计软件(WISEPLUS)。该软件能够解决各种异型桥梁(宽桥、弯桥、变宽桥、分叉桥、组合梁桥等)的空间问题。它具有实用精细化分析功能(7自由度梁单元分析、折面梁格分析与空间网格分析),已经成为新颁布的公路桥梁设计规范建议分析方法。该软件具有机场专用的飞机(B747-400,A380-800)荷载模块,能够进行飞机荷载的影响面分析,适用于机场飞机荷载桥梁的分析计算。
2.2 模型建立
本桥的折面梁格模型将箱梁截面划分为18个纵梁,其中1,18号纵梁为翼缘板纵梁,其余为腹板纵梁(见图3)。根据设计中的预应力钢束布置情况,将钢束分配给腹板纵梁。按照桥墩的设计位置建立支座单元,支座处的横梁按照实际横梁截面建立其模型。模型共计 2 592 个节点,4 665 个单元(见图4)。
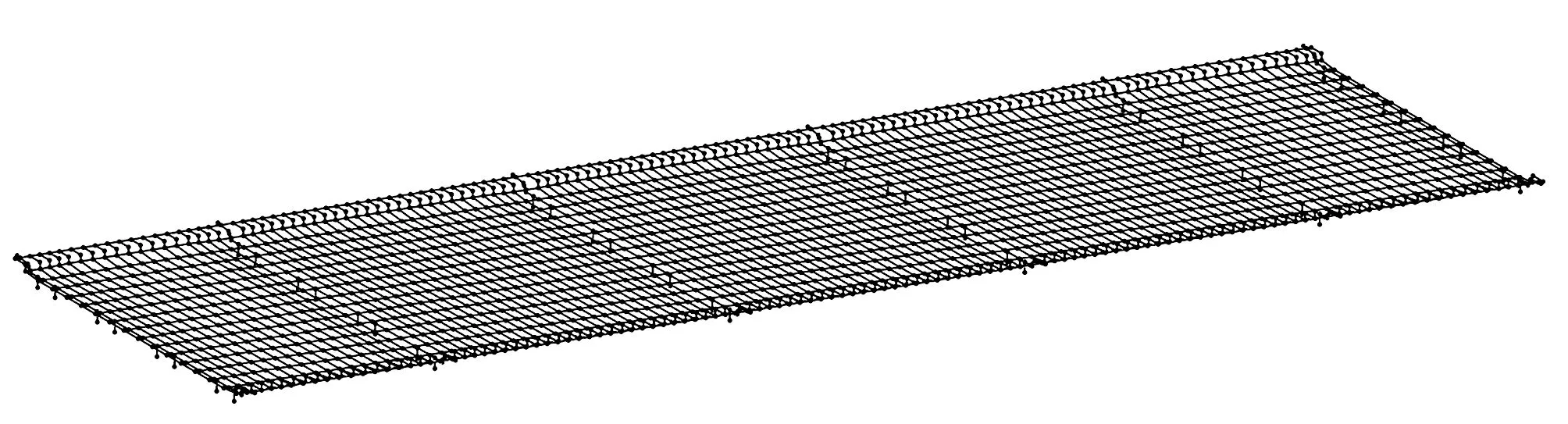
图4 全桥折面梁格模型
相关参数取值:锚具变形、钢束回缩取6 mm(一端);管道摩擦因数取0.25;管道偏差系数取 0.001 5;支座不均匀沉降取10 mm;竖向温度梯度效应按照实际桥面铺装厚度及类型考虑温度梯度的影响,按照现行规范取值;年平均相对湿度取70%;活载为E类飞机荷载(见图5)。
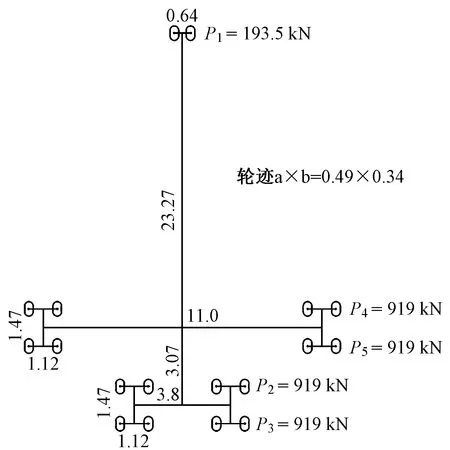
图5 飞机(B747-400)荷载(尺寸单位:m)
3 计算结果及分析
3.1 活载的空间效应
箱梁在偏载作用下将产生竖向弯曲、扭转、畸变及横向挠曲4种形态。 对于扭转、畸变、横向挠曲引起的应力,理论上应该建立箱梁横向变形协调方程进行求解,但过程相当复杂,难以应用到实际设计中。 通常根据计算效应进行设计时,传统方法通过考虑不同的内力提高系数进行设计计算,需要对不同的桥梁形式分别考虑不同的提高系数即偏载系数。一般认为,对于预应力混凝土箱形截面,由偏载引起的约束扭转正应力约为弯曲正应力的15%左右,偏载引起的剪应力约为弯曲剪应力的5%左右。基于以上的论述,在平面杆系模型计算中,计算活载正应力时偏载系数取1.15,计算活载剪应力时偏载系数取1.05。这是由于平面杆系模型无法计算箱梁扭转效应而采取的一种近似处理方法。对于承担飞机荷载的滑行道桥而言,超宽的桥面造成横向偏载较大,再采用偏载系数已经明显不能反映结构的实际受力情况[4-5]。
通过飞机荷载下梁格模型计算,得出各纵梁的空间受力情况,箱梁截面两侧的腹板正弯矩明显大于中间几个腹板。为对比方便,特列出中跨跨中2~9号纵梁正弯矩分布图(见图6)。可见,2~4号纵梁跨中弯矩明显大于5~9号纵梁,其中3号纵梁为最不利纵梁,其值为9号纵梁的1.6倍,为平均值的1.35倍。可见通常采用的弯矩偏载系数1.15对于本工程中的箱梁是偏小的。
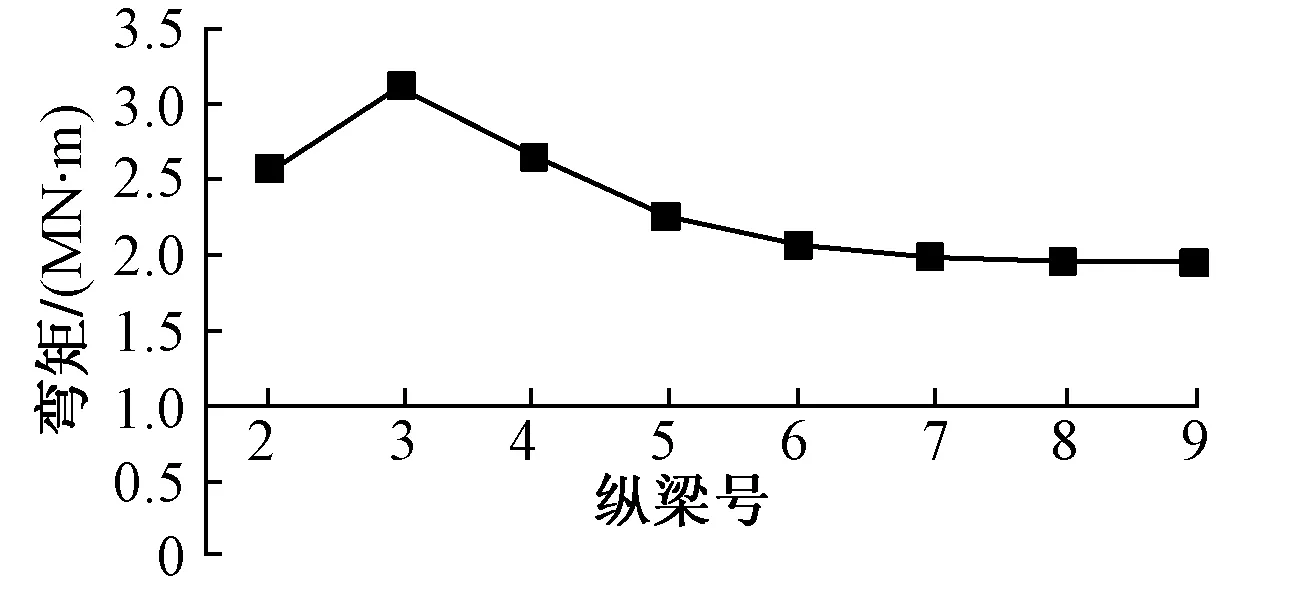
图6 飞机荷载下2~9号纵梁正弯矩分布
同样,通过分析中墩处各纵梁截面的剪力横向分布情况(见图7),也可以得出横向各纵梁的剪力分布亦不均匀,位于支座附近的3,4号纵梁剪力明显比远离支座的5,6,9号纵梁剪力大,最大值为最小值的1.66倍,为平均值的1.19倍。可见通常采用的剪力偏载系数1.05对于本工程中的箱梁也是偏小的。

图7 飞机荷载下2~9号纵梁剪力分布
通过以上分析可知,对于滑行道桥这种超宽箱梁结构且其上活载较大的情况,采用考虑活载偏载系数的分析方法与实际受力特征偏差较大,计算结果明显偏小。
3.2 剪力滞效应分析
按照初等梁理论分析箱梁竖向弯曲时,其基本假定之一是平截面假定,即不考虑剪切变形对纵向位移的影响。因此平截面假定认为箱梁翼板上的正应力沿着宽度方向是均匀分布的。实际上,尤其是宽箱梁弯曲时,远离腹板的翼缘不受弯,即受压翼缘上的压应力随着离腹板的距离增加而减小,导致纵向应力沿板宽出现不均匀分布的现象,称为剪力滞效应[6]。为研究宽箱梁截面正应力沿横桥向的分布情况,特选取梁格模型中各个纵梁(1~9号纵梁)在自重作用下墩顶处截面上下缘正应力进行分析,并与单梁模型中相同位置的截面上下缘正应力进行了对比,见图8。
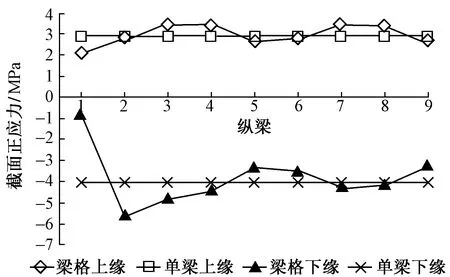
图8 墩顶处截面正应力分布
从图8中可以得出,宽箱梁截面的正应力在桥宽方向并不是均匀分布,剪力滞效应明显。折面梁格模型分析能够计算出每个纵梁的截面正应力,可以解决单梁模型计算不能考虑剪力滞的问题。
3.3 横梁计算
横梁在箱梁结构中起到连接两侧桥跨和下部结构的作用,既要承受两侧桥跨的荷载,也要承受下部结构的支反力,是非常重要的受力构件。对于超宽箱梁结构,横梁受力非常复杂,横梁的受力分析准确与否至关重要。在工程设计中,常将横梁从整体箱梁中剥离出来,简化为简支梁或者连续梁来计算。恒载按照两侧箱梁通过腹板传递给横梁的恒载考虑,将横梁所受的荷载简化为施加在各个腹板位置的集中力,活载按照车列横向布载的形式进行加载。对于只有2个腹板(即单箱单室)的箱梁,施加于横梁的集中力可以按照均布荷载考虑,但对于滑行道桥这种超宽箱梁,每道腹板实际分配给横梁多少荷载,直接影响横梁计算结果精确与否[7-10]。
对于滑行道桥而言,箱梁截面的箱室多超过10个且横向支座较多,每道腹板传递给横梁的剪力复杂多变,没有一般规律可循。单梁模型难以解决超宽箱梁各个腹板的受力问题,因此按照常规分析横梁的方法不适用于超宽且多腹板的滑行道桥箱梁。如果采用Hambly的平面梁格模型计算,虽然能够分析出超宽箱梁各个腹板的受力情况,但由于平面梁格模型本身的局限性,其模型建立时破坏了箱梁截面水平剪力的传递路径,造成横梁受力失真,与实际结构相差较大。折面梁格模型可以对纵梁、横梁作一体分析,较准确地反映横梁的受力情况,并且根据横梁内力可以直接进行设计验算。中横梁在梁格模型中的弯矩如图9所示。中横梁正常使用极限状态裂缝宽度见图10。
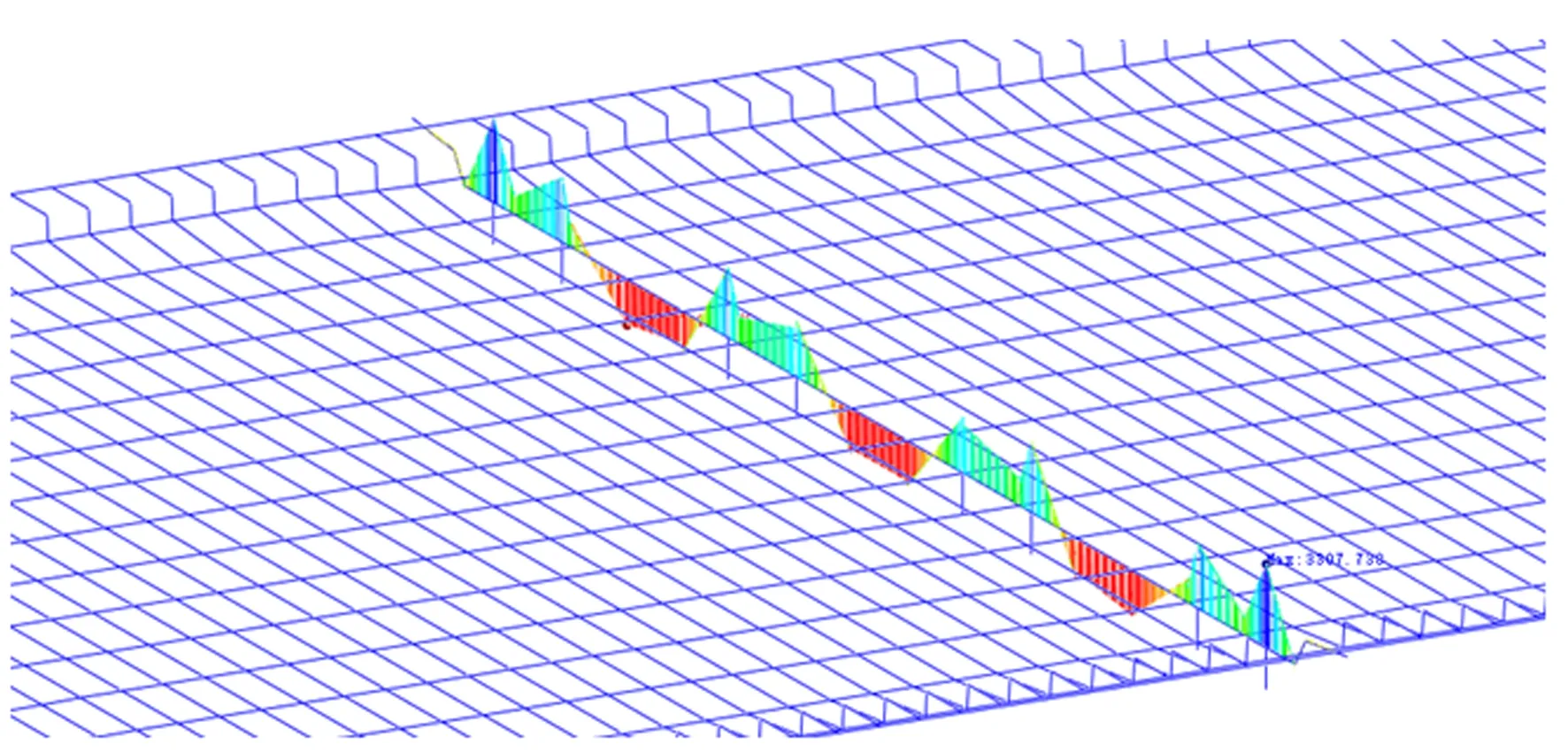
图9 中横梁在梁格模型中的弯矩
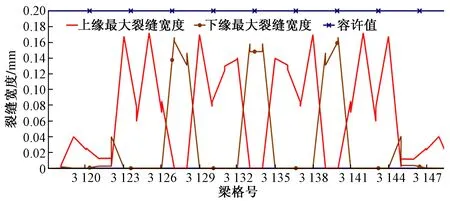
图10 中横梁正常使用极限状态裂缝宽度
4 结论与建议
1)箱梁计算中常用的偏载系数已不适用于单箱多室超宽箱梁结构,建立折面梁格模型可以准确计算各个腹板的受力情况。
2)相对于单梁模型,折面梁格模型能够较准确考虑宽箱梁截面的剪力滞效应,得出各个纵梁的正应力分布,为截面设计提供较为准确的依据。
3)常用的箱梁横梁计算方法不适用于具有多道腹板的箱梁结构,折面梁格模型可以进行纵横向整体计算,使横梁受力情况能够还原到整体结构中。
4)由于大型飞机的轮载纵横向分布复杂、荷载较大且飞机可能的滑行范围较大,常用的桥梁移动荷载影响线分析已无法反映实际情况,建议进行道面全范围的影响面分析。
