桥梁深水基础钢管桩围堰受力特性分析

陈 鹰

(中国铁建十六局集团第三工程有限公司，浙江 湖州 313000)

随着桥梁深水基础施工技术的不断发展，钢围堰在深水基础施工中得到了广泛的应用[1]。其形式包括钢板桩围堰、钢吊箱围堰、钢管桩围堰等，具有强度高、安全性能好以及施工简便、成本较低等特点[2]。目前，国内外桥墩基础施工中多采用钢板桩围堰或钢吊箱围堰形式。

现有研究成果表面，有些文献采用平面有限元对单根钢板桩进行受力分析，模拟结果与实际偏差较大，也有一些将空间有限元、平面有限元和等值梁法对桥梁深水基础钢板桩围堰受力情况进行了对比分析，结果表明采用空间有限元法能够较好地反映钢板桩围堰的实际受力情况。在深水基础施工中也常采用钢吊箱围堰、钢圆筒围堰进行桥墩的施工[3-4]，采用有限元建模对围堰结构的变形及应力分析也较为普遍。目前针对深水中桥墩施工应用钢板桩或钢圆筒围堰较多，钢管桩围堰应用相对较少。

本文以泰和赣江特大桥2#墩钢管桩围堰为依托，采用ANSYS Workbench建立空间模型，依据实际施工组织方案进行工况划分，考虑静水压力及动水压力作用，对围堰的变形及应力进行了分析。

1 工程概况

泰和赣江特大桥位于江西省吉安市泰和县，处于赣江中游地区，与已有京九线泰和赣江特大桥并行，位于其上游33 m。其中，桥梁2#墩所在区域水深11.8 m，下部为裸露基岩，下伏基岩主要为强-弱风化泥质粉砂岩，岩体完整性较好，承载力较高。

该桥址位于赣江中游地区，设计施工水位为58.8 m，常水位为56.2 m，设计流速为3.68 m/s，常水位流速为2.34 m/s。

现场施工中，2#墩围堰采用φ820 mm×10 mm锁扣钢管桩围堰，围堰顶高程为+60.8 m，施工期间水位高程为+58.8 m，下部为裸露基岩。钢管材质为Q235，单根钢管长度为18.2 m，钢管桩置于基岩顶面下3 m。为了保证围堰的整体稳定，每根钢管桩均设置钢筋混凝土锚固桩，锚固桩直径0.7 m，伸入钢管3.4 m，锚固桩总长6.5 m。钢管桩围堰平面尺寸为28.72 m×21.03 m，S1面为迎水面，S3面为背水面。围堰竖向共设置4层内支撑，4道支撑分别距钢管顶部1.5，4.5，7.5,10.0 m。锁扣钢管桩围堰内支撑腰梁采用2HW400H型钢，斜向撑杆和纵向撑杆采用φ630 mm×10 mm钢管，施工期间围堰外部主要承受静水压力和动水压力作用。在围堰外侧S1,S2面设置4个监测点，分别位于围堰外侧面4层支撑处，编号分别为S1-1，S1-2，S1-3，S1-4，S2-1，S2-2，S2-3，S2-4。见图1。

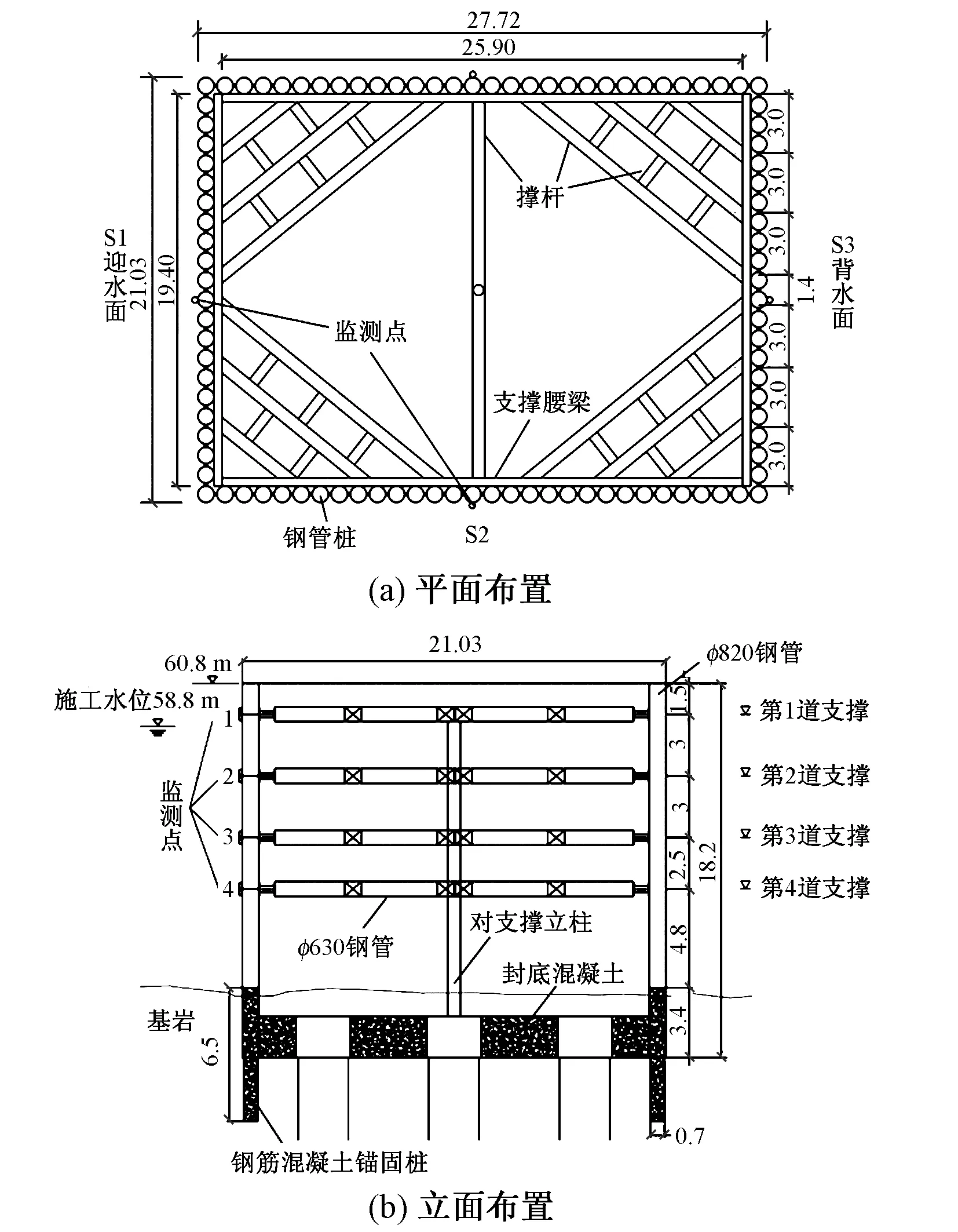
图1 钢管桩围堰布置(单位：m)

2 有限元模型计算

2.1 模型建立

参考2#围堰实际尺寸，用AutoCAD建立几何模型，导入ANSYS Workbench进行单元划分并建立有限元模型。分别施加静水压力、动水压力及自重荷载，进而根据施工工况完成施工受力分析。钢管桩围堰有限元模型如图2所示，钢管桩用空间梁单元模拟，梁截面尺寸为直径820 mm、厚度10 mm的圆形，支撑腰梁用厚度10 mm的壳单元模拟，内支撑采用相应尺寸的空间梁单元模拟。钢管桩之间连接锁扣按照等效刚度原则简化成薄板，采用厚度15 mm的壳单元进行模拟。为保证各单元之间的受力和变形协调，约束关系均采用点-面接触，不考虑相对滑移。约束顺序依次为锁扣(壳单元)-钢管桩(梁单元)-支撑腰梁(壳单元)内支撑梁(梁单元)。模型共划分单元 33 491 个，设置节点 30 110 个。

模型施加的荷载有自重荷载、静水压力及动水压力，模型底部采用固定约束，约束在钢管桩底部。围堰外静水压力呈正三角形分布，最大压力140 kPa，位于河床底部。迎水面S1所受到的动水压力呈负三角形分布，经计算最大压力为11.6 kPa，且位于水面。考虑背水面S3的波浪效应，S3受到水流的吸力作用，取值为动水压力的一半。

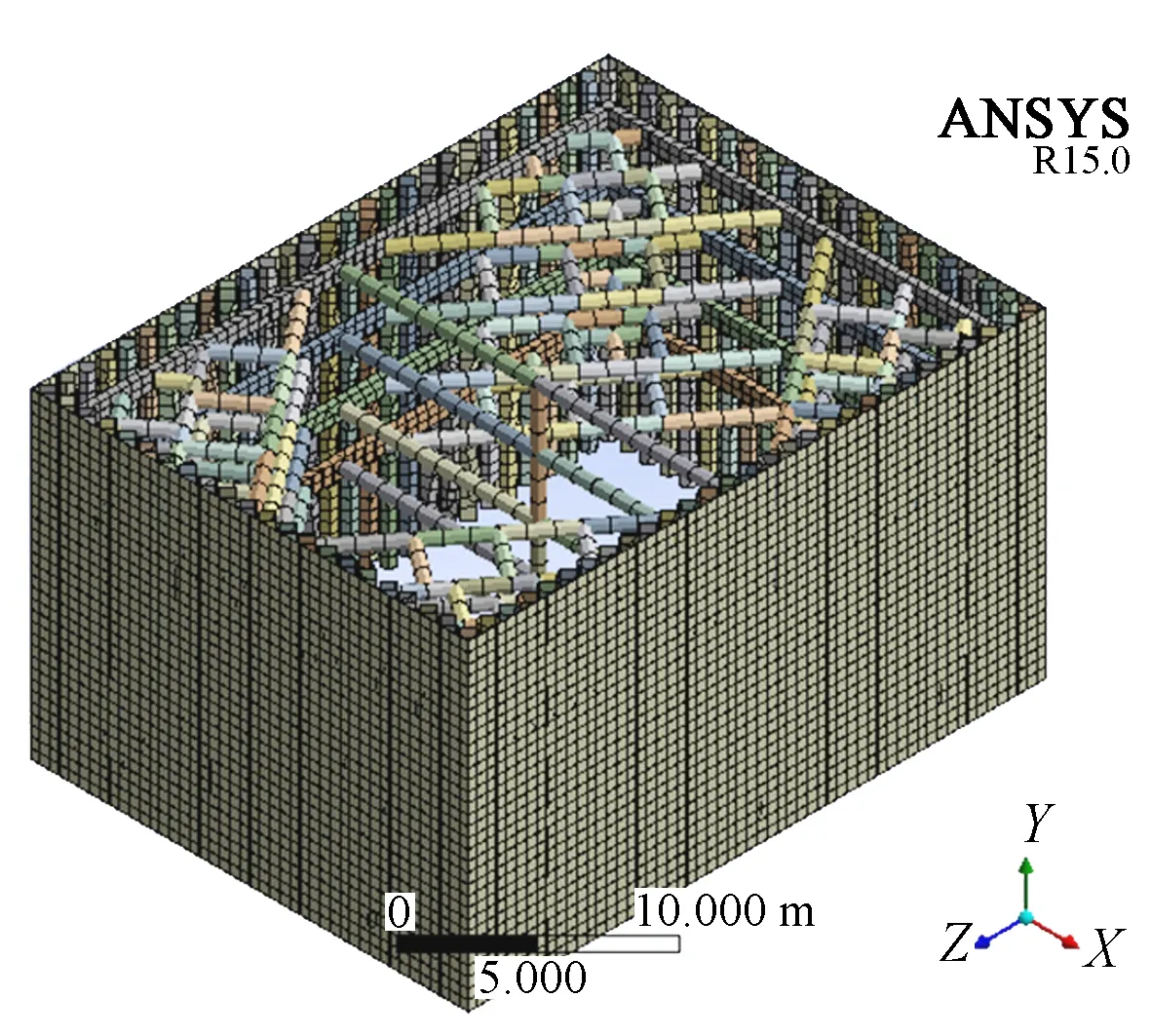
图2 钢管桩围堰有限元模型

2.2 各工况下的钢管桩围堰变形分析

桥墩的施工是一个长期过程，在施工过程中，不同工况下围堰所受到的内外压力差也不同。依据施工工序建立有限元模型，并结合工程实际，将施工过程主要划分为4个工况：①钢管桩插打完成并设置第1道支撑，围堰内抽水至第2道支撑处；②设置第2道支撑，围堰内抽水至第3道支撑处；③设置第3道支撑，围堰内抽水至第4道支撑处；④4道支撑全部设置完成，围堰内抽水至封底混凝土顶面。

根据以上4个工况，利用ANSYS有限元软件分别对各个工况下围堰受到静水压力、动水压力、重力等作用下的变形量、最大正应力和最大轴力进行计算(见表1)，从而对该围堰的稳定性进行评价。

表1 各工况下围堰变形量及受力统计

通过计算结果发现，各个工况均满足稳定条件，在工况3的时候，围堰轴向支撑压力最大为1647.9 kN，最大正应力为179.85 MPa，均满足稳定性条件。但在该工况下轴向压力较大，所受最大正应力位于围堰底部，最大值接近钢材允许值182 MPa，安全富裕较小，安全系数接近于1。故在工况3即围堰抽水至第4道支撑位置处且第4道支撑未安装的情况下，需要注意围堰底部钢管应力状况。此时第3道轴向支撑所受压力最大，在必要时需采取相应的施工措施确保施工安全。

2.2.1 变形量分析

静水压力均匀分布在钢管桩围堰四周，迎水面受到非均匀水流压力作用，迎水面与背水面承受不同的荷载。由有限元分析结果可知，钢管桩围堰的变形主要体现在横向钢圆筒支撑和钢管桩管壁的压缩变形,工况4变形云图见图3。

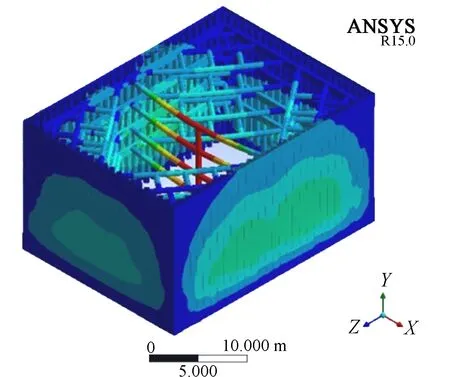
图3 工况4变形云图

数值计算结果表明，钢围堰最大变形处均为横向支撑钢圆筒处。由表1可知，设置第1道横向支撑时，内支撑钢管变形量即可达到12.53 mm，随着施工的进行，内支撑钢管的变形量逐渐增大。当设置第4道支撑且围堰内抽水至封底混凝土表面时，锁扣钢管桩围堰变形量达到最大14.74 mm；在钢管桩围堰边角处，变形量普遍较小，甚至不产生变形。钢管桩围堰的变形主要集中在抽水的初始阶段，随着抽水的不断进行，围堰的变形量增长速度不断降低，变形增量也随之减小。这是由于施工初始阶段钢管桩之间的咬合较松，当钢管桩承受初始内外压力差时，变形量较大。随着抽水的进行，钢管桩之间的锁扣咬合越来越紧密，围堰的整体刚度也得到了提高[5-8]，围堰的变形量增量也因此减小。

根据理论计算结果，在工况3和工况4条件下围堰变形量累计值最大。为保证现场施工安全，实际施工中在第2道和第3道支撑处横向设置了2根同规格的钢管，避免进入工况3和工况4的过程中产生围堰失稳现象。

2.2.2 钢管桩表面应力分析

由于监测仪器在设置第1道支撑后安装，故由监测仪器得到的应力值为围堰表面变化值。通过有限元计算，并根据现场监测点可提取相应位置处沿重力方向的应力值，得到相应的应力差值，分别为以下3种：工况2与工况1的应力差，工况3与工况1的应力差，工况4与工况1的应力差。各个工况下围堰各测点表面应力差值变化趋势如图4。

图4 围堰表面应力差值变化趋势

由图4可知，第2道横撑设置完成后，第1道支撑和第3道支撑测点处应力变化值较小，第2道和第4道支撑测点处应力变化值普遍较大，分别表现为拉应力和压应力。随着施工的进行，各个测点的应力变化情况不也同，第1道支撑与第2道支撑测点处应力变化趋势较平稳，变化值较小。当设置第3道支撑时，该处的应力呈现陡增趋势，产生了较大的变形。第4道支撑测点处应力变化值较小，当设置第4道支撑时，该处的应力也呈现陡增趋势，其他测点处应力变化趋势则较平稳。

由以上分析可知，每安装一道支撑时，该处的应力变化都较为明显，在施工过程中需要加强防范。越靠近围堰底部，钢管表面应力随施工的推进变化越明显。在第4道支撑安装处，其应力变化值最大，所受轴力也越大，在必要时需要采取相应的措施保障施工安全。

2.3 理论值与实测值对比分析

将各监测点应力差理论计算值与实测值进行对比，见图5。可以看出，随着施工的进行，在第2道支撑和第3道支撑处围堰表面的应力变化较为明显，在工况3条件下，应力变化最为显著。理论值与实测值中出现的最大应力差工况和监测位置基本一致，变化趋势也基本相同。故采用ANSYS Workbench计算可以较好地反映出围堰的应力变化情况。

由图5可知，理论值与实测值有一定的差异，最大可达到42.58%，最小只有8.55%，差值大部分在10%～30%，且实测值均小于理论值。主要原因有：在数值计算中，未考虑封底混凝土和钢管桩内混凝土的影响。由于考虑锁扣建模会加大模型计算的难度，故为简化计算，钢管桩之间连接锁扣按照等效刚度原则简化成薄板，采用厚度15 mm的壳单元进行模拟，并以理想的施工条件为前提进行模拟，故数值计算中围堰表面变形较实际偏大，相应应力变化值也较大。

3 结论

1)钢管桩围堰最大变形均在横向支撑钢圆筒处，进入工况3时变形最大，在施工初始阶段钢围堰的变形量较大。随着抽水的进行，钢管桩围堰的整体刚度提高，最大变形量增长幅值相应较小。实际施工中，在第2道和第3道横撑处分别设置了2根相同规格的钢管，避免围堰因变形较大产生失稳。

2)通过轴力和应力分析，工况3和工况4钢管柱围堰轴向支撑压力最大，且钢管桩表面最大正应力值接近钢材的允许应力值，故在必要时需采取相应的施工措施确保施工安全。

3)应用ANSYS空间有限元对围堰进行建模时，钢管桩之间的连接采用壳单元可大大减少计算量。通过将理论值与实测值进行比对表明，该建模计算结果在一定程度上可以反应出钢管桩围堰在各个工况下的受力特性。若只对单根钢管桩进行计算，定义其边界条件不太准确，故不建议采用平面有限元方法对单根钢管桩进行计算。