球谐域传播算子快速声定向算法

潘曦， 佟颖， 王华阳

(1.北京理工大学 机电学院， 北京 100081； 2.上海无线电设备研究所， 上海 200090)

0 引言

声源定向是一种应用于目标检测的被动定向方法。时间波达(TDOA)方法算法简单,是普遍使用的声源定向方法，但TDOA方法在给定的时间内只能处理单声源[1]定向问题，且定向精度和分辨率不高。多重信号分类(MUSIC)算法[2-4]和基于旋转不变技术的信号参数估计(ESPRIT)算法[5-6]是真正意义上的高分辨波达方向(DOA)方法，但不能解决宽带声源问题[7]。基于球谐波理论的球形麦克风阵列与子空间类DOA估计相结合的方法，即球谐域MUSIC (SH-MUSIC)算法能够解决宽带声源问题，并具有高定向精度[8]，主要原理是将接收信号转换到球谐域，并将球谐域的观察空间分解成噪声子空间和信号子空间，利用子空间的特性进行DOA估计。然而，该方法进行特征值分解、获取特征向量时需要很大计算量。与MUSIC算法相似，正交传播算子 (OPM)算法也是一种基于子空间的方法，但其不需要对传感器接收信号的交叉谱矩阵(CSM)进行特征值分解，并且传播算子是一个只依赖于导向向量的线性算子。因此与MUSIC算法相比，OPM算法可以显著降低计算复杂度[9]。

本文提出了基于球谐传播算子(SH-OPM)的两种声源定向算法，包括使用球傅里叶变换成分获得传播算子(SH-SFT-OPM)的算法和使用球傅里叶变换成分的CSM获得传播算子(SH-CSM-OPM)的算法。实验结果证明，与球谐域MUSIC (SH-MUSIC)算法相比，所提基于SH-OPM的算法均具有较好的声源定向性能和较低的计算复杂度。同时，为了实现对不同频带声源的DOA估计，本文分析了球阵列半径范围从0.07～0.10 m对信号频率范围从0.2～2.2 kHz的估计影响问题，总结了球阵列半径与可处理的声源频率范围之间的关系。

1 基于球麦克风阵列的声场模型

球麦克风阵列由球面上均匀分布的L个全指向声压麦克风组成，球半径为r，第l个麦克风所在方向为Ωml=(θml,φml)，在空间直角坐标系Oxyz中第l个麦克风的位置矢量表示为rml=(xml,yml,zml)T=(rsinθmlcosφml,rsinθmlsinφml,rcosθml)T，其中φ为方位角，θ为俯仰角，l=1, 2, …,L. 本文中所有方位角φ均在Omxmym面沿xm轴逆时针测得，所有俯仰角θ均沿zm轴向下测得。

假设有S个波数为k的宽带源平面波入射到阵列，其中k=2πf/c，f表示声源频率,c表示声速，且第s个平面波的波数为ks、第s个平面波的DOA为Ωs=(θs,φs)，s=1, 2, …,S. 那么第s个平面波的波矢量可被表示为ks=(kssinθscosφs,kssinθssinφs,kscosθs).

球阵列上第l个麦克风接收的声压信号的时间- 空间域模型可以写为

(1)

式中：ss(t)表示第s个声源入射信号随时间t变化的幅度；nml(t)表示麦克风接收信号中的加性噪声；τml(θs,φs)表示第s个声源入射信号到达第l个麦克风与到达球阵列球心点处的时间差，

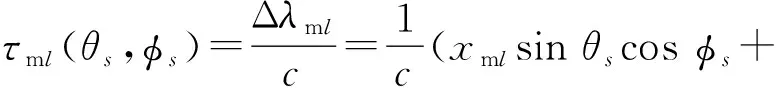
(2)

Δλml为第l个麦克风所在位置与球阵列球心点处在入射方向(θs,φs)上的波程差。

对(1)式进行傅里叶变换，得到频率- 空间域模型：

(3)

将(2)式中的τml(θs,φs)代入(3)式，得

(4)

将(4)式写为矩阵形式：

(5)

记作

P(k)=A(k)s(k)+n(k)，

(6)

式中：A(k)∈CL×S表示导向矩阵, 可写为

(7)

s(k)∈CS×1且s(k)=[s1(k),s2(k),…，sS(k)]T表示信号波形向量；n(k)∈CL×1且n(k)=[n1(k),n2(k),…，nL(k)]T表示和信号向量s(k)无关的加性噪声向量。

与窄带声源信号不同，对于宽带声源信号的导向矩阵A(k)，其频率f表示整个信号频带，这里自变量波数k=2πf/c不是固定值，而是整个频带对应的不同波数。通过对接收信号进行离散采样获得数字信号，然后选取X个快拍进行X点离散傅里叶变换，就会得到X个离散的频率点，相当于将宽带声源信号的整个频带分成X个子频带，每个子频带对应的频率为fx(x=1, 2, …,X)，相应的波数为kx=2πfx/c. 那么(6)式离散化为

P(kx)=A(kx)s(kx)+n(kx).

(8)

对于单位幅度的平面波入射声场球谐函数展开式可写为

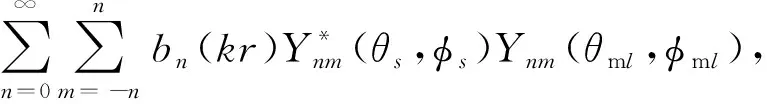
(9)

式中：k为波矢量；r为麦克风的位置矢量；Ynm(θ,φ)表示n阶m维度的球谐函数，且

(10)

Pnm(cosθ)表示缔合勒让德函数；bn(kr)称为模态强度，且有

(11)

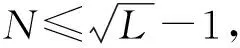
(12)

将(12)式代入(7)式中，导向矩阵A(k)可被分解为

A(k)=Y(ΩmL)B(kr)YH(ΩS).

(13)

式中：Y(ΩmL)∈CL×(N+1)2为球谐函数矩阵，

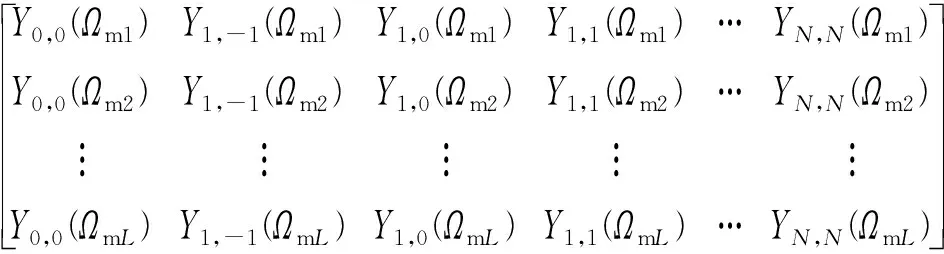
(14)

B(kr)为远场模态强度的对角矩阵，

B(kr)=diag(b0(kr),b1(kr),b1(kr),…,bN(kr))；

(15)

Y(ΩS)∈CS×(N+1)2为入射声源的球谐波矩阵，

(16)

将(13)式代入(8)式，得

P(k)=Y(ΩmL)B(kr)YH(ΩS)s(k)+n(k).

(17)

(17)式即为声场球谐函数展开的矩阵表达式，给(17)式左右两边同时乘以YH(ΩmL)×V，其中V∈CL×L表示权重因子的对角矩阵，

V=diag(αm1,αm2,…,αml,…,αmL)，

(18)

式中：αml=4π/l，其中l=1,2,…,L表示整个采样点集。

对声场进行球谐分解，可得球傅里叶系数矩阵为

Pnm(k)=B(kr)YH(ΩmL)s(k)+nnm(k)，

(19)

式中：nnm(k)=YH(ΩmL)×V×n(k)为加性噪声球傅里叶变换系数矩阵。注意到(19)式中球傅里叶系数向量的导向向量为B(kr)YH(ΩmL)，即频率相关的分量已从角度相关的分量中解耦出来。这时通过给(19)式左乘B-1(kr)即可将频率相关的分量去除，获得只包含角度相关的分量，即球傅里叶变换成分Pnm∈C(N+1)2×1写为

Pnm(k)=YH(ΩS)s(kx)+N(kx)，

(20)

式中：N(kx)∈C(N+1)2×1，且N(kx)=B-1(kr)×YH(ΩmL)×V×n(kx)。定义矩阵F(kx)∈C(N+1)2×L，令

F(kx)=B-1(kr)×YH(ΩmL)×V，

(21)

则N(kx)可被重写为

N(kx)=F(kx)×n(kx).

(22)

2 球谐域的传播算子定向算法

2.1 SH-SFT-OPM算法

对于宽带声源，其频率覆盖范围宽。波数k=2πf/c的范围由声信号的带宽决定，现将声信号分解成X个子频带，则球傅里叶变换成分Pnm(k)宽带信号的球傅里叶变换成分Pnm∈C(N+1)2×X可被写为

Pnm=[Pnm(k1),Pnm(k2),…,Pnm(kX)].

(23)

传播算子的定义基于对球傅里叶变换成分Pnm获得

Pnm=[PA;PB],

(24)

式中：PA∈CS×X表示由矩阵Pnm的前S行组成的子矩阵；PB∈CU×X表示由矩阵Pnm的后U行组成的子矩阵，U=(N+1)2-S.

假定所有的入射信号均不相干，则矩阵Pnm满秩保证了子矩阵PA的行线性独立。

在无噪声的情况下，存在着矩阵P使得(25)式成立：

PB=PHPA.

(25)

当存在噪声时，尽管(24)式仍然成立，(25)式关系已不再满足。这时传播算子SFT估计值可以通过最小二乘法获得，可表示为

(26)

QHa(Ωs)=0，

(27)

于是DOA估计函数为

FPM(Ωs)=aH(Ωs)QQHa(Ωs).

(28)

为了引入噪声空间的投影算子，可以用其正交化矩阵取代矩阵Q，即

Q0=Q(QHQ)-1/2，

(29)

则DOA估计的伪谱为

(30)

通过扫描入射声源方向Ω, 伪谱中最大的峰值对应的Ω即为声源的入射方向Ωs.

2.2 SH-CSM-OPM算法

X个子频带的CSMRnm∈C(N+1)2×(N+1)2可被写为

(31)

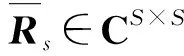
(32)

(33)

(34)

(35)

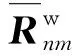
在无噪声的情况下，存在着矩阵P使得(36)式成立：

H=GP.

(36)

当存在噪声时，尽管(24)式和(35)式的分块仍然成立，但(25)式和(36)式的关系已不再满足。这时传播算子CSM的估计值可以通过最小二乘法获得，可表示为

CSM=(GHG)-1GHH.

(37)

获取传播算子后，构建矩阵Q以及DOA估计都与SH-STF-OPM算法相同。

3 仿真及性能分析

在基于球形麦克风阵列的DOA估计中，DOA的估计性能主要取决于球傅里叶变换成分Pnm的准确性。本节通过定义球傅里叶变换成分的信噪比(SNR-SFT)对球麦克风阵列的DOA估计性能进行分析。

3.1 球阵列半径与可处理的声源频率范围

为了考虑不同来源的误差，通过随机过程仿真球形麦克风阵列的性能。给定L个麦克风以一个给定的安装误差均匀地分布在球形阵列的表面。用球阵列上L个麦克风接收到的声压信号计算S个平面波的来波方向[12]，且所有的接收声压值都添加了随机噪声。使用球形阵列的SNR-SFT可写为

(38)

式中：‖·‖F表示Frobenius范数；nm(k)表示球傅里叶变换成分的估计值。Pnm(k)和nm(k)可分别写为

Pnm(k)=YH(Ωs)s(k)，

(39)

nm(k)=F(k)A(k)s(k)+F(k)n(k).

(40)

结合图1和图2可以得出：在低频处球傅里叶变换成分的估计值nm并不真正等于其理论值Pnm，这种现象控制了球麦克风阵列可处理频率范围的下边界；在高频处由于空间混叠的存在，限制了球麦克风阵列的性能[13]。对半径和阵列可处理的频率范围作了相应的分析，结果如图3所示。从图3中可以看出，随着球阵列半径的增加，阵列DOA估计可处理的声源信号频率范围先增加、后下降。

3.2 传播算法DOA估计性能

本节所有的仿真均使用同一个远场正弦线性扫频信号，该信号频率范围为0.2～2.2 kHz，并以8 kHz/s频率变化率线性扫频。声信号的入射方向(θ,φ)为(100°, 100°)。麦克风接收信号的信噪比设置为0 dB. 快拍数为512个，采样率为10.24 kHz.

使用半径为0.07 m刚性单球阵列，进行仿真实验，图4给出了3种DOA估计算法的空间谱。通过比较可以得出：图4(a)中使用SH-SFT-OPM 算法的DOA估计准确性最差；图4(b)和图4(c)中分别使用SH-CSM-OPM算法和SH-MUSIC算法的DOA估计结果非常接近，和图4(a)中使用SH-SFT-OPM 算法得到的空间谱相比，这两种算法的空间谱谱峰均很尖锐。

通过比较3种算法DOA估计结果的均方根误差(RMSE)分析这3种算法在不同信噪比下的DOA估计性能。RMSE由 (41)式计算：

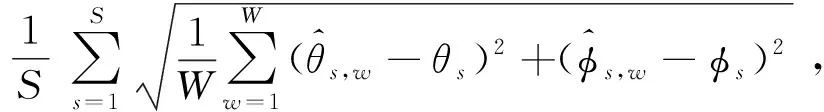
(41)

式中：S和W分别表示声源个数和独立的蒙特卡洛实验次数；(s,w,s,w)表示第w次蒙特卡洛实验中以(θs,φs)方向入射到阵列第s个声源的DOA估计值[14]。俯仰角和方位角的扫描间隔设为(1°, 1°)，麦克风接收信号的信噪比为-10～20 dB. 入射声源信号的所有参数即3.2节开头所设。使用半径为0.07 m的刚性单球阵列对SH-SFT-OPM算法、SH-CSM-OPM算法和SH-MUSIC算法3种DOA估计算法进行估计误差分析，共进行500次独立蒙特卡洛实验，得到RMSE随信噪比(SNR)变化的结果如图5所示。

从图5可知：本文所提SH-SFT-OPM算法和SH-CSM-OPM 算法在信噪比为0～20 dB时具有与SH-MUSIC算法相似的性能；在信噪比低于0 dB时所提算法的RMSE比SH-MUSIC算法小，特别是SH-SFT-OPM算法不需要计算CSM，也不需要进行白化，因此该算法具有最低的计算复杂度，在对实时性要求较高的环境中具有实际应用价值。

4 实验及测试结果分析

4.1 球阵列设计

为了验证本文所提基于球形阵列宽带源快速定向算法的有效性，本节设计了表面均匀分布8个全指向麦克风的球形阵列结构[14]，球阵列半径为0.07 m，8个麦克风被安装在刚性球内接正方体的8个顶点上，刚性球阵列实物图如图6所示，8个麦克风所在方位如表1所示。

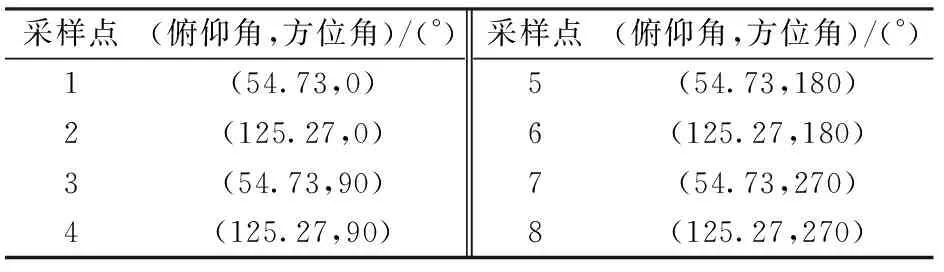
表1 球阵列表面8个麦克风所在方位

4.2 定位误差分析

将声源固定在不同的方位进行声源定向实验，所用声源信号为录制的坦克行走声音，该声信号的某段时域波形如图7所示，同时图8给出了对应的声源信号幅频图。图8中结果显示所用声源频率范围主要集中在200～1 500 Hz之间。

图9为实际声源方向测量实验场景，用蓝牙音箱分别在距离球阵列中心2 m处8个不同的空间位置播放声音，图10给出了8个声源空间位置的示意图，图中灰色小球表示球阵列，赤道圆环上的4个黑色小点表示实验位置1到实验位置4中俯仰角固定为90°时方位角分别为0°、90°、180°、270°的位置，4个蓝色小点表示实验位置5到实验位置8中固定方位角为180°时，俯仰角分别为30°、60°、120°、150°的位置。

每个声源位置都进行了100次独立实验，并使用3种不同算法进行计算，所得结果的平均值如表2所示，使用SH-CSM-OPM算法进行第3次测量结果的空间谱三维图和俯视图分别如图11(a)和图11(b)所示。

表2 8个不同空间位置测得的声源方向平均值

从表2中可以看出，所提算法能够准确识别声源DOA. 其中SH-SFT-OPM算法估计精度较差，最大估计误差为(4°, 6°)；而SH-CSM-OPM算法和SH-MUSIC算法估计结果相近，最大估计误差为(3°, 5°)。综上所述，实验结果证明了所提算法的有效性。

4.3 时间开销

测试了使用该单球阵列进行SH-SFT-OPM算法、SH-CSM-OPM算法和SH-MUSIC算法3种DOA估计算法花费的时间。表3给出了经过10次实验的平均花费时间。

表3 10次实验的平均花费时间

由表3可以看出，随着扫描间隔的变小，3种算法DOA估计花费的时间快速地增大，其中SH-SFT-OPM算法花费的时间更少，这是因为该算法不需要计算CSM，也不需要噪声白化。而SH-CSM-OPM算法和SH-MUSIC算法花费的时间非常相近。

5 结论

本文提出了基于SH-OPM的两种声源定向算法：SH-SFT-OPM算法和SH-CSM-OPM算法。总结了球阵列半径与可处理的声源频率范围之间的关系，解决了宽带声源频率适应性问题。通过比较分析两种算法和SH-MUSIC算法在不同信噪比下的DOA估计性能，进行声源定向实验并测试了3种算法的DOA估计用时，得到了如下结论：

1)所提算法在信噪比为0～20 dB时具有和SH-MUSIC算法相似的性能；在信噪比低于0 dB时所提算法的RMSE比SH-MUSIC算法小，特别地，SH-SFT-OPM算法具有最低的计算复杂度，在对实时性要求较高的环境中具有实际应用价值。

2)所提算法能够准确识别声源波达方向。其中SH-SFT-OPM算法估计精度较差，SH-CSM-OPM算法和SH-MUSIC算法估计结果相近。

3)随着扫描间隔的变小，3种算法DOA估计花费的时间快速增大。其中SH-SFT-OPM算法花费的时间更少，这是因为该算法不需要计算CSM以及噪声白化，而SH-CSM-OPM 算法和SH-MUSIC算法花费的时间相近。