光电稳定平台伺服机构低速及稳定性能控制方法研究

2018-11-07祁超范世珣谢馨陈宁范大鹏江献良

兵工学报 2018年10期

祁超，范世珣，谢馨，陈宁，范大鹏，江献良

(国防科技大学智能科学学院，湖南长沙 410073)

0 引言

光电稳定平台广泛应用于车载、机载武器系统中[1-3]，光电伺服机构是其实现高性能稳定的关键部件，基本组成包括转轴电机、传动部件、光电载荷、功率放大模块、运动控制模块以及测角/测速传感器。根据负载及工作环境的不同，光电伺服机构的传动部件采用多种形式，其中以电机直驱、谐波传动以及摆线针轮行星(RV)传动3种类型最为常见。

低速平稳性和稳定精度是评价光电伺服机构性能的两项核心技术指标。其中，低速平稳性用于衡量光电稳定平台对远距离运动目标的持续跟踪能力，在高性能应用场合，通常要求平稳运动速度优于0.01°/s；稳定精度用于衡量光电探测器视轴在惯性空间中的稳定性能，通常要求视轴的稳定精度优于0.2 mrad. 低速平稳性及稳定精度均与电机堵转力矩、传动件和框架柔性、结构装配精度、传感器信号质量以及运动控制算法密切相关[4]。由于影响因素较多，非线性特征明显，低速平稳性和稳定精度始终是光电伺服机构性能优化的重点和难点。

在工程应用方面，光电伺服机构当前采用的控制方法仍以经典控制为主。经典控制方法的实现过程相对简单，对于大多数伺服性能要求不高的场合能够获得满意的性能。但经典控制方法本质上属于线性控制，对于转矩扰动等非线性因素无法进行有效抑制，因此在光电稳定平台等要求高性能运动的应用场合，使用经典控制方法往往无法获得理想性能。而在理论研究方面，研究人员提出了很多用于提升伺服机构低速平稳性及稳定精度的先进控制策略，然而部分算法结构过于复杂、计算量很大，导致实现困难，且实时性问题难以解决。还有部分算法仅在个别机构中进行了验证，缺乏在不同类型伺服机构上进行实验测试的结论，因此对其有效性的检验尚不充分。

针对经典控制算法难以抑制转矩扰动，同时先进控制算法在实时性及有效性方面无法得到保证的问题，本文将传统比例积分(PI)控制算法、状态扩展Kalman滤波(SAKF)算法和前馈控制算法相结合，提出一种基于SAKF的捷联稳定控制算法。该算法采用SAKF观测扰动转矩和电机转速，采用前馈控制器来提升系统响应速度，采用反馈控制器来修正控制误差。本文给出了规范化的算法实现步骤，并对控制算法参数的设置进行详细说明，使得算法更具有可实现性。最后，在电机直驱、谐波传动以及RV传动3类伺服机构上开展控制性能对比实验，充分验证了控制算法的有效性。

1 光电伺服机构动力学模型

光电伺服机构的稳定精度与低速平稳性取决于其单轴伺服机构运动性能。高性能的运动控制器通常需要基于准确的动力学模型进行设计，因此，本节对单轴伺服机构动力学模型的设计过程进行重点说明，并基于该模型分析经典控制方法的局限性，从而为设计单轴伺服机构的高性能控制算法奠定基础。

1.1 单轴伺服机构动力学模型

单轴伺服机构动力学方程组[5]为

(1)

式中：Kt为电机转矩系数；i为电机电流；J为电机端等效转动惯量；ωm为电机转速；um为电机电压；Lm为电枢电感；R为电枢电阻；Ke为反向电动势系数；Mf为摩擦转矩；Tc为库伦摩擦转矩；B为黏滞摩擦系数；Kc为电流环控制器增益；Kg为功率放大器增益；u为电流环输入电压；Ka为电流环反馈系数；v为负载端转速；Kr为传动比；θ为负载端角位置。

根据(1)式可以构建图1(a)所示的速度开环传递函数模型，其传递函数可以表示为

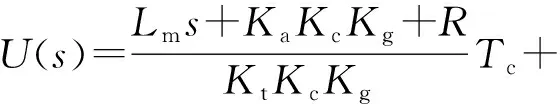
(2)

式中：V(s)为负载端转速v的拉式变换；s为拉普拉斯算子。

为实现对转矩扰动的观测，对模型(2)式进行适当化简。考虑到电流环带宽截止频率远大于系统工作频率，因此可以将模型的电流环部分等效为比例环节，并进一步将库伦摩擦转矩Tc折算到指令端，得到图1(b)所示速度开环简化模型，其传递函数为

(3)

(4)

1.2 经典控制方法的局限性分析

经典控制方法通常以线性模型(4)式设计速度闭环反馈控制器。设控制器传递函数为C(s)，指令为Vr，则有

U(s)=C(s)(Vr-V(s)).

(5)

将(5)式代入(4)式，并消去U(s)，可得

(6)

然而由于实际系统中存在以库伦摩擦为主要组成的转矩扰动，这些扰动因素可以等效为电压d作用于电流环输入端，如图1(b)所示。设D(s)为等效电压d的拉氏变换，则只需将(4)式中的U(s)替换为U(s)-D(s)，再由(5)式可得

(7)

2 控制算法设计

控制算法的设计围绕伺服机构低速平稳性和稳定精度提升的主题展开，因此在进行控制器设计之前，有必要明确上述性能指标的定义与测量标准。本节首先给出伺服机构低速平稳性与稳定精度的常规定义及量化方法，然后对控制算法的结构组成进行分析，并针对算法的各组成环节，依次介绍设计思路。

2.1 性能指标定义

为保证性能指标评价的标准性和通用性，对低速平稳性和稳定精度均参考国家军用标准进行定义。

2.1.1 低速平稳性

国家军用标准GJB1801—93惯性技术测试设备主要性能试验方法给出了低速平稳性的评价方法[7]。设平台的初始角位置为θ0，当系统以速度ω运动时，理想运动轨迹为θ0+ωt，然后用相对理想运动轨迹偏移量为±Δθ的两条平行线θ0+ωt+Δθ和θ0+ωt-Δθ包络系统的运动轨迹曲线，如图2所示。当运动轨迹曲线几乎全部(95%)被包络在平行线之间时，则认为系统以速度ω运动的平稳性为Δθ. 显然，Δθ越小，以速度ω运动的平稳性越好。

2.1.2 稳定精度

伺服机构稳定精度的定义方式通常有两种[8-9]：一种是当载体作幅值为A、频率为f的正弦摆动时，取被控对象实际角度与理想角度的误差幅值e作为稳定精度(mrad)；另一种是取误差幅值e与载体摆动幅值A的比值作为稳定精度，其单位为1，通常以百分数表示，称为隔离度[8]。显然，当给定载体扰动时，稳定精度的上述两种定义方式能够相互转换。因此，如不作特别说明，后文将统一采用隔离度作为伺服机构稳定精度的定义方式。

2.2 控制算法结构

本文提出的控制算法构成如图3所示，其输入为伺服机构在惯性空间中的稳定转速指令ωr，输出为伺服机构实际稳定速度ω. 图3中SAKF根据伺服机构的输入电压u及输出转速v进行转矩扰动d的观测及补偿；与此同时，该模块还对伺服机构的转速v进行滤波，得到具有更高信噪比的速度估计信号，用于反馈控制；Cv(s)模块为反馈控制器，采用经典控制方法实现；F(s)模块为前馈控制器，用于补偿动态误差，以进一步提升系统带宽。上述控制模块一并构成了速度跟踪单元，如图3虚线框中所示。如果SAKF模块对转速v的观测足够准确，并且速度跟踪单元具有足够带宽，则对于低频速度指令vr，必有vr==v. 在此基础上，将陀螺安装于载体上，其敏感轴与载体转轴平行，用于感知载体扰动(即捷联稳定方式)。设载体在惯性空间的转速为ωd，陀螺测速信号为ωg，由于陀螺带宽远高于载体扰动带宽，ωd=ωg. 将指令ωr与ωg相减作为速度跟踪单元输入指令vr，于是ωr-ωg=vr==v=ω-ωd=ω-ωg，因此有ωr=ω，从而实现了伺服机构在惯性空间指向稳定。图3中，uF为前馈控制量输出，uC为反馈控制量输出。

2.3 控制算法功能单元的设计

通过对控制算法的结构分析可知，SAKF、前馈控制器以及反馈控制器为算法的3个功能单元，下面对这3个单元的设计过程予以详细说明。

2.3.1 SAKF设计

SAKF基于系统状态空间方程设计，为此将传递函数模型Guv转化为对应的状态空间方程：

(8)

为实现对扰动d的观测和补偿，需要将扰动并入状态向量中，此即所谓“状态扩展”的含义。为此，对(8)式进行离散化，离散过程考虑扰动d变化连续的实际情况，认为对扰动的相邻采样值之差为白噪声ωn，即d(k+1)=d(k)+ωn(k)；同时考虑模型状态误差n(k)和传感器量测噪声nm(k)的影响，在离散状态空间方程中分别引入相应噪声项。据此获得状态变量为角位置θ(k)、角速度v(k)以及扰动d(k)的离散状态扩展空间方程：

(9)

根据(8)式和(9)式，可知Ad、Bd与p、K之间存在(10)式所示函数关系：

(10)

基于SAKF进行状态变量估计的原理如图4所示，图中L为Kalman滤波增益矩阵，状态变量的估计结果可以表示为

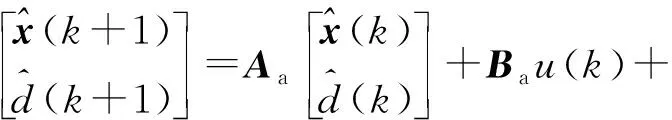
(11)

由此可知，SAKF设计的关键在于确定滤波增益矩阵L. 为此，可根据离散扩展状态空间方程(9)式，结合系统外部扰动、控制信号及观测信号的分辨率和信噪比，通过(12)式求解得到滤波增益矩阵：

(12)

式中：M为稳态估计协方差矩阵，该参数可通过求解离散黎卡提方程(13)式得到：

(13)

Rw为输入信号的噪声协方差矩阵；Rr为量测信号及扰动信号的噪声协方差矩阵。

2.3.2 前馈控制器设计

(14)

式中：fQ为低通滤波器的截止频率(Hz)；ξF为滤波器阻尼系数，通常取0.707.

对(14)式进行离散化，并设离散周期为Ts，输入指令为vr，输出为uF，则有

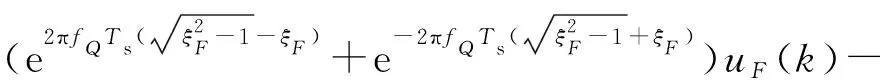
(15)

2.3.3 反馈控制器设计

反馈控制器的设计考虑采用经典控制方法。为保证系统工作稳定，反馈控制器的阶次不宜过高，因此通常采用PI控制器，其表达式为

(16)

式中：KP、KI分别为PI控制器的比例环节增益和积分环节增益。

反馈控制器的输入来自速度指令vr与速度观测值之差，设控制器输出为uC，由(16)式可得

uC(k+1)=uC(k)+KP(vr(k+1)-(k+1))+
KITs(vr(k)-(k)).

(17)

3 控制算法实现

由于控制算法的3个功能单元相互关联，在实现时具有严格的逻辑顺序；同时，算法参数的合理设置对于获取良好的伺服性能至关重要。为此，本节从算法实现步骤及参数设置两个方面介绍控制算法的实现。

3.1 算法实现步骤

控制算法的实现步骤如下：

1) 控制算法初值设置。首先通过实验辨识，得到系统1阶传递函数极点p和增益K；然后根据(9)式～(13)式，求出滤波增益矩阵L=[L1,L2,L3]T，并取状态观测量(0)=0、(0)=0、(0)=0，以此作为SAKF算法的运算初值；再取uF(0)=0、uC(0)=0，分别作为前馈控制器和反馈控制器的计算初值。

2)速度观测量及转矩扰动补偿量计算。将(9)式和(10)式代入(11)式中，可得速度观测量(k)及转矩扰动补偿量(k)的递推表达式：

(k+1)=(k)+L3(v(k)-(k))，

(18)

(k+1)=(e-pTs-L2)(k)+L2v(k)-

(19)

3) 前馈控制量计算。计算(15)式，获得前馈控制量uF(k)的递推计算结果。

4) 反馈控制量计算。计算(17)式，得到反馈控制量uC(k)的递推计算结果。

5) 控制量输出求和。将反馈控制量、前馈控制量以及SAKF、转矩扰动补偿量求和，得到完整的控制量：

u(k)=(k)+uF(k)+uC(k).

(20)

6) 系统状态变量更新。在完成控制量u(k)的第1次解算后，按(21)式对状态观测量(k)、(k)、(k)及控制量uF(k)、uC(k)进行更新，后续每一次迭代计算均按照步骤2～步骤6的顺序循环进行。

(21)

3.2 算法参数设置

控制算法的3个功能单元中：SAKF中待整定参数为模型误差协方差Rw和量测噪声协方差Rr；反馈回路采用PI控制器，其待整定参数为增益KP和积分环节系数KI；前馈控制器中需要调节的参数为低通滤波器截止频率fF，合理配置控制器参数对于提升光电伺服机构性能至关重要，为此本节分别就上述控制算法参数的设置进行说明。

3.2.1 SAKF参数设置

根据(9)式可知，SAKF的模型误差协方差Rw=diag[σθ,σv,σd]，量测噪声协方差Rr=diag[σθ,σv]，为获得Rw和Rr，需分别确定其对角线元素参数σθ、σv、σd.

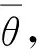
对于Rw，由于所建立的动力学模型与实际被控对象之间存在一定偏差，需结合实测曲线与模型的拟合程度，以及实际扰动信号的信噪比等来确定具体参数，通常需要手动调参。

3.2.2 反馈控制器参数设置

反馈控制器采用PI控制，在SAKF参数配置合理的情况下，能够获得具有更高质量的速度反馈信号，并且可以有效补偿系统中的非线性扰动。因此可以认为经扰动补偿后的系统动力学特性接近于理想线性模型(4)式，所以对反馈控制器参数的整定可以基于理想线性模型(4)式进行。

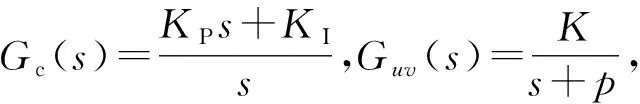
(22)

令|Go(jω)|=1，可得KP、KI与截止频率ωc存在关系：

(23)

此时开环相角

(24)

因此相角裕度

(25)

(26)

设被控对象的谐振频率为fR，在谐振频率处的阻尼系数为ξR，则有闭环带宽fB≤2fRξR. 通常ξR∈(0.1,0.35)，取ξR=0.25，则

fB≤0.5fR.

(27)

系统的闭环带宽fB和开环截止频率fC之间存在关系式：

fB=2fC.

(28)

因此可以得到开环截止频率fC与谐振频率fR的关系[3]：

fC≤0.25fR.

(29)

取fC=0.25fR，并结合(26)式，可以建立起PI控制器增益KP、积分环节增益KI与谐振频率fR的关系：

(30)

因此，在确定被控对象的谐振频率fR和相角裕度θ后，即可根据(30)式获得满足条件的PI控制器参数。

3.2.3 前馈控制器参数设置

带前馈通道的系统传递函数可以表示为

(31)

因此相角φ=arg (Q+GcGuv)-arg (1+GcGuv).

结合(4)式和(14)式，可得

(32)

对(32)式可知，φ(f)在低频段取值很小，表明低频段几乎没有滞后。因此，要使被控对象在带宽范围内具有良好的跟踪性能，可令谐振频率fR处的响应相对激励超前相角φm，即φ(fR)=φm，容易解出：

(33)

因此给定相角φm，即可根据(33)式得到前馈滤波截止频率fQ.

4 控制性能实验

为验证控制算法对不同伺服机构性能提升的有效性，以电机直驱部件、谐波传动部件以及RV传动部件为研究对象，围绕低速平稳性和稳定精度两个核心指标，开展传统PI控制算法与PI+SAKF+前馈控制算法的对比检验。

4.1 实验平台简介

实验平台的主体部分由摇摆台、传动部件、陀螺、dSPACE半实物仿真平台和供电设备组成。其中，摇摆台用于模拟载体的扰动，可由PC机设置摆动的幅值及频率；陀螺安装在摇摆台上，其敏感方向与摇摆台的转轴平行，用于感知摇摆台在惯性空间中的转速，从而实现传动部件的捷联稳定；dSPACE平台用于对控制算法进行设计与验证；供电设备则用于为实验平台的各个单元提供功率输入。实验平台的实物图及组成框图分别如图5和图6所示，其主要组成部件的型号及参数参见表1.

4.2 实验结果对比

4.2.1 低速平稳性能对比

以PI控制算法与本文提出的PI+SAKF+前馈控制算法，分别对直驱部件、谐波传动部件和RV传动部件3个部件进行速度闭环控制。保持摇摆台静止，将速度指令设置为0.01°/s进行多组实验，采集每组实验的编码器角位置数据，并绘制出角位置与时间的关系曲线，典型曲线如图7所示，其中红色斜线表示采用PI控制算法时的运动轨迹包络线；蓝色斜线表示采用PI+SAKF+前馈控制算法时的运动

表1 实验设备的主要参数

轨迹包络线。

采用2.1.1节提供的低速运动平稳性量化方法，对图7曲线的波动幅值进行测量，分别得到两种控制方式下的低速运动平稳性量化结果，如表2所示。

表2 低速平稳性能对比

分析表2数据可知，与采用PI控制算法相比，采用本文提出的PI+SAKF+前馈控制算法时，3个部件的低速平稳性量化数值更小，表明采用本文控制算法能够得到更好的低速运动性能。

4.2.2 稳定精度性能对比

将摇摆台设置为运动幅值1°、频率1 Hz的正弦摆动，并使伺服机构处于陀螺闭环，采用PI控制算法和本文的PI+SAKF+前馈控制算法分别对3个部件进行稳定精度测试。取空间转速指令为0，待系统处于稳态后，将摇摆台角度与伺服机构角度做差，即可得到伺服机构相对于惯性空间的残余运动波形。由于摇摆台的运动幅值为1°，残余运动的幅值在数值上等于隔离度。

对每个部件进行多组稳定精度对比实验，其残余运动的典型曲线如图8所示，为了直观显示伺服机构稳定效果，将摇摆台所模拟的载体扰动角度也表示在图8中。

基于2.1.2节中隔离度的定义，得出两种控制算法对伺服机构的稳定精度对比结果，如表3所示。从表3中数据可见，在相同的载体扰动条件下， PI+SAKF+前馈控制算法相比于PI控制算法能够使伺服机构的隔离度数值显著减小，说明该算法能够实现稳定精度的有效提升。