常微分方程求解中改进遗传算法的应用

刘艳云

（阳泉师范高等专科学校 山西·阳泉 045200）

在学术研究或工程应用中，建立数学模型解决实践问题是极为普遍的方式。但在利用常微分方程或微分方程组时，除少数特殊类型的微分方程能够快速解析并得到较为精准的数据类型之外，其他多数方程组在解出数据信息时存在一定的困难，所得数据结果也仅为无限接近于真实情况的近似值。由于实践问题类型复杂多样，且无法针对其中的复杂因素加以排查，因此在实际研究过程中，必须针对复杂函数的运算过程加以改善，将其求解近似值的难度加以弱化，进而在求解过程中达到快速搜索最优解集的效果，并将其最优解集控制在精度较高的范围。而运用遗传算法便是其中极为重要的求解思路，通过优化解集路径，并对比分析其中数据模型的契合度，从而在进一步优化解集条件时，改善最优解集方案的流程，提高最终取值范围的精确性。

一、应用改进遗传算法解析常微分方程的优势

（一）遗传算法的运算机制

遗传算法的英文全称为：Genetic Algorithm，传统意义的遗传算法是模拟达尔文生物进化论中的自然选择学说和遗传学机理而设计的生物进化计算模型。将遗传算法应用于常微分方程并未改变其原本的运算机制，也是以模拟自然进化流程寻找和搜寻最优解集的方案，明确常微分方程的解题路径。遗传算法所描述的是潜在解集存在的最优种群，而每一个种群都具有相应的基因编码个数，适用于常微分方程在常规条件下的适应个体解集。在相对独立的解集中，势必存在遗传因子的适应度问题，如果适应度较强，则说明染色体具备了优先选择机制，能作为最优解集输出，得到常微分方程的最优解决方案。而适应度较弱，则代表该染色体并不具备最优解集特征，需要在运算流程中予以剔除。利用遗传算法的最优解集寻找方案，能在进化过程中摒弃并不重要的普通解集，有选择性地开发具备遗传特征的最优解集。因此，在种群迭代反映后，最终从优胜劣汰的演化机制中不断接近于最优解集的特征，便可逐代演化产生近似解，且在每一代个体适应度上不断接近遗传因子的最佳运行状态，并从中筛选出具有遗传特征的常微分方程最优解。通过组合交叉、变异等过程，子代继承了父代优良基因，而并未脱离解集种群原有的运算条件，因此其解码过程更加契合常微分方程的求解需求，体现了优化运算流程和适应度的优势，对于强化常微分方程的最优解集甄选具有支持作用[1]。而这样的遗传进化过程，也相当于将导致种群解集运算偏差的不利因素进行剥离，从而契合自然进化的种群迭代演化机制，形成更加适应全新后代种群生存条件的客观环境。因此，末代种群中必然存在常微分方程的最优个体，该个体也是在诸多解码程序中最终得到的最优解集，满足了常微分方程所有求解需求，是优化解题路径和强化常微分方程解析环境的有效方式，得到的结果也可以作为常微分方程问题的近似最优解。

（二）应用遗传算法解析常微分方程的优势

改进遗传算法，是针对对常微分方程求解近似值过程中的简化模式。基本应用思路是：运用最小二乘原理，并综合运用微分方程的函数模型，将求解问题转为求解最小取值范围的函数问题，从而利用改进后的遗传算法优化问题类型，简化运算步骤与时间，并提供完整的最优解集条件。

对于部分多目标、多模型、非线性的函数解题优化路径而言，应用遗传算法是优化解题路径的过程，而且针对不可微和存在多峰值的函数类型，其他算法的求解过程更为繁琐，难度也更大。由于遗传算法本身具备更高的并行运算条件，所得数据类型的分段运算结果具有随机性，故其自适应能力较强，可以优化全局解集的搜索概率与范围，进而得到最优解集的可行性方案。因此，应用遗传算法解析常微方程是优化求解路径的有效方式之一，可以提供完整的解题思路与最佳解集方案。

将常微分方程求解的流程转化为最优化解集方案的模式，是利用遗传算法构造近似方程组的解析模式，所以可以在最大程度上优化方程解集的取值范围，也是应用遗传算法优化常微方程解题流程的有效措施。

（三）简单的函数优化方向

设函数f（x）为x=a的临近区域，在取值范围内以n+1为阶，可推导出位于临近区域的任意点x的点集空间，令a与x以及之间存在函数关系：

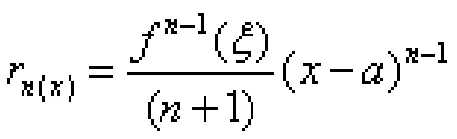
依据此公式，能明确多项式函数的取值空间，并由此空间构造常微分方程的解集范围，所得多项式函数的取值空间就是相对简化的函数χ，在其自身乘积范围γn中作为线性组合所得到的具有函数特征的数值。利用这一函数空间，能令函数形式简化，从而在应用过程中逐步简化，从而得到相对简易的函数特征，这一特征也是优化计算机算法实现快速解集构建的主要方式。尤其这一函数空间已经无限接近于所有函数的近似值，因此其函数表达能力较强。但在边界处理数据条件时，更加倾向于罚函数处理方案，以常微分方程解析流程的转化，促使问题逐步最优并得到最佳解集的取值范围，具体实现流程为：

首先，构建数据集合 M（x,wo,w1,…,wk）=w0+w1x+w2x2+…。类似形式的函数近似值是常微方程在求解过程中逐步优化的参数变量。对于x,wo,w1,…,wk的集合而言，其参量的优化方案也有助于提高后续运算的便捷性。

其次，在选择多项式的函数近似值时，其常微分方程本身的解集范围也相对明确，并从中提取最为简单的解集方案。可以利用多项式函数的取值范围锁定最小二乘解的取值空间，具体实现方法可以构建Ⅳ个等距节点的函数模型，函数表达式为：

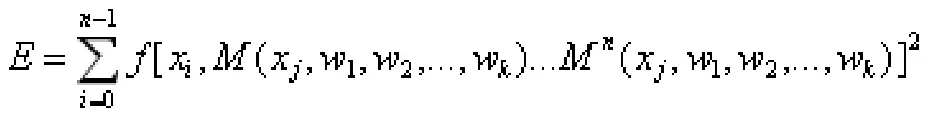
最后，在边界条件相对明确后，可由构造的罚函数模型约束其最优化解集的取值空间，将类似问题转化为并不存在约束条件的最优化解集。因此，其罚函数可以完成基本运算模式的推导，并能强化与之前解集取值范围的对比效果。

此外，设 E,P为针对（x,wo,w1,…,wk）的函数参量，其近似值令的解集范围更为精准，因此所得函数解集为解集组中那个最优化方案，它支持运算条件的不断优化与改善。在运算过程中，令V=E（M）+αP（M）为最小取值空间，其中以α代表正函数的取值范围，同时得到 α=1，x1，x2，…，xn-1 无限趋近于[a，b]的常微函数运算条件。因此，利用遗传算法，能有效降低常微函数方程的求解难度，并以最小值函数运算的方式优化求解流程。

二、常微分方程求解中改进遗传算法的应用

设常微分方程应用遗传算法的函数表达式为：Y=-1/5y+exp（-x/5）cosx，y=0，x 无限接近于[0,1]。 该函数方程可以作为遗传算法在常微分方程求解过程中的优化方案，通过构建数据集合的方式明确近似值的取值范围。因此，常微分方程组的多项式经过特定的解题次数，就能完成多项系数的归集。求解初始条件y=0的常数项，相当于约束了取值空间的具体范围。基于此，多项系数均可以利用遗传算法的模型逐步进化，并得到最优解决方案。可以利用遗传算法模型编写优化函数的文件M，同时令M文件生成平行向量，并得到初始标量的运算条件。在平行向量内的目标函数长度是由相对独立的变量基数决定的，并依据遗传算法在各个参量中的取值范围锁定函数目标，其中包括变量个数、种群大小及其优化条件，交叉概率以及种群迭代次数等一系列优化求解的运算环境。

在遗传算法工具箱中，分别设number of variables 的取值为 1，2，3，…，7，相当于分别构建了完整的多项式近似方程的解集，运算结果在很大程度上符合了三次多项式的求解要求，更加适用于最小值的求解流程，因此由适应度的取值范围扩大便可说明其运算规律的优化形式已经得到改善。其中，适应度值越小，它所代表的函数求解方向越接近于精确解，因此相应的解集中构造三次多项式的运算方案也会快速得到近似方程，并通过遗传算法得到精准度更高的解集。

（一）群体规模对遗传算法最优解集寻找效率的影响

当群体规模存在相对较小的取值范围时，遗传算法所具有的搜索空间极为有限，而个体解集之间由于缺乏多样性，并不容易快速获取最优解集。但当群体规模逐步扩大并增加到涵盖了更多运算信息与条件后，遗传算法的进化条件得以补充，因此可以快速搜索到更多的解集范围。因此，在个体空间的基础数量不断增加与迭代累积时，获得最优解的可能性反而更高，得到近似于最优解的取值范围相对缩小，并无限接近于常微分方程的求解需求。基于改进后的遗传算法能为常微分方程求解提供更多的解集类型，并筛选出并不适应当前数据集合的参考值[3]。因此，当种群大到一定程度时，遗传迭代的最终结果也会不断优化其取值空间的合理性。

（二）交叉概率角度对遗传算法收敛性的影响

从交叉概率角度对遗传算法的收敛性进行评估，能从微分方程的影响中发现：当交叉概率和搜索空间相对较小时，遗传算法很难从中快速提取最优解集。但在交叉率不断增加时，遗传算法在寻找最优解的过程中也会不断提高发掘几率。如果交叉率过高，这样的现象并不会持续，此类现象与遗传算法过度扩增其搜索范围与解集空间有关。如果忽略了微分方程的局部特征，或者搜索区域的稳定性与集中性，同样也无法快速寻找到最优解集。相关研究表明，将交叉概率尽量控制在0.65至0.85的取值范围时，才能够达到预期的收敛效果，才能为寻找最优解集创造便利条件。

（三）进化代数对遗传算法收敛效果的影响

从进化代数对遗传算法收敛效果的影响中能够发现，随着进化代数的不断增加，收敛效果有可能发生好转的现象。但当进化代数不断扩增至较高范围时，反而会降低运算效率或频次，令实验现象无法充分显现。如果运行时间不断增加，遗传算法中的进化代数也会不断上升。将所有参数全部设为依据遗传算法而得到的最优解集时，早期代数信息中个体离理想值仍然较远，那么遗传算法所寻求的最佳值也会被迅速发掘。因此，对于遗传算法，后代中多种群解集越接近于最佳点时，最优解集的可利用价值越高，最佳值改进的效果也相对放缓。最终求得的代优化参数为精确解集的理论参考值，将精确解和近似解进行比较，发现求得的近似解在定义域内，且不存在与定义域外精确解的近似度，因此其最优解集的运算效果更为明显和突出。

结语

综上所述，在众多工程技术问题中，纠结于常微分方程求解的数学形式并无法快速消解其中的解题难度。求解流程中应用遗传算法，能以不断演化和衍生出的子代信息优化父代解集中的缺陷，同时令常微分方程的求解能力更强，所得解集更加接近于实际情况，进而支持由求解问题向最优解集问题的转化，支持求解精度的进一步提升。对常微分方程求解中改进遗传算法的应用进行分析能够发现，群体规模对遗传算法最优解集寻找效率的影响，交叉概率角度对遗传算法的收敛性影响，进化代数对遗传算法的收敛效果影响，都是在最大程度上优化遗传算法最优解集寻找速度的刺激方式。因此，在拓宽遗传算法的适用范围后，能为微分方程的求解提供全新的运算环境，从而实现微分方程求解速度的优化，进一步证明遗传算法在求解最优化问题的有效性，并最终完成微分方程的求解，提高微分方程的求解精度。