模糊识别模型在橡胶坝工程安全评估中的应用

2018-11-06朱红军范衍琦胡继成刘华强

水利与建筑工程学报 2018年5期

朱红军，范衍琦，宋力，胡继成，刘华强

(1.江苏省水利科学研究院，江苏扬州 225002； 2.宿迁市水务局，江苏宿迁 223800)

闸坝工程安全评估[1]因其自身结构功能的复杂性，需结合工程现状调查分析、现场安全检测和工程复核计算这三项成果来综合评判,其实质也是多准则的闸坝结构可靠度评定的过程。在闸坝安全等级评估中先后建立了专家评估法、专家系统法、标准比照评价法、层次分析法、灰色评估方法和加权递阶评估法等。陈守煜等[2-4]创建的系统模糊决策的可变模糊集理论广泛应用于水文水资源、环境、土建工程、化工和社会经济系统，亦可用于水利工程安全评价，如水闸[5]、河道健康[6-8]等。上述各种方法对橡胶坝工程的安全评估却尚未见到相关文章，本文在获得橡胶坝各构件服役情况检测结果的基础上，对比各种评估方法的优劣，参考陈守煜创建的可变模糊集理论，将模糊模式识别模型引入到橡胶坝安全评估中，判断其在正常使用和维护条件下的安全性和适用性。

1 模糊识别模型简介

已知待识别样本的多个指标特征值和多个级别的指标标准，计算与识别样本指标属于相关级别标准模式的相对隶属度，确定各指标值的权重，计算样本级别特征值，评价样本属于哪一级标准模式[6]。根据工程运行管理现状确定评价因素的权重[9]是模型建立的核心，据此可以获得满意的评估结果。建立模糊模式识别模型主要分为以下几步。

1.1 将各个评价指标值规格化

对可分c个评价级别的模糊概念A进行识别的n个样本，每个样本均有m个指标特征值，则相应的指标特征值和指标标准特征值矩阵为：

X=(xij)；i=1，2，…，m，j=1，2，…，n

(1)

Y=(yih)；h=1，2，…，c

(2)

在进行识别之前先将指标特征值变换为对模糊概念A(本文为橡胶坝工程安全)的指标相对隶属度，即消除指标量纲差异。对于越大越优型或越小越优型指标，其计算公式有多种，本文根据需要采用式(3)和式(4)：

(3)

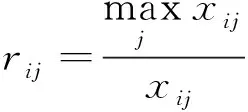
(4)

无论越大越优或越小越优型指标标准特征值，均可利用公式(5)得到级别h指标i的标准值yih对模糊概念A的规格化数：

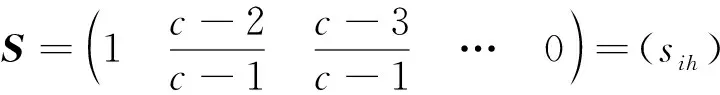
(5)

经规格化处理后可得指标特征值与指标标准特征值规格化矩阵为：

R=(rij)； 0≤rij≤1

(6)

S=(sih)； 0≤sih≤1

(7)

1.2 确定指标权向量

其确定方法[10-11]可从识别的安全性与样本的整体性进行考虑。具体方法如下：

(1) 确定指标重要性的定性排序。通过征询若干位相关专业的专家意见，进行关于重要性的定量、定性评价指标二元比较，列出定性排序标度矩阵E

(8)

(2) 标度矩阵E的一致性检验。根据一致性条件(若ehk>ehl时，计ekl=0；若ehk

(3) 确定指标对重要性的相对隶属度。根据实际工程情况，以矩阵各行和数最大排序数所对应的目标为准，应用表1所述语气算子[11]分别与其余目标进行比较。可得各指标对重要性的相对隶属度。

(4) 归一化处理，得归一化权向量。

(9)

表1 语气算子与模糊标度、隶属度对应关系[11]

1.3 计算样本对级别h的相对隶属度

样本j与级别h之间的差异可用广义欧氏权距离式(10)表示：

(10)

将R中的相对隶属度rij分别与矩阵S中的行向量逐一比较，得级别上下限aj和bj。相对隶属度所构成的矩阵即为模糊识别理论模型：

(11)

α为模型优化准则参数，p为距离参数，本文中α等于2，p等于2。样本归属于各个级别的相对隶属度矩阵为：

(12)

从而计算样本的级别特征值并对其进行综合评价：

(13)

2 应用实例

2.1 橡胶坝的基本情况

某橡胶坝[13]建成于2001年，该坝为充水枕式橡胶坝，长30 m，高1.6 m，底板高程21.1 m(废黄河高程)；坝底板、消力池及两侧翼墙底板均采用素混凝土结构，强度为C20，上游铺盖、下游护坦及上下游翼墙墙身采用浆砌块石结构，充水泵房和坝袋端部扶壁式挡墙采用C25的钢筋混凝土结构。2014年将原来柴油机充水机泵更换为电动机。2016年夏季橡胶坝在排涝过程中发生下游护坦冲毁、消力池部分冲毁、下游右侧翼墙部分底板掏空险情。

2.2 橡胶坝评价指标与评价标准

以橡胶坝工程现状调查和安全检测过程为实例,拟选取该坝底板混凝土强度x1，扶壁翼墙的混凝土强度x2、碳化深度x3和保护层厚度x4为定量评价指标；坝袋材料老化x5、塌肩漏水x6、上下游浆砌石翼墙x7、消能防冲设施x8、冲排设备x9和工程管理能力x10为定性评价指标。定量指标采用现场检测数据，定性指标根据专业经验采用百分制进行评分,定性指标评价标准和分级评分区间见表2，取五位专家对定性指标打分平均值为定性指标特征值，评价指标特征值见表3。

表2 橡胶坝安全与各指标标准区间值的关系

表3 橡胶坝工程分级指标值

按照式(3)、式(4)、式(5)计算指标特征值和指标标准特征值的相对隶属度矩阵R=(1.00，1.00，1.00，1.00，0.22，0.49，0.55，0.28，0.85，0.64)

S=(1 2/3 1/3 0)=(sih) ∀i

通过公式(8)可以计算出含10个特征指标的标度矩阵E

矩阵E各行之和依次为4.0，2.5，1.0，1.0，9.5，8.5，7.5，4.0，6.0，6.0。从由大到小的排列得出评价指标关于重要性的排序为x5>x6>x7>x9=x10>x1=x8>x2>x3=x4，排序中冲排设备和工程管理能力同样重要，底板混凝土强度和消能防冲设施同样重要，扶壁翼墙碳化深度和保护层厚度同样重要。

归一化后权重向量为

w=(0.070，0.052，0.023，0.023，0.210，0.155，0.140，0.101，0.113，0.113)

根据式(12)、式(13)编写MATLAB程序计算各个级别的相对隶属度矩阵和级别特征值为

U=(0.1017，0.3533，0.4258，0.1192)

H=(1，2，3，4)·UT=2.563

根据H对橡胶坝安全评估，由文献[2]知评价规则H∈[c-0.5，c+0.5]，则将评价区域归于c类。故该橡胶坝安全评估等级为3级，偏于2级。

根据规范[14]规定，运用指标达不到设计标准，工程存在严重损坏，经除险加固后，才能达到正常运行。由于橡胶坝袋整体严重老化，端部塌肩漏水现象突出，下泄水流将海漫护底完全冲毁，危及到橡胶坝整体的稳定安全。可整体更换橡胶坝袋，并对消能设施和冲毁的部分翼墙进行除险加固。