欧拉积分余元公式的证明及应用
2018-11-06熊骏
长江大学学报(自科版) 2018年21期
熊骏
(长江大学信息与数学学院,湖北 荆州 434023)
1 欧拉积分的余元公式
欧拉积分是《数学分析》[1~3]中含参量反常积分中的一种,包括伽马函数与贝塔函数,其表达式分别为:


通过变量代换可得到贝塔函数的另外2种表达式:
欧拉积分都在定义域内内闭一致收敛,具有很好的性质,如在定义域内连续、可导等。由变量代换及分部积分法可以得到它们的性质及递推公式:
Γ(s+1)=sΓ(s) (s>0)
Γ(1)=1Γ(n+1)=n!
Β(p,q)=Β(q,p) (p>0,q>0)
伽马函数与贝塔函数的关系式如下:
欧拉积分的余元公式[4]为:
下面,笔者结合幂级数与傅里叶级数及复变函数中的留数给出余元公式的2种证明。
2 余元公式的证明
2.1 第1种证明
由:
当0 从而: 即: (1) 下面考虑将cosπx在[-α,α]上进行傅里叶级数展开,首先将其周期延拓为周期为2α的周期函数。又cosπx在[-α,α]为偶函数,其傅里叶级数为余弦级数,且傅里叶系数为: 由傅里叶级数的收敛定理有: 特别地,取x=0得到: 化简得: (2) 比较式(1)和式(2)可得余元公式: 由: (3) 而: 且: 由式(3),令R→+∞,ε→0得: 即: 于是: 由余元公式有: 注:n=4,m=1时即为例1。 解这是含有瑕点a,b的反常积分,由于: 由柯西判别法知,该反常积分收敛。 令x=a+t(b-a),则dx=(b-a)dt,当x=a时t=0,当x=b时t=1。于是: 余元公式是欧拉积分的一个重要公式,其证明还有许多方法,其应用也非常广泛。由于伽马函数可以延拓,因此还可以研究更一般情况下的余元公式。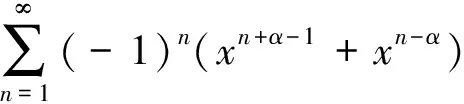
2.2 第2种证明

3 余元公式的应用







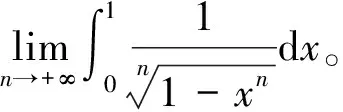

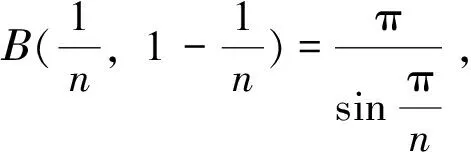
4 结语
