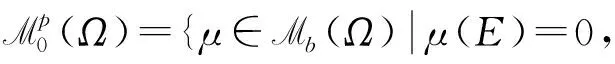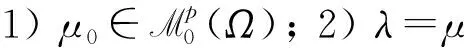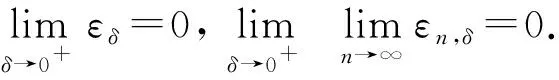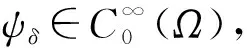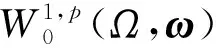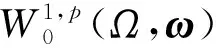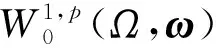一类具权函数的退化椭圆方程解的性质
2018-11-06代丽丽曹春玲
代丽丽, 曹春玲
(1. 通化师范学院 数学学院, 吉林 通化 134002; 2. 吉林大学 数学学院, 长春 130012)
0 引 言
椭圆方程在几何学、 电磁学、 弹性力学和流体力学等领域应用广泛. 椭圆方程分为线性与非线性两类, 目前, 关于非线性椭圆方程的研究已得到广泛关注. 除几类特殊的方程及有特定定解条件的方程外, 给出非线性椭圆方程的显示解非常困难, 需要通过其他途径表达一个非线性椭圆方程刻画的物理意义及内在规律. 研究非线性椭圆方程解的适定性问题, 即研究其解的存在性、 唯一性和正则性等. 目前, 解决该类问题的方法主要有不动点定理、 单调性方法(也称为上下解方法)、 拓扑度理论[1]、 临界点理论[2-6]和变分法[7-8]等. 本文考虑一类具权函数的退化椭圆方程
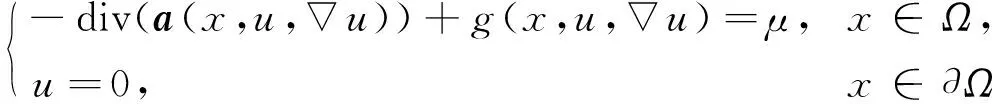
(1)
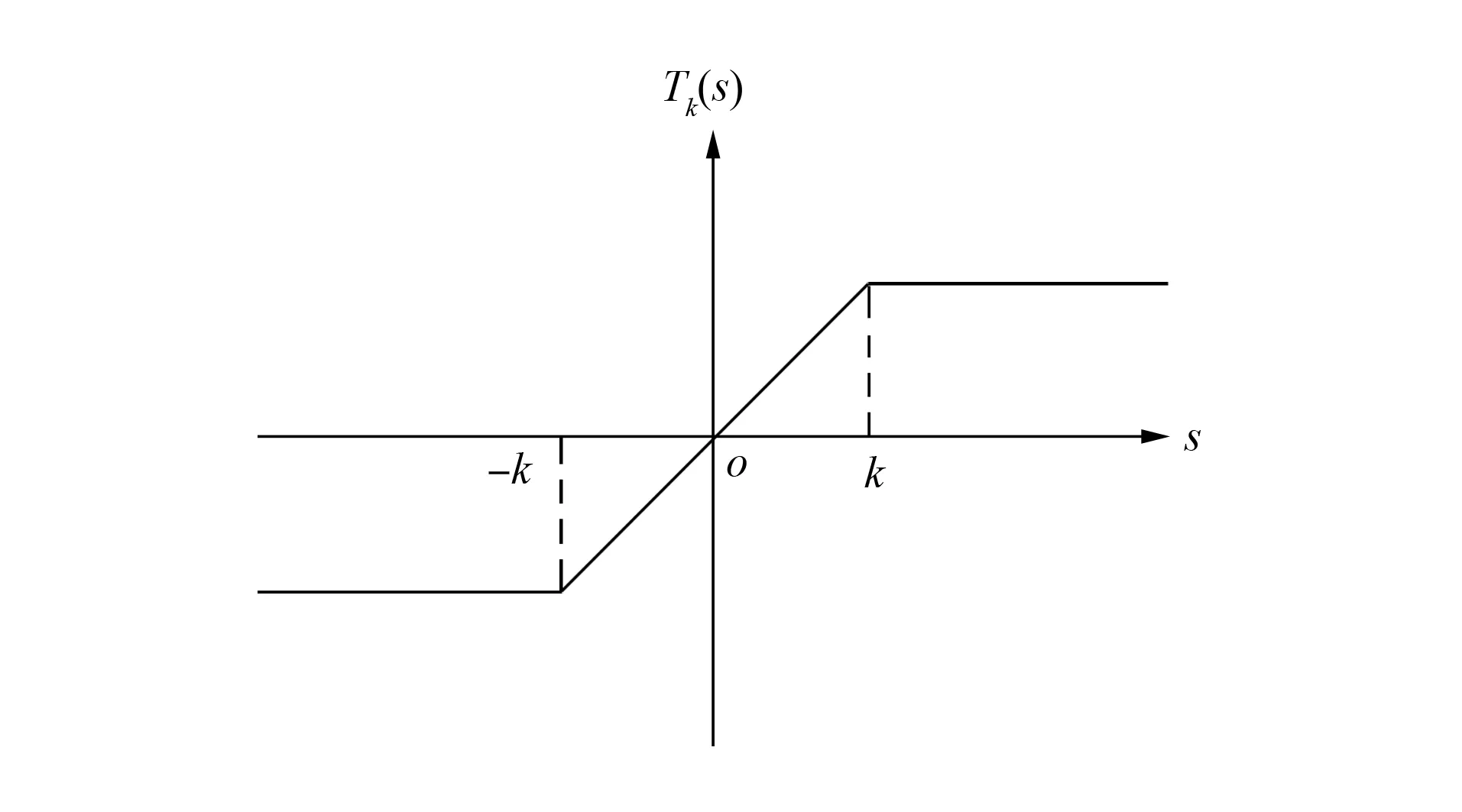
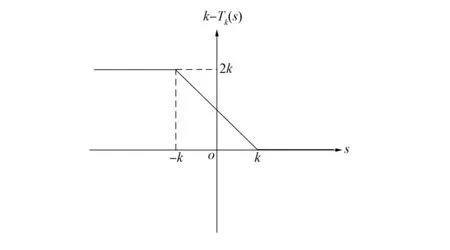
解的性质. 其中:Ω是N(N≥2)中的有界区域;为加权的Sobolev空间,ω(x)为权函数,p是满足1 (H2)a(x,s,ξ)={ai(x,s,ξ)}1≤i≤N:Ω××N→N是一个Carathéodory向量值函数, 对任意的s∈及几乎所有的x∈Ω和每个ξ∈N, 以下不等式均成立: (2) (3) [a(x,s,ξ)-a(x,s,η)]·(ξ-η)>0, ∀ξ≠η∈N, (4) 其中:k(x)是Lp′(Ω)中的一个非负函数;p-1+(p′)-1=1;c0,c1为正数; (H3)g(x,s,ξ)是一个Carathéodory函数, 对任意的s∈及几乎所有的x∈Ω和每个ξ∈N, 满足 g(x,s,ξ)sgn(s)≥0, (5) (6) 其中:b:+→+是一个连续增函数;d(x)是L1(Ω)中的非负函数. k-Tk(s)定义为 其函数图像分别如图1和图2所示. 图1 Tk(s)的函数图像Fig.1 Functional image of Tk(s) 图2 k-Tk(s)的函数图像Fig.2 Functional image of k-Tk(s) 引理1[11]设g∈Lr(Ω,γ),gn∈Lr(Ω,γ), 且‖gn‖Lr(Ω,γ)≤c, 1 引理2[11]假设条件(H1)成立,G:→是一致Lipschitz连续函数, 且若G′不连续点的集合D是有限的, 则 (x,u,u)·vdx, (7) (8) 对每个Ω中的紧子集K, 定义K关于Ω的p-容量集为 其中:χK是K的特征函数. 记inf Ø=+∞.Ω的任意开子集U的p-容量集定义为 capp(U,Ω)=sup{capp(K,Ω),K是紧集,K⊆U}; Ω的任意开子集B的p-容量集定义为 capp(B,Ω)=inf{capp(U,Ω),U是开集,B⊆U}. (9) 根据文献[14-15]可得如下结论: 定理1设E是Ω中的Borel集, 满足capp(E,Ω)=0,λ∈Mb(Ω)是集中在E上的正测度,fn是L∞(Ω)中的非负函数序列, 满足 (10) g满足式(5),(6),un是方程 (11) b(k)k≤c0/2, (12) 其中b由式(6)定义. 由于b是连续函数, 因此存在k使得式(12)成立. 在式(8)中选取一个检验函数[14-15]v=(k-Tk(un))ψδ, 有 下面分别估计I1,I2,I3,I4. 对于I2, 由k-Tk(un)在L∞(Ω)中弱*收敛于k-Tk(u)且在Ω上几乎处处收敛可知,ψδ(k-Tk(un))在(Lp(Ω,ω))N中强收敛于ψδ(k-Tk(u)), 结合式(9)中第一个等式, 有 (13) 对于I3, 当un>k时,k-Tk(un)=0, 结合式(5), 可得 由式(9)可知,ψδ在L∞(Ω)中弱*收敛于0. 通过选取适当的k, 并结合式(12), 有 同时, 通过选取适当的k, 有 整理得 对于I1, 结合式(2), 有 由于I4非负, 因此可去掉非负项, 并结合I1,I2,I3的估计, 可得 即 (14) 若在式(8)中选取v=Tk(un)(1-ψδ)作为一个检验函数, 则有 对于J3, 由于Tk(s)与s同号, 因此结合式(5), 有J3≥0. 同时, 类似估计I2的方法, 可得J2=εn,δ. 对于J4, 结合式(11)中第二个等式及式(10), 有 对于J1, 结合式(2), 可得 (15) (16) 证毕.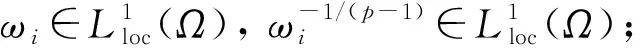
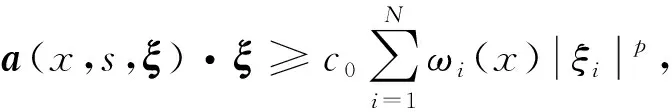
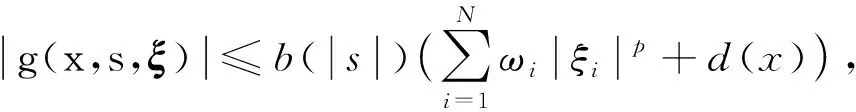
1 预备知识
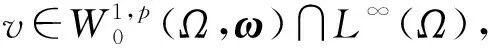

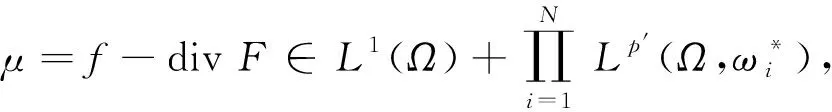
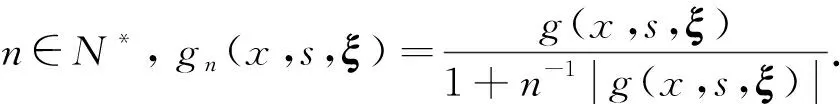
2 主要结果