基于深度卷积神经网络的极化雷达目标识别

盖晴晴 韩玉兵 南华 白振东 盛卫星

(1. 南京理工大学,南京 210094; 2. 北京航天长征飞行器研究所,北京 100076)

引 言

雷达高分辨一维距离像(high resolution range profile,HRRP)是用宽带雷达信号获取的目标各个散射点子回波在雷达视线方向上投影的向量和幅度波形[1],包含了目标的重要特征结构信息,而且具有易获取实时性强等特点,是雷达目标识别的重要特征. 但HRRP具有方位敏感性,即目标的姿态角发生微小的变化时,目标散射中心的分布就可能发生较大的变化,从而导致距离像形状发生很大变化[2]. 所以本文将极化信息和高分辨一维距像相融合,组合成极化距离矩阵,对雷达目标进行全方位的特征提取与建模．该方法可以有助于减少HRRP的方位敏感性带来的影响,且因极化信息的加入,使得我们可以获得更加丰富的雷达目标信息[3]. 实际上多极化的HRRP被运用在多篇研究HRRP的论文中. 文献[4-5]提出了距离极化多维匹配识别算法,该算法将4组不同极化下的HRRP以某种规则进行融合扩展,最后利用相关匹配或者模糊匹配的方式进行目标识别. 文献[6]是提取了目标特征尺寸、散射中心分布熵和强散射中心维数3种目标特征,然后根据这3种特征的分类信息进行了融合识别. 文献[7]将4组不同极化下的HRRP分别进行目标的分类与识别,最终的结果是根据多数投票准则进行决定. 文献[8]利用D-S证据理论将极化信息和距离信息有效结合起来. 以上方法均有一个问题,即仅对极化距离矩阵进行了某一方面的研究. 针对极化雷达数据,本文在文献[4]的基础上,利用Pauli分解理论[9]和Freeman分解理论[10]对极化距离矩阵进行目标特征的提取,以获得更多有效的雷达目标特征.

目前,深度学习已经成为了互联网大数据和人工智能的一个热潮. 其通过建立类似于人脑的分层模型结构,对输入数据不断地进行无监督的学习与训练,提取更高维数的特征,在语音[11]、图像[12]、自然语言[13]、在线广告等领域取得了显著的成效. 当然,近年来,深度学习被广泛应用在目标识别领域. 谷歌的虚拟人脑[14]、ImageNet数据库[15]、图像的同时分类和标注[16-17]、视频中的动作行为识别[18-19]在深度学习的模型上均取得了较好的效果. 本文将深度学习运用到雷达目标识别领域[20],将提取得到的雷达目标特征向量以张量形式的数据结构送入卷积神经网络进行更加深一步的特征提取和目标识别. 该方法不仅充分地利用了极化信息,还能通过深度神经网络不断的自我学习与监督进一步提高雷达目标的识别效率.

1 基于极化距离像的特征提取

在宽带多极化雷达体制下,对目标进行一维距离成像,可以获得4 种极化组态(如HH、HV、VH、VV)下的HRRP. H、V分别表示水平极化、垂直极化,PQ(P、Q=H或V)表示P极化发射,Q极化接收的组合状态. 设目标4 种不同极化组态的HRRP为

{XPQ(k)|k=0,1,…,N-1;P=H,V;

Q=H,V}.

(1)

式中:k为距离单元;N为径向距离长度.

定义极化距离矩阵为

(2)

对于极化距离矩阵X,将XHH和XVV称为同极化项,而XHV和XVH称为极化交叉项.在满足互易条件时,即XHV=XVH,此时极化距离散射矩阵X可以表示为

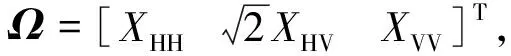
(3)

Ω是复散射矩阵．定义其协方差矩阵C为

(4)

式中:L表示目标视角数;〈·〉表示在多视角空间的平均处理;*表示共轭操作;H表示共轭转置. 可以看出协方差矩阵C是Hermitain矩阵,只包含6个独立的元素:3个表示能量的实数对角线元素,3个独立的复数元素. 所有的极化距离信息都包含在C这6个元素中. 对多视角空间内数据的平均处理有助于减少HRRP方位敏感带来的影响[21].

本文对极化距离矩阵进行目标特征提取的过程主要包括两个方面: 一方面是对极化距离矩阵X直接作处理,包括直接基于极化距离矩阵X的目标特征提取和基于Pauli分解理论的特征提取两种方法;另一方面是基于协方差矩阵C的目标特征的提取,本文所用方法为Freeman分解.

1.1 直接基于极化距离矩阵的特征提取

目标的4种不同极化组态下的距离像为式(1). 为消除幅度增益变化的影响,对距离像进行功率归一化,得到

(5)

考虑同一目标在不同极化组态中HRRP的相关性,将HRRP信息和极化信息有机地结合起来,这里参考文献[4]的做法,将归一化后的HRRP进行如下处理:

X1(k)=YHH(k),

(6)

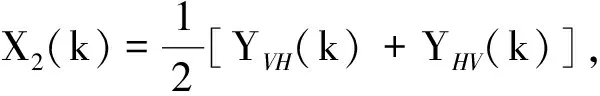
(7)

X3(k)=YVV(k),

(8)

(9)

(10)

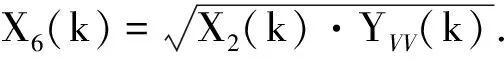
(11)

经由上述处理,得到6个雷达目标特征向量.

1.2 基于Pauli分解理论的特征提取

Pauli是极化雷达目标极化分解的一种以相干理论为基础,算法复杂度较低的算法,其原理是将目标的极化矩阵分解为4个Pauli线性基的相加. 本文将该分解理论运用到雷达目标的极化距离矩阵X上,对X的分解如下:

(12)

在满足互易定理(即XHV=XVH)的情况下,此时Pauli基缩减到Xa,Xb,Xc这三项,即Pauli分解如下:

(13)

由典型目标散射矩阵可知[7],式(13)中:Xa代表平面目标;Xb代表0°定向角的二面角;Xc代表45°的定向角的二面角.

结合式(12)和式(13)可以得到:

(14)

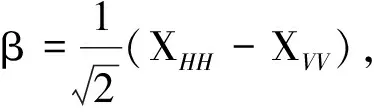
(15)

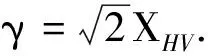
(16)

式中:α,β,γ分别代表目标中平面分量,二面角分量和45°的二面角分量.

由此我们又获得了3个雷达目标特征向量.

1.3 基于Freeman分解理论的特征提取

Freeman分解是一种基于三元散射模型的目标分解,其将协方差矩阵C表示为表面散射、二次散射和体散射3种散射机理的加权和,表达式为[8]

C=fsCs+fdCd+fvCv

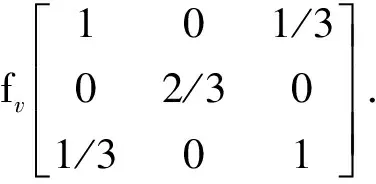
(17)

式中:Cs,Cd和Cv分别为表面散射、二次散射和体散射机理的协方差矩阵;fs、fd和fv分别为相应的加权系数;a和b分别为二次散射和表面散射的参数.

由文献[8]可知三个加权系数对应的功率Ps,Pd,Pv:

Ps=fs(1+|b2|),

(18)

Pd=fd(1+|a2|),

(19)

Pv=8fv/3.

(20)

由此我们获得了另外3个目标特征向量.

本文对雷达目标进行以上3种特征方式的提取,最终每个雷达目标可以获得12个目标特征向量,如表1所示. 为了不破坏目标特征空间结构上的信息和尽量使每个特征提取方法都发挥很好的作用,我们吸取了QI等人在文献[22]中的做法,将这12个雷达目标特征向量结合起来,组成张量的形式. 把利用Pauli分解理论和Freeman分解理论得到的雷达目标特征向量看作是直接基于极化距离矩阵特征提取到的目标向量的补充. 对每个雷达目标来说,最终可以获得一个三维张量F∈RI1×I2×I3的数据,其中I1是目标的角度数,I2是目标的特征向量数,I3是每个特征向量对应的特征维数.

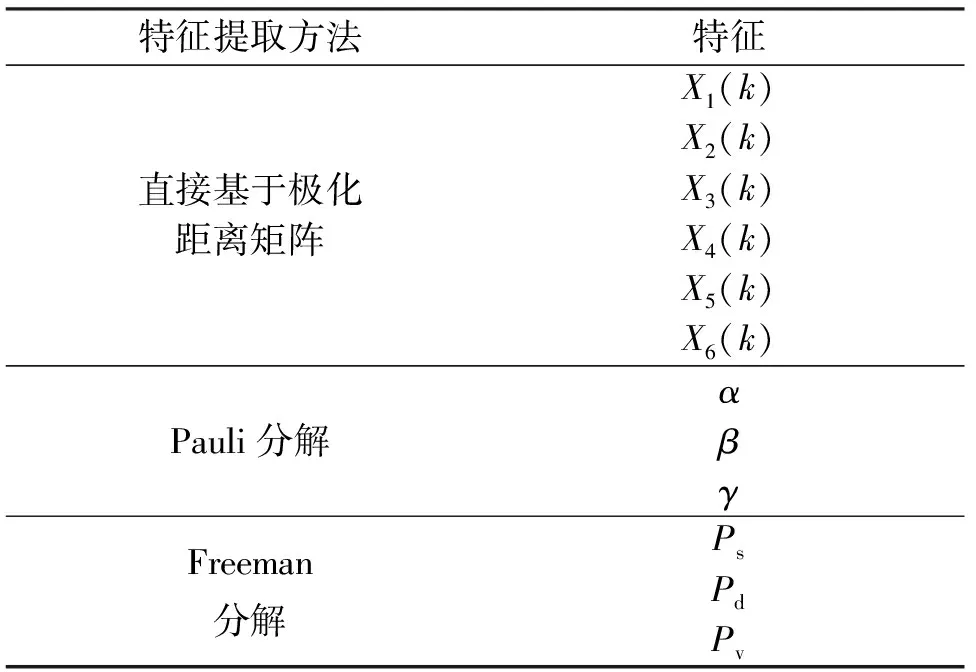
表1 雷达目标特征向量集合Tab.1 Radar target feature vector set

2 雷达目标识别深度卷积神经网络

深度学习最早兴起于图像识别,但是在短短几年时间内,深度学习推广到了机器学习的各个领域,在图像识别、语音识别、音频处理、机器人、化学和金融等各个领域均有应用. 本文拟基于TensorFlow平台将其运用在雷达目标识别方面.

由于卷积神经网络(convolution neural networks,CNN)在图像分类数据集上有非常突出的表现,本文目标特征向量组合灵感来源于全极化合成孔径雷达(synthetic aperture radar, SAR)图像分类[23],对于每个目标最终获得的三维张量形式的数据,我们可以类似地把其数据结构看成图像数据信息的结构,所以拟采用卷积神经网络对由第1节获得的数据集F进行特征提取和目标识别.

2.1 雷达深度卷积神经网络目标数据获取

本文所使用的原始数据是利用Feko软件仿真计算得到的目标的雷达散射截面积(radar cross section,RCS). 用于仿真的目标有3种,分别是圆锥、柱锥和球锥,如图1所示. 目标的长度分别为0.63 m、1 m和2.2 m. 取俯仰角从0°到180°,角增量为0.1°,因此每个目标有1 800个姿态. 测量频率波段为0.2～0.83 GHz,增量为0.01 GHz,共64个频率点,即每个姿态下采64个频点. 在获得目标的4组极化组态下的RCS数据以后,经过逆傅里叶变换获得4种极化组态下的一维距离像(HRRP).4组极化组态分别为水平发射-水平接收(HH),水平发射-垂直接收(HV),垂直发射-水平接收(VH),垂直发射-垂直接收(VV). 所以每类目标有4组极化 组态下的HRRP,每组极化组态下都有1800个姿态,每个姿态有64个采样频点,这4组极化组态下的HRRP就组成了我们之前所述的极化距离矩阵X.

图1 3种目标模型(圆锥、柱锥、球锥)Fig.1 3 target models (cone, cylinder-cone, sphero-cone)

利用第1节所述的3种雷达目标特征提取方法,对雷达目标的极化距离矩阵X进行特征提取,最终可以获得一个三维的张量F∈RI1×I2×I3数据.由于每个单极化距离像的矩阵大小为1800×64,最终每个雷达目标可以获得的数据集为F∈R1800×12×64F∈R1800×12×64,其中1 800表示目标的姿态数,12表示经过3种特征提取方法得到的目标特征向量数,64表示每个姿态下有64个采样频点.

2.2 深度卷积网络结构

这里我们提出的深度CNN如图2所示,总共包含2个卷积层,2个池化层,2个全连接层. 每个卷积层后面接有一个池化层,采用max pooling形式,下采样窗口的大小(pooling size)取2×2,滑动步长(stride)取2. ReLU非线性激活函数作用于2个卷积层,Softmax非线性函数作用于第2个全连接层的输出节点. 卷积层中卷积核的滑动步长全部取值为2.

图2 基于雷达目标特征向量的CNN架构图Fig.2 CNN structure diagram based on radar target feature vectors

我们将训练数据集分批次输入该CNN中,对CNN的参数进行训练. 输入的雷达目标特征向量的大小为12×64,第一个卷积层选取了深度为32,大小为5×5的卷积核,输出为32×12×64的特征矩阵,经过第1个池化层后雷达目标特征向量的大小变为6×32. 将第一个池化层的输出送入第2个卷积层,其深度为64,卷积核的大小为5×5,所以输出特征向量的大小为64×6×32,经过第2个池化层后雷达目标特征向量的大小变为3×16. 最终雷达目标特征向量经过卷积层和池化层的特征处理大小由12×64变成了64×3×16. 第2个池化层经过扁平(flatten)处理以后送入有512个节点的第一个全连接层,其输出再送入Softmax层,得到3个大小为1×1的输出节点,每个节点的输出值对应于每一类别的概率. 为解决训练样本数据少而产生的过拟合的问题,在模型训练阶段将Dropout[24]用于第一个全连接层,L2正则化方法[25]运用于第一个全连接层和第二个全连接层.

2.3 网络训练参数设置

为了综合梯度下降算法和随机梯度下降算法的优缺点,本文采用了这两个算法的折中——每次计算一小部分的训练数据的损失函数,这一小部分数据被称为一个batch,这里batch值设置为45. 采用指数衰减学习率法,初始学习率为0.01,衰减系数为0.99. 为了防止因训练数据过少而产生的过拟合问题,采用L2正则化和Dropout两种方法,Dropout值为0.5,通过反向传播算法微调整个网络的参数. 为了使训练出的网络模型在测试数据上更加健壮,在测试阶段采用了滑动平均模型[25],模型平均衰减率为0.99.

综上所述,本文的算法流程框图如3所示．

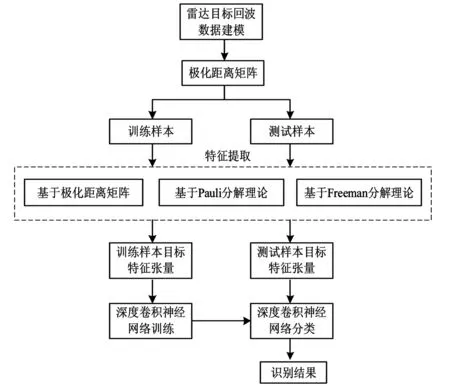
图3 算法流程框图Fig.3 Flowchat of the algorithm

3 实验结果与分析

在进行计算机仿真前,必须先把数据集分为训练集和测试集. 我们有3种目标,每一种目标的数据含有4组极化组态,1 800个俯仰采样点. 因此在每一种极化组态下,我们总共有3(目标种类数)×1 800(姿态数)=5 400个数据,按照它们的姿态分为训练集和测试集. 假定训练集的数据来源于角增量为0.4°的均匀角度采样数据,相当于每个目标取出其四分之一的俯仰角数据,即有1800/4=450个姿态. 训练数据与测试数据数量之比是1/3,即针对整个雷达目标数据集,选择25%的样本作为网络的训练集,余下75%的样本作为测试集,即训练集总共有1 350个数据,测试集总共有4 050个数据. 本文实验数据的信噪比均为0 dB.

为了说明将极化信息与HRRP相结合的有效性,在Matlab平台上进行了基于极化距离矩阵的仿真,并且与只有一种极化组态下的一维距离像进行识别的结果进行了比较. 将极化距离矩阵通过直接基于极化距离矩阵进行特征提取,然后将提取到的目标特征送入支持向量机(support vector machine, SVM)分类器进行分类,结果如表2所示. 这里分类算法采用SVM算法.

表2 基于不同特征的目标平均识别率Tab.2 Target average recognition rate based on different characteristics

为了与以上结果做对比,本文又做了以下4个实验:基于极化距离矩阵的深度卷积雷达目标识别;基于极化距离矩阵和Pauli分解理论的深度卷积雷达目标识别;基于极化距离矩阵和Freeman分解理论的深度卷积雷达目标识别;基于极化距离矩阵、Pauli分解理论和Freeman分解理论的深度卷积雷达目标识别. 为了书写方便,这四个实验名称分别用X、XP、XF和XPF表示.

为了解决基于X、XP(XF)和XPF实验数据维数不同这个问题,本文采用补0的方法,对基于X、XP、XF方法的数据进行补0,以使它们的数据维数和XPF相同. 实验结果如表4～7所示. Step表示训练网络模型所执行的步数,本文每隔100步保存一次网络模型,并用该网络模型对测试数据进行了识别.Loss表示在该步数下总训练样本在该网络下预测值与真实值的差异程度,该值越小说明预测值与真实值越接近, 即在该步数下网络的性能越好.

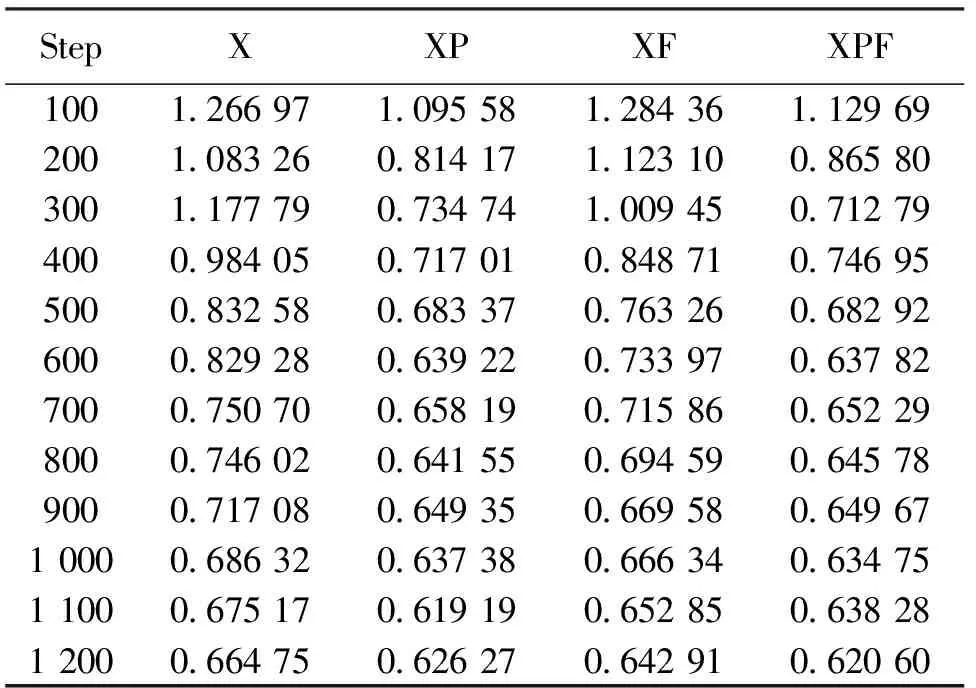
表3 基于不同特征提取方式下不同步数时的Loss结果Tab.3 Loss results based on different steps under different feature extraction methods

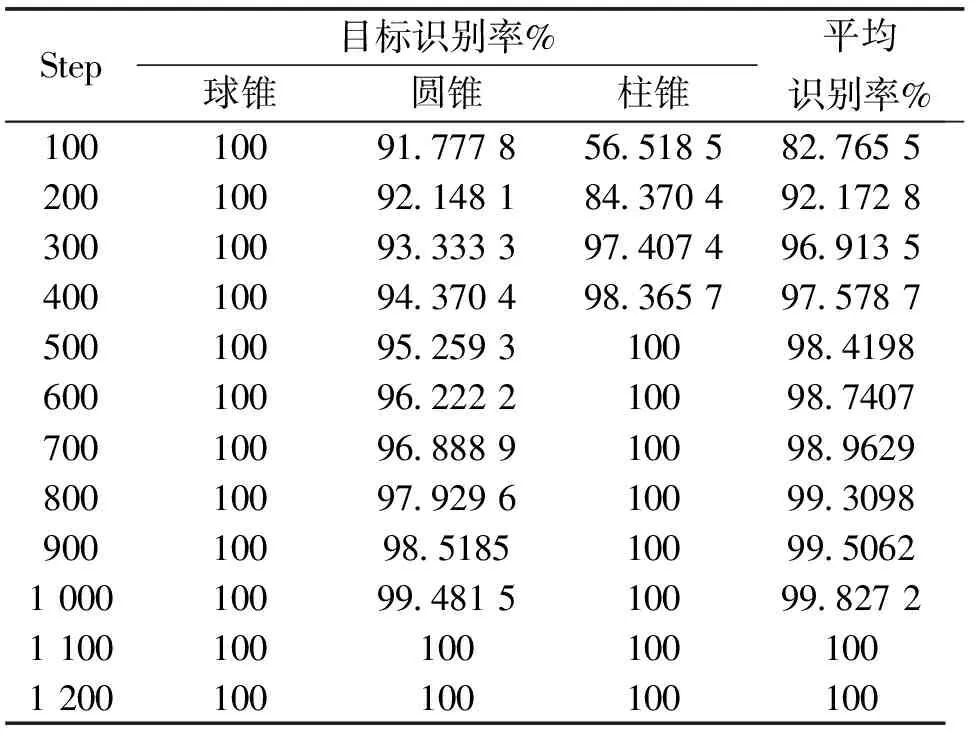
表4 基于X网络不同步数下目标识别率Tab.4 The target recognition rate under different steps based on the X network

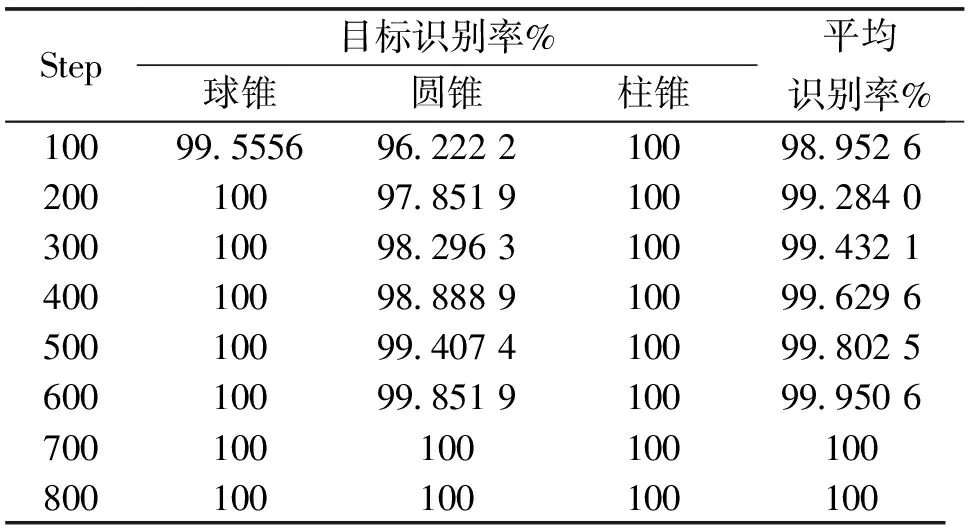
表5 基于XP网络不同步数下目标识别率Tab.5 The target recognition rate under different steps based on the XP network

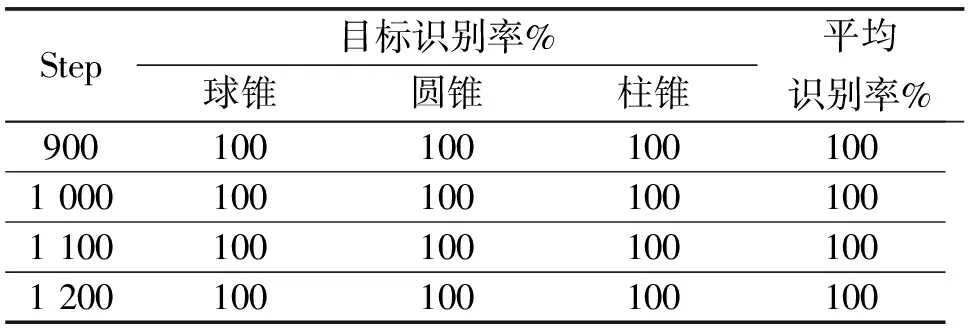
续表5

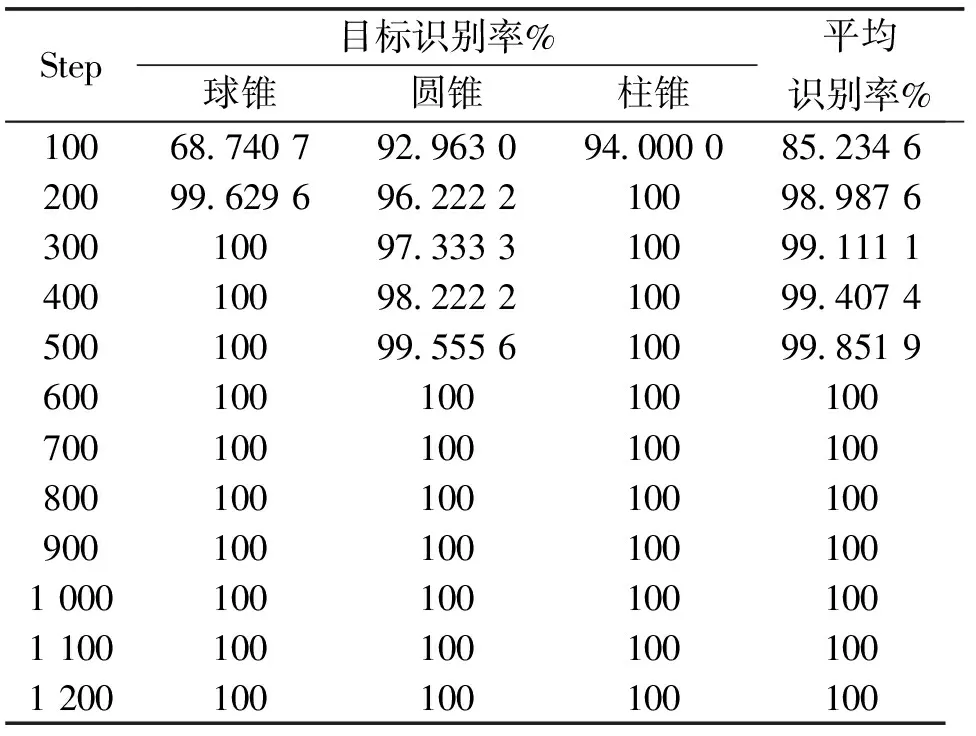
表6 基于XF网络不同步数下目标识别率Tab.6 The target recognition rate under different steps based on the XF network

表7 基于XPF网络不同步数下目标识别率Tab.7 The target recognition rate under different steps based on the XPF network

分析以上实验结果,可得如下结论:

1) 由表2可以看出多极化信息下一维距离像的目标平均识别率要比单一极化下一维距离像的识别效果好.

2) 把Pauli分解理论和Freeman分解理论运用到协方差矩阵C上可以使我们获得更多的雷达目标的本质特征,对雷达目标识别率的提高有很大作用. 由表3可以看出在相同的训练步数Step下,采用不同的特征提取方式,Loss值不同,而且采用XP、XF、XPF的Loss值相对于仅采用X的值要小,采用XPF的Loss值相对于采用XP、XF的值也较小,说明了XPF的网络输出值与真实值更加接近;对比表4、表5、表6、表7,在训练步数较小的情况下,XPF的结果均比在XF、XP、X条件下的雷达目标识别率高,而且目标的平均识别率达到100%所用训练步数从小到大依次为XPF、XF、XP和X,这说明了Pauli分解理论和Freeman分解理论的运用使我们得到了更多有效、更加全面的雷达目标信息.

3) 由表3可以看出,对于每种雷达特征提取方法来说,Loss值的总体趋势是随着训练步数的增加而减少的,由表4、表5、表6、表7可以看出,雷达目标的平均识别率也随着步数的增加而增加直到达到100%,这说明了该深度CNN训练的有效性.

4) 深度CNN在雷达目标识别方面效果显著. 对比表2和4可以发现,均是利用极化距离矩阵对雷达目标进行特征提取,但在训练步数为200时深度CNN的雷达目标识别率比SVM算法的识别率高10.69%,在训练步数达到1 100以及以上的时候神经网络的雷达目标识别率达到了100%. 这是由于相对于传统的机器学习算法,深度CNN能够自动地将简单的特征组合成更加复杂的特征,并使用这些组合特征解决问题,属于深层学习. 而传统的机器学习算法仅使用某种规则对目标进行特征提取然后进行识别,不会对这些特征进行再次的组合,属于浅层学习[24]. 而且,观察表4、表5、表6、表7可以发现,训练步数越大的模型测试数据集的识别率就越高,这得益于深度CNN具有反向传播的特征,训练步数越大网络模型的预测值越接近真实值,而且当训练步数达到1 100时不同特征提取下的雷达目标识别率均达到了100%.

4 结 论

本文利用极化信息与高分辨一维距离像相结合的方式以获得目标的极化距离像数据,然后提出了对其进行直接基于极化距离矩阵、基于Pauli分解理论和基于Freeman分解理论的目标特征提取. 并且将深度卷积神经网络运用到雷达目标识别领域,把获得的雷达目标特征向量结合起来送入深度卷积神经网络进行学习训练. 经过实验与分析,得到如下结论:

1) 极化信息的加入使我们对雷达目标进行了全方位的特征提取与建模,获取了更多的目标信息,大大地提高了雷达目标识别率.

2) Pauli分解理论和Freeman分解理论使我们挖掘了更多包含在极化距离矩阵中的目标信息,这两种方法可以看作是直接基于极化距离矩阵目标特征提取方法的补充.

3) 深度卷积神经网络的运用,以其深层学习的特点使雷达目标识别率得到了质的提高.