超声压气机静/转干涉的非定常模拟研究
2018-11-05王子维
郝 颜, 江 雄, 邱 名, 王子维
(中国空气动力研究与发展中心 计算空气动力研究所, 四川 绵阳 621000)
0 引 言
推重比是航空发动机最重要的性能参数之一。在航空发动机中,压气机级数多,重量大,采用高级压比设计,可大幅度减轻发动机重量,获得较大的推重比提升。为实现高级压比,压气机的叶尖轮缘速度不断提高,这使得压气机部分或全部叶高的进口相对速度大于声速,成为跨声速压气机或超声速压气机。超声速压气机或跨声速压气机叶尖部分受尾迹、激波和叶片扫掠的影响,静转干扰强烈,有必要对其进行深入的探讨研究。
德国人Weise[1]最先进行超声速压气机的探索研究,并于1943年公布了第一台超声速压气机。1946年,NACA的Kantrowitz[2]发布了三种超声速压气机方案的速度三角形,其中一种就是后来得到进一步试验和发展的“内激波式转子”超声速压气机,是当前跨声速压气机转子的原型。1952年,NACA的Klapproth[3]提出“冲压式转子”超声压气机方案,在转子通道内一般不产生或产生较小的静压升,级静压升主要在静子叶排中实现。其后,比利时VKI[4-5]、德国亚琛工业大学[6]也进行了超声速压气机的设计与实验,但普遍存在效率较低、流量偏差较大的问题。国内对超声速压气机的研究始于上世纪八十年代,主要是针对超声速压气机叶片设计和数值模拟研究。肖翔[7]等在研究中将对转压气机与冲压式进气道结合起来,设计并试验了内压式冲压叶栅。邱名[8-10]等提出基于唯一进气角的叶型设计方法,通过数值模拟成功实现多道斜激波加一道正激波的增压方式。王松涛[11]等将叶片抽吸技术应用于超声速轴流压气机中,设计了一种新的低反力度高负荷吸附式压气机,将结尾正激波封在叶栅出口。在大连海事大学,钟兢军[12-13]的研究团队开展新概念超声速压气机研究,探讨旋转冲压压气转子设计及性能影响。
近年来,随着数值模拟技术和实验手段的发展,人们开始关注压气机中转静干涉对性能的影响,Ottavy[14-15]对某跨声速轴流压气机转静叶排干涉数值模拟和试验研究表明:叶栅前缘向上游传播的斜激波会与导叶相互干扰,从而影响叶排间的流动;都昆[16]等对跨声速吸附式压气机的非定常数值模拟研究表明:转静子交界处激波与尾迹的周期性干扰对叶片吸力面附近附面层存在较大影响,非定常效应明显。熊劲松[17]等对压气机级间尾迹的非定常研究表明:上游静子叶排尾迹能够改善转子叶背分离旋涡运动和转子的静压分布,提高级压比和效率。但过去的超声速压气机研究主要考虑级间的转静干涉,转静干扰研究主要是级内上游叶排对下游叶排的影响,且针对超声叶栅的研究较少。
为更加深刻地认识超声速流动下叶排间干扰,本文以预压缩超声叶栅为研究对象,基于课题组自主研发RANS方程解算器,运用非定常数值模拟手段,进行压气机静转子叶栅级间干涉研究。该研究有助于提高对超声速压气机中流动机理的认识,为后续超声速压气机设计提供参考。
1 研究对象及研究方案
1.1 数值研究方案验证
基于对本文数值模拟的可靠性考量,本文先以ARL-SL19叶栅作为研究对象,采用数值模拟和实验数据相对比的方法,对数值模拟方案进行适应性研究。ARL-SL19叶栅由Wennerstrom[18-21]设计,是第一个预压缩叶型。叶栅几何数据及叶栅的试验数据来自文献[22]。此叶栅用于一单级跨声速压气机的转子的第19个S1流面,其所处位置接近叶顶。设计来流相对马赫数为1.616,叶栅弦长为2.733 inch (约69.4 mm),稠度为1.5294,安装角为56.9°,进口气流角为55.58°,出口气流角为53.93°,几何转折角为-2.89°。ARL-SL19叶栅的几何形状如图1所示。但由于该叶栅取自于单级压气机转子,上游没有静子或导叶;同时该叶栅来流轴向马赫数较高,约为0.83,与之匹配的静叶设计较为复杂;且叶栅通道内激波附面层干扰强烈,叶栅损失较大,不具有普遍性,与本文的研究目的不相符,故此叶栅主要用于数值模拟方案校核。

图1 ARL-SL19叶栅Fig.1 Cascades ARL-SL19
本文选用ASPAC软件进行数值模拟,该软件是课题组自主研发的三维可压缩RANS方程解算器。利用有限体积法离散,时间相关的LU-SGS隐式方法求解定常问题,非定常模拟采用双时间步方法[23]。在本文的研究中,对流项空间离散格式选择Roe格式,并利用Condiff限制器进行了线性重构以提高精度;黏性项空间离散格式选用二阶中心离散,时间离散选择LU-SGS隐式格式推进,湍流模型采用S-A模型。
计算网格采用Autogrid5生成多块结构网格,叶栅网格及网格拓扑结构如图2(a)所示。在对网格进行无关性验证后,采用网格单元数量为6万的结构网格进行模拟。其中,前缘点附近的网格如图2(b)所示。为准确求解附面层流动,在叶片型面附近生成“O”型附面层网格,底层网格与壁面的距离为0.002 mm。此算例的y+在0.4左右,在前缘处的y+最大,且不超过2。

(a) Mesh and topology

(b) Mesh near the leading edge
在此研究中,进口边界给定绝对总温、总压、气流角;出口边界给定静压;物面给定轮缘速度。在本验证算例中,给定的进口总压为101 325 Pa,总温为293 K,进气角为0°(即轴向进气),出口静压为可变值,通过调节出口静压,可以得到增压比-总压损失系数曲线。受唯一进气角影响,超声叶栅进口马赫数与轮缘速度有关。此研究通过调整轮缘速度,得到与试验对应的马赫数。在轮缘速度为445 m/s、轴向进气条件下,求得的叶栅进口马赫数为1.6162,与Fleeter[22]的试验马赫数1.616基本保持一致。
1.2 计算及实验结果对比分析

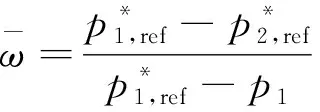
由图3可知,两个软件数值模拟求解的总压损失系数的变化趋势与试验结果完全一致,随静压比增加,总压损失系数先增加,后下降;在设计点附近,总压损失系数最高,实验值为0.151,Fluent求解结果为0.132,ASPAC求解结果为0.143;在压比1.2时,实验测得的总压损失系数为0.049,Fluent的求解结果为0.066,ASPAC的求解结果为0.058。造成这些误差的原因有三方面:一是试验测量时叶片数量有限,叶栅上游脱体激波数量有限,而计算采用周期性边界条件,满足无限叶栅条件;二是实验采用三维直叶片模拟二维流动,会受到叶片三维流动、端壁附面层等因素影响,而基于有限体积法的数值模拟为严格的二维分析,不考虑叶片径向流动及端壁的影响;三是通过求解RANS方程获取流场信息,采用的湍流模型,熵修正、限制器等会影响数值模拟结果;四是实验测量也会存在误差。在这些误差中,实验误差所占例较大。因为除了Fleeter外,Tweedt[24]等也曾对ARL-SL19叶栅进行实验研究。该实验通过在风洞壁面开孔抽吸,移除端壁附面层影响,并抑制栅前激波在洞壁的反射。在马赫数为1.61、静压比为2.15时,试验得到的总压损失系数为0.143,与本文CFD结果相差不大。
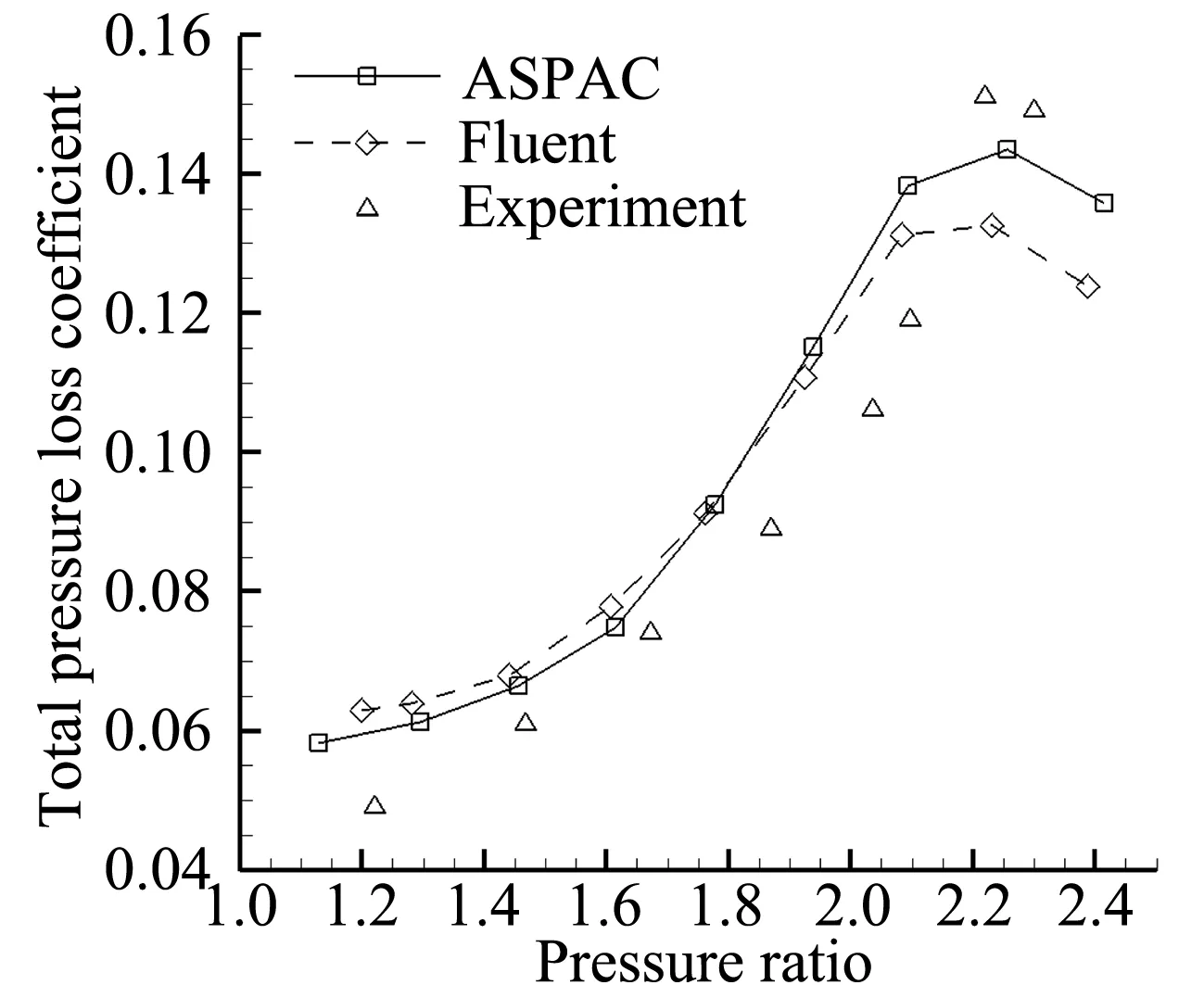
图3 ARL-SL19叶栅的总压损失系数Fig.3 Total-pressure loss coefficient of ARL-SL19
以上结果表明:两个分析软件对ARL-SL19叶栅损失变化趋势的预测结果与试验结果完全一致;对损失具体数值的预测结果与试验结果基本一致;ASPAC的计算结果更接近实验值。因此,采用当前的数值方法和计算网格合理。为保证结果的可靠性,本文后面部分的研究都以此算例网格为模版,采用ASPAC解算器和当前数值模拟方案进行研究。
2 叶型验证
在对超声速压气机叶栅进行数值模拟的过程中,首先针对转子叶栅通道内流动进行数值模拟研究,分析该转子叶栅的性能及流动特点;然后根据转子叶栅的进口流动参数,设计前排静子叶栅,以实现静转子叶栅叶排间匹配,用以进行超声速压气机静转子级间干涉的数值模拟研究。
研究采用转子叶栅为自主设计叶栅,采用吸力面叠加厚度生成叶型。转子叶栅几何形状如图4,该叶栅叶型为预压缩叶型,叶栅通道为收扩通道,设计来流相对马赫数为1.4,弦长为120 mm,叶栅的进口气流角为60.5°,栅距为70 mm,轮缘速度为415 m/s。此叶栅喉道位于叶型中部,叶型前段采用凹形吸力面设计以实现预压缩,叶型后段弯曲以实现气流转角要求。采用多道斜激波和一道正激波组合增压,抑制每道激波强度,从而降低激波损失,控制叶片表面激波附面层干扰,达到抑制流动分离的目的。

图4 转子叶栅Fig.4 Rotor cascade
在设计点,背压为160 kPa时,转子叶栅的相对马赫数云图如图5所示,在叶栅通道中,气流经过三道斜激波和一道正激波减速增压。由于存在前缘小圆,叶栅前缘将会产生一道脱体激波,其表现形式为一道斜激波和一道向远上游延伸的脱体激波。来流相对马赫数为1.4的气流,在经过叶栅前部预压缩段后,相对马赫数变为1.36;经过第一道斜激波的气流减速增压,马赫数降为1.179;经过第二道斜激波后,相对马赫数降为1.143;第三道激波的强度较弱,经过第三道激波后,马赫数降为1.053;第三道斜激波与结尾正激波相交,增强了结尾正激波的强度,经过结尾正激波后,气流马赫数下降为0.88,正激波后气流保持亚声速流动。

图5 转子叶栅的相对马赫数云图Fig.5 Relative Mach contours for rotor cascade
前缘脱体激波形成的斜激波在叶栅通道传播的过程中发生两次反射,第一次是与叶栅吸力面相交,此时发生马赫反射;第二次发生在叶栅的压力面处,此时激波反射为规则反射。由于每一道反射激波的强度都相对较弱,激波对附面层的扰动较小,再加上采用了平直段设计,两次反射均未造成附面层流动分离。正激波后为扩张段,结尾正激波在压力面附近造成一个小的分离泡,分离泡很快再附。同时,由于结尾正激波处吸力面的物面曲率较大,此时,流动发生分离,附面层较厚且流速较低,甚至很大一部分为亚声速流动,此时在附面层处将无法形成正激波,而是两道曲线激波,曲线激波与结尾正激波交于一点,从而形成一个形如“λ”的波系,其中,第一道曲线激波是由于附面层快速增厚(发生分离)形成,为斜激波弱解;第二道激波可以看作是第一道激波与正激波相交后形成的反射激波,为激波强解。
叶栅的非设计点性能曲线如图6所示,总压损失系数随着增压比先增大后减小,近失速点附近再增加,效率随压比先增大后减小。在近失速点(静压比约为2.25),背压为188 kPa,总压损失系数为0.087,效率为0.916,此时,叶栅脱体激波斜激波与正激波相交,在叶栅唇口处形成“λ”波;在总压损失系数的峰值点(静压比约为1.56),总压损失系数为0.187,效率为0.75;在低压比状态(静压比约力1.43),总压损失系数为0.174,效率为0.727,此时叶栅结尾正激波被推出叶栅通道。
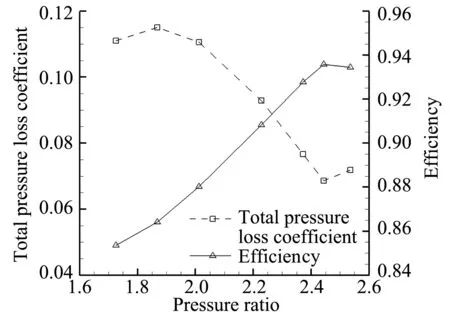
图6 转子叶栅性能曲线Fig.6 Rotor cascade performance
研究采用的静子叶栅为自主设计叶栅,叶型设计采用吸力面叠加厚度的方式生成。该叶栅呈C形,叶栅通道为扩张型通道,设计来流马赫数为0.77,进气角为-27°;出口马赫数为0.64,气流方向为轴向,与转子叶栅进口条件一致。弦长为60 mm,栅距为42 mm。在设计点状态下,马赫数云图如图8所示。由于静子叶栅的吸力面物面为外凸形状,来流在叶栅的吸力面处膨胀加速,将会在吸力面中部附近产生一个局部超声区,结尾于一道强激波。受此激波的影响,吸力面存在一个较小的流动分离区,流动增大了尾迹范围。但总的来说,分离区很小,叶栅损失不大,此设计合理。同时,此分离区的存在,使得静子叶栅存在明显的尾迹区,静转叶栅的干扰更明显,有利于后续研究工作。

图7 静子叶栅Fig.7 Stator cascade
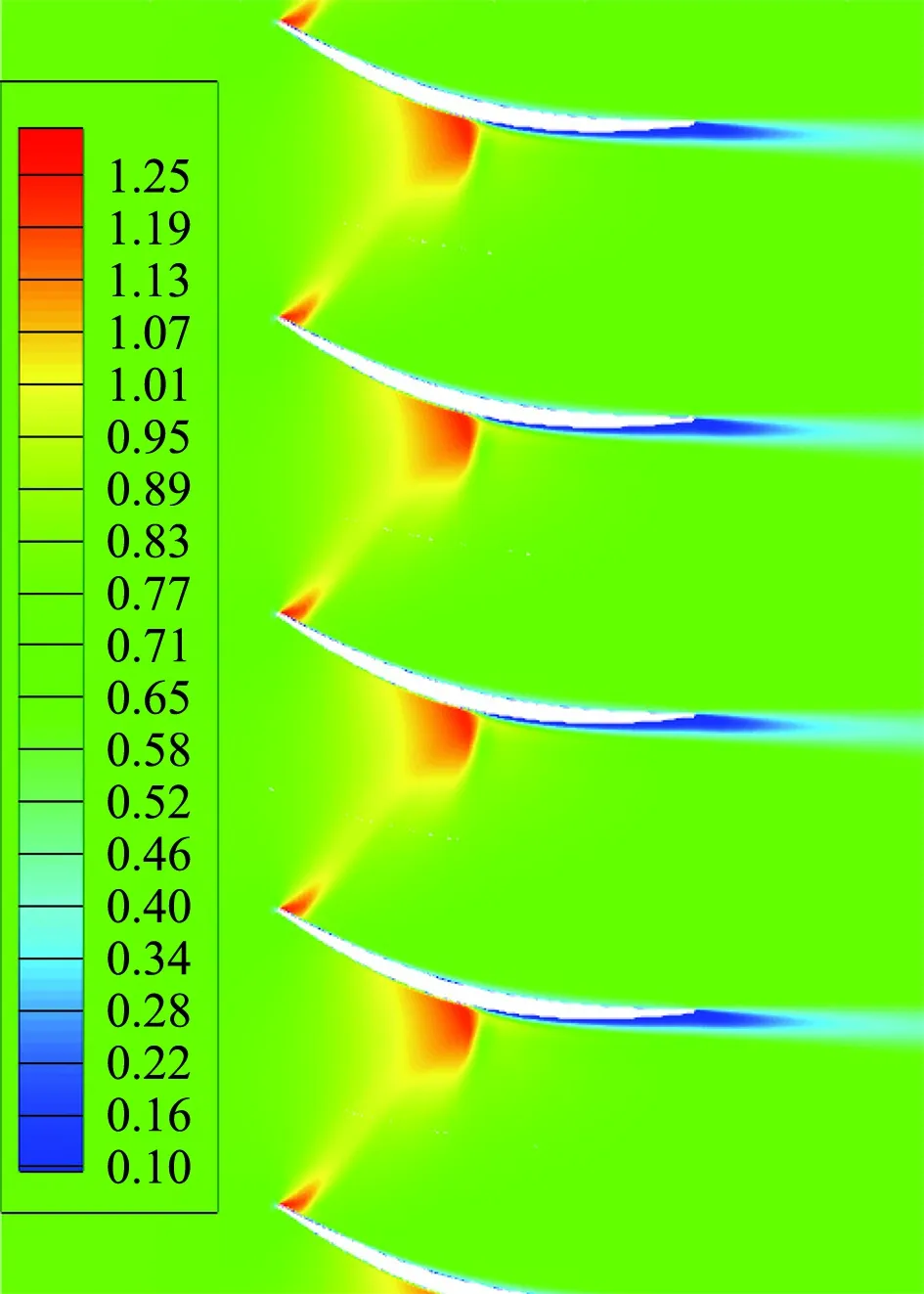
图8 静子叶栅马赫数云图Fig.8 Mach contours for stator cascade
3 静转叶栅间干涉
针对上面的研究结果,计算域的网格生成由Autogrid5自动生成结构网格,静叶和动叶的网格拓扑结构均采用O4H形式,其中静子叶栅单通道的网格数量为4万,转子叶栅单通道的网格数量为6万,叶栅壁面附近的y+值均保持在2以内。
为了节约计算时间和收敛计算步数,本文以基于混合平面法[25-26]定常计算得到的结果作为非定常计算的初场。在使用混合平面法处理静转子交界处时,转子的背压为160 kPa,得到的结果如图9所示,从静压分布云图可知,转子叶栅通道内已建立起相应的激波结构,经过静子叶栅的气流在转子通道中由三道斜激波和一道正激波减速增压后,气流将保持亚声速流动,静压得到较大提升。但由于本文主要是关注静转子级间的干涉情况,此结果仅作为非定常计算时的初场,将不做深入的讨论。
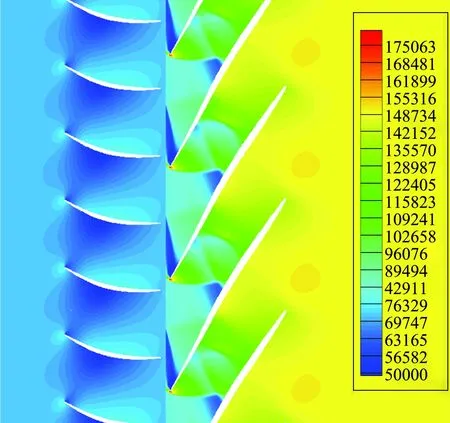
图9 静转叶栅静压云图(混合平面法)Fig.9 Static pressure contours for stator-rotor(mixing plane)
本文根据转子出口处总压的波动进行非定常的收敛判定,在出口压力呈周期性波动以后,URANS数值模拟得到的瞬时静压云图如图10所示。由图可知,在超声速压气机中,转子与上游静子之间存在极为强烈的干涉,使得整个流场表现出强烈的非定常性。

图10 静转叶栅瞬时静压云图(URANS)Fig.10 Instaneous static pressure contours for stator-rotor(URANS)
由于静转子叶栅相对位置的不同,不妨将图中a、b、c处分别看作在一个流动周期内,不同时刻外伸激波与上游静子叶栅干涉的不同表现形式。在a处,转子叶栅前缘产生的脱体激波外伸激波在向上游传播的过程中,接触到上游静子叶片的尾缘,静子叶栅尾缘处尾迹与激波相互干扰,会使得外伸激波发生较小的偏折,经过激波的尾迹流静压升高。
随着静子尾缘和转子前缘之间距离的进一步增大,达到b所示位置。此时向上游延伸的外伸激波被静子叶栅切断。激波在向上游传播的过程中,被上游静子叶栅切割,激波强度逐渐削弱,静子叶栅通道内,靠近叶盆部分的激波强度较大,靠近叶背附近的激波强度较小。不妨采用无黏假设分析,根据激波在介质中的传播规律,激波是以垂直于波面,方向指向图中所示左下,速度大于声速在静子通道中传播的。
随着静转子展向距离的进一步增大,达到c所示位置。此时,由于激波的传播速度大于静子叶栅尾缘附近的气流流动速度,激波在叶栅通道中继续向上游方向传播,同时激波形状发生变化。其主要原因有三:1) 激波不能穿过静子叶栅型面,气流流过激波形成的低速高压区域将会在叶盆附近进一步积累,从而使得叶盆附近低速增压区进一步扩大,而叶背附近的激波则向叶盆运动,在叶盆附近得到积累的低速高压区域得到进一步增大。2) 在静子叶栅通道中,气流在叶背附近膨胀,速度增大,在叶盆附近得到压缩,速度减小,气流速度与激波的速度相互作用,导致叶盆附近激波传播速度较大,而叶背附近传播速度较小,从而造成激波形状发生加大变化。3) 静子叶栅叶盆和叶背处均存在超声区,叶盆处超声区位于叶盆前缘,叶背处超声速位于叶背中部,激波经过较强的超声速区无法继续向上游传播。故而,激波的形状与超声速区的范围有直接的关系。
从图10所示的静压云图不难得出,由于受到下游转子的外伸激波的影响,静子叶栅通道中的流动极为复杂,加大了静转子之间相互干扰的强度,叶栅表面压力表现出强烈的非定常性。
将静子叶片进行编号如图10所示,由于上下边界采用周期性边界条件,满足无限叶栅假设,不同静子叶片表面压力波动可看作一个周期内静压值变化。静子叶片表面压力分布如图11所示,为方便探讨叶片表面压力变化,将5个静子叶片表面压力分布汇总得到图11(f),由图可知,叶片前缘处吸力面和压力面压力扰动最大,这是因为均匀来流在叶栅前缘驻点处分成两股,叶栅前缘半径较小,曲率较大,前缘表面加速度较大,静压迅速下降。分析图11(f)可知,图中stator0表示单排静子叶栅定常计算得到的表面压力分布,压力面压力扰动范围和幅值都比吸力面大。静子叶栅通道内激波在向上游传播的过程中,在吸力面处,对静子叶片38.3%弦长后段静压分布存在影响,且压力扰动幅值呈随叶片弦线先变大后变小的趋势。其中图11(a)叶片尾缘处吸力面压力较大,主要是由于此时转子外伸激波与叶片尾缘相交,激波强度较大,造成叶片尾缘处吸力面压力值跃升较大。在压力面处,对叶片3%弦长后段存在较大影响,且压力扰动幅值随叶片弦向增大,这是因为激波在叶栅通道向上游传播的过程中,激波强度减弱,造成的叶片表面压力扰动也大于叶片前段。

(a) Stator 1

(b) Stator 2
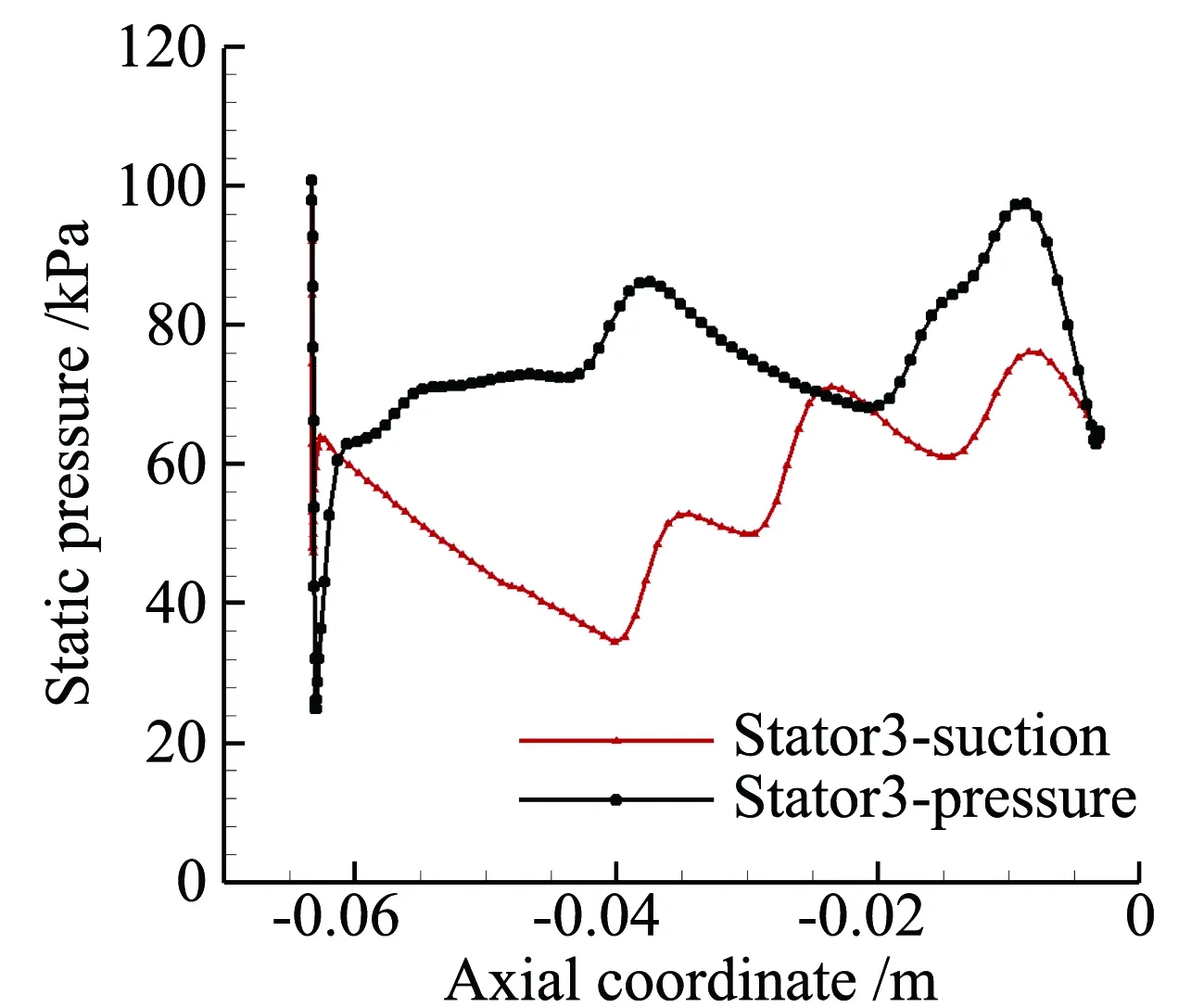
(c) Stator 3
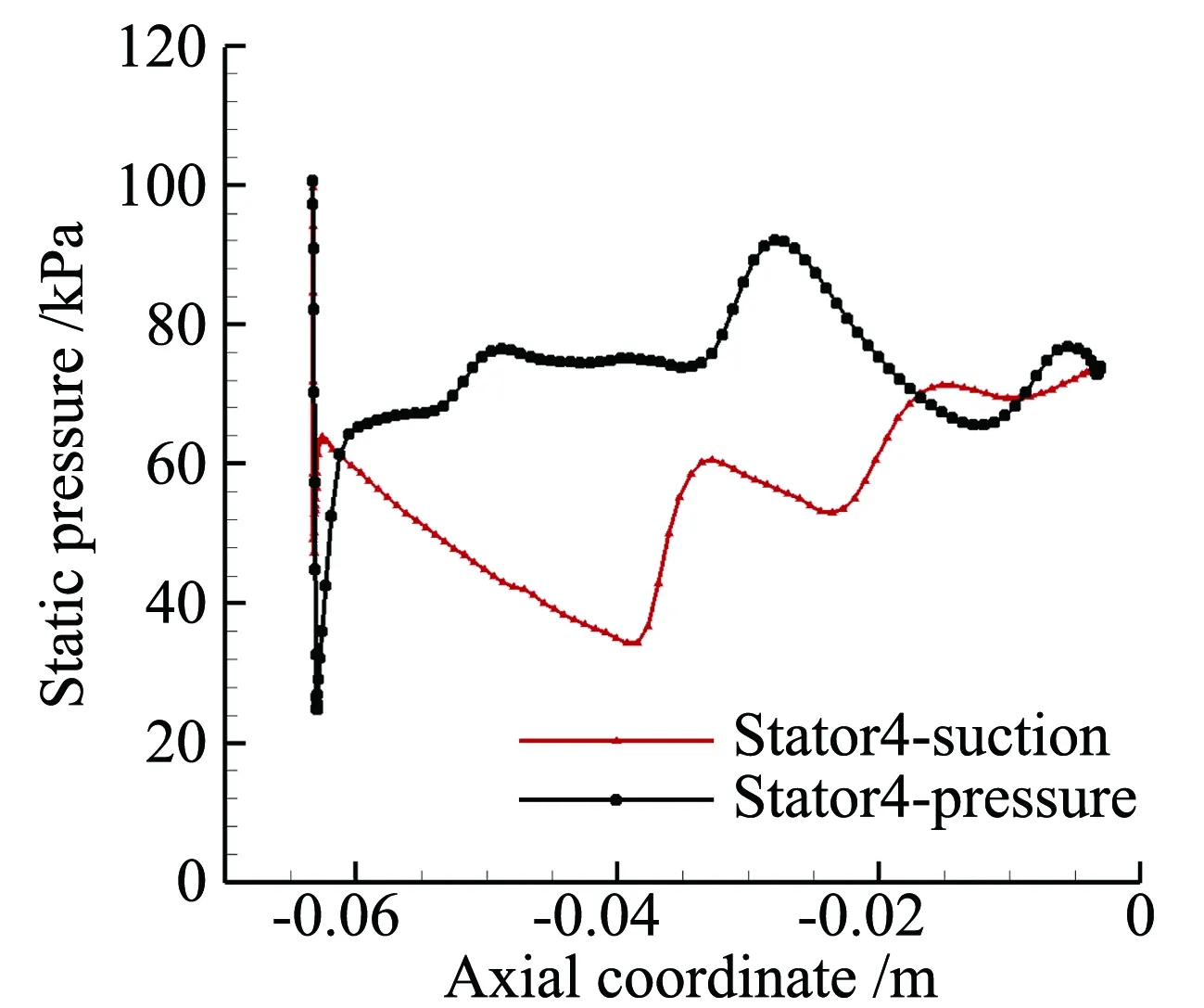
(d) Stator 4

(e) Stator 5
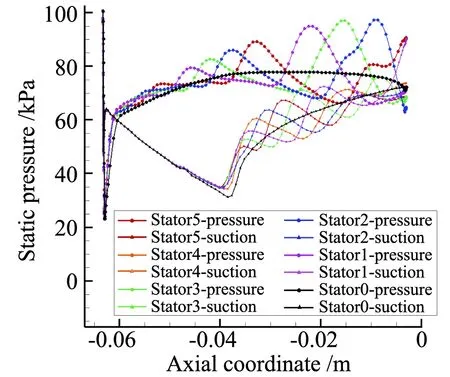
(f) Stators
图12为与上述分析相同时刻的瞬时焓值云图,由此图可以看出,转子叶栅尾迹在向下发展的过程中,出现扭曲、旋转、脱落的迹象,呈类卡门涡街形式脱落。气流经过激波后,焓值增加;同时,叶栅尾迹处,焓值也相对较高,这是因为在尾迹区内,气流的流动速度较低,同时存在一些旋涡运动。
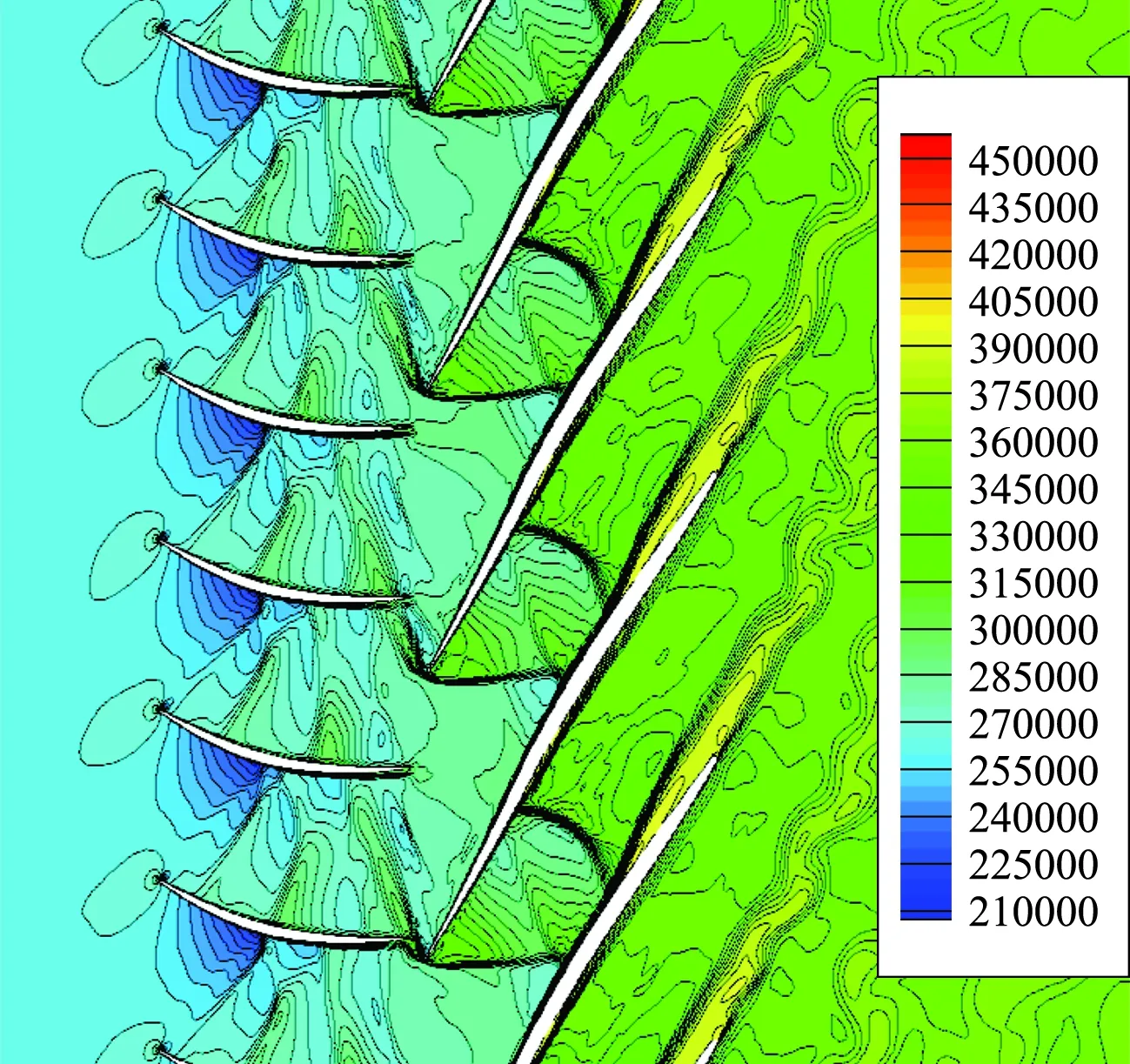
图12 转静叶栅瞬时焓值云图(URANS)Fig.12 Instaneous enthalpy contours for stator-rotor(URANS)
图13为相应时刻的熵值分布图,从图中能够清晰的看出静子叶片尾迹在转子叶栅通道内发展的全过程:上游静子叶栅产生的尾迹在向下游传递的过程中,首先受到转子叶栅的切割。由于尾迹内部存在较为强烈的剪切力,尾迹形成的高熵区被切割后在转子叶片中被输运,同时发生扭曲变形,最后与转子叶片尾迹相互作用,造成如图所示的类卡门涡街运动,引起较大的气动损失。同时,从图中不难看出,被输运的高熵区向转子叶片压力面运动,其主要原因有以下几点:1) 静子叶栅尾迹在向下游传播的过程中存在速度亏损,压力面附近尾迹区速度较小,尾迹在压力面附近得到积累,从而增加了压力面附近尾迹的宽度;2) 由于黏性的影响,在向下游输运的过程中,尾迹与主流势流进一步掺混,使得尾迹区域进一步增大,尾迹损失增加;3) 转子叶栅通道中存在较强的激波,且结尾正激波在压力面附近强度较大,与尾迹相互作用造成尾迹进一步增大。
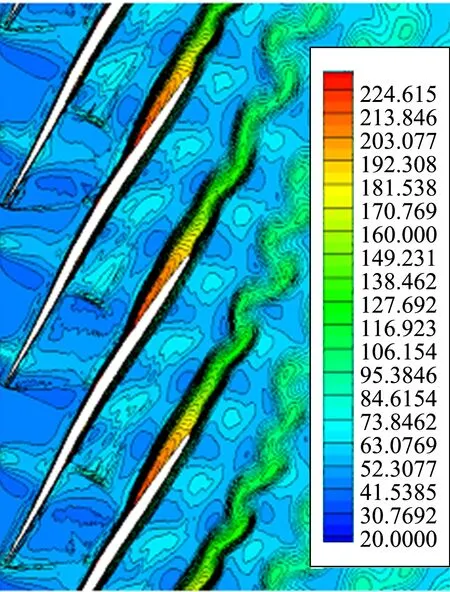
图13 转子叶栅瞬时熵值云图(URANS)Fig.13 Instaneous entropy contours for stator-rotor(URANS)
从图中还可以看出,转子叶栅尾迹呈类卡门涡街的形式向下游摆动,脱落。分析不难得出此现象的形成是上游静子叶栅尾迹带来的低速高熵区域与转子叶栅尾迹相互作用的结果。静子尾迹会诱导转子吸力面产生旋涡运动,同时静子尾迹会与转子尾迹发生掺混,促使转子尾迹发生扭转、变形。但是,静子尾迹对转子叶栅流动并不是都是有害的,合理利用静子尾迹将促进转子叶片表面层流边界层向湍流边界层的转捩,降低激波附面层干扰带来的流动损失,增强叶片表面的抗分离能力;同时,静子尾迹有效促进了转子尾迹与主流势流的掺混,将有利于下游叶排流动的稳定性,提高压气机的稳定裕度。
4 结 论
对内激波转子式超声速压气机静转子叶栅级间干涉的非定常数值模拟研究表明,由于静子叶栅尾迹和转子叶栅栅前激波的存在,转子叶栅通道内存在十分复杂的相互干涉,得到以下结论:
1) 转子叶栅外伸激波在向上游传播的过程中,被静子叶栅切割,并继续在静子叶栅通道中向上游传播,激波形状发生变化,并逐渐向叶栅压力面靠拢,造成叶片表面压力存在较大的扰动。
2) 尾迹内部存在较强的剪切作用,使得其表现出较强的熵增。在向下游流动的过程中,尾迹被转子叶栅切割并输运,与转子叶栅尾迹相互作用,造成转子叶栅尾迹呈类卡门涡街形式脱落。
3) 被切断的尾迹区域在转子叶栅通道中变形并向压力面靠拢,与正激波相互作用后,尾迹区域进一步变大,损失进一步增加。
