高超声速巡航飞行器乘波布局气动设计综述
2018-11-05王江峰王旭东李佳伟杨天鹏李龙飞程克明
王江峰, 王旭东, 李佳伟, 杨天鹏, 李龙飞, 程克明
(南京航空航天大学 航空宇航学院, 江苏 南京 210016)
0 引 言
目前世界各国对临近空间这一空域越来越关注,临近空间的一般定义为地球大气海拔高度20 km至“太空边缘”100 km的高度范围,该高度被称为“Kármán line”(卡门线),开展飞行于该空域的高超声速飞行器研究具有重大的应用价值。对于不同任务形式的吸气式高超声速飞行器,气动布局的设计没有固定可循的模式,但其中的乘波构形由于在高超声速特定飞行条件下(如巡航)特有的优势而被广泛关注,成为吸气式高超声速飞行器一体化布局的重要候选外形。
高超声速飞行器除了高速巡航突防外,在水平起降及可重复使用等方面的要求也越来越高,飞行马赫数范围包括亚、跨、超、高超声速,在进行气动布局设计时必须兼顾低速气动性能。在现阶段工程技术限制下,吸气式高超声速飞行器无法依靠单一动力模式完成水平起降及高超巡航的整个包线过程,而应当使用组合动力系统。高超声速飞行器超燃冲压动力系统的特殊性,要求在气动布局设计中实现机体/推进系统的一体化[1-4]。
对于采用吸气式冲压发动机的飞行器,通过合理的设计激波形状,能够保证进气道入口处流场均匀,从而有效地保证发动机性能。以吸气式超燃冲压发动机为动力的高超声速飞行器的内流道一般由前体/进气道、隔离段、燃烧室、后体/尾喷管组成。由于超燃冲压发动机产生的净推力有限,并且与航空发动机采用压气机进行压缩不同,超燃冲压发动机需要飞行器前体对来流进行压缩,燃烧室产生高温燃气经尾喷管膨胀加速后排出从而产生推力,因此对于吸气式高超声速飞行器而言,机体/推进系统一体化设计就显得尤为重要,尤其是前体/进气道气动布局一体化设计,这对高超声速飞行器的气动布局设计起着绝对关键的作用和影响[1]。
本文针对吸气式高超声速巡航飞行器的气动布局设计技术开展讨论(暂不涉及高超声速领域中的材料、动力、导航与控制、防热等方面),首先对高超声速飞行器发展动态进行了选择性介绍,主要包括超燃冲压发动机的发展历程和主要工业国在高超声速项目方面的发展动态。然后,针对受到世界各国广泛关注的乘波式气动布局高超声速飞行器,从发展状态跟踪与分析出发,对乘波体设计流程、基准流场构建方法、基准流场求解方法、沿展向乘波布局等设计方法进行了详细论述,讨论了不同设计方法的优缺点,对乘波体构型在高超声速气动布局上的应用进行了细致分析。最后,根据本文的分析结果,对高超声速飞行器未来发展进行了展望。
1 高超声速飞行器研究概况
吸气式高超声速飞行器由于动力系统流场与飞行器流场联系紧密,因此对内外流一体化,即机体/推进系统一体化有较高的要求。本节先对国内外高超声速飞行器比较典型的超燃冲压发动机进行简要概述,然后对国外一些具有典型参考意义的高超声速飞行器气动布局设计方案进行讨论,分析了不同设计方案的优缺点。
1.1 超燃冲压发动机
超燃冲压发动机技术是吸气式高超声速飞行器能否实现高效稳定的高超声速飞行且可重复使用的关键,经过近几十年的理论研究、大量的地面试验和飞行演示验证试验,已经证明了超燃冲压发动机的可行性。
超燃冲压发动机大体可分为纯超燃冲压发动机、双模态超燃冲压发动机和双燃烧室超燃冲压发动机。纯超燃冲压发动机是指其只能采用单一超声速燃烧模态的冲压发动机,发动机启动马赫数相对较高,一般在马赫数6以上。亚燃/超燃双模态冲压发动机根据燃烧室内气流速度的不同,分别进行亚声速燃烧和超声速燃烧,因此亚燃/超燃双模态冲压发动机可以工作在比较宽的飞行速度范围内。双燃烧室冲压发动机同时串联了亚燃燃烧室和超燃燃烧室,其工作马赫数范围较小,主要应用于高超声速导弹,如美国HyFly计划中的演示验证飞行器。目前得到广泛研究且应用前景较广的是双模态超燃冲压发动机[1]。
在超燃冲压发动机的可行性得到验证及基础理论得到发展之后,各军事大国都对超燃冲压发动机开展了广泛的研究[2]。美国先后制定了多个高超声速计划,其中多数都是以发展及验证超燃冲压发动机技术为主要目标。通用应用科学实验室(GASL)在20世纪60年代开展了Scramjet Incremental Flight Test Vehicle(IFTV)计划,研制了模型发动机。GASL还进行了一项低速固定几何超燃冲压发动机的研究[3]。NASA于1964年开展了高超声速研究发动机(Hypersonic Research Engine,HRE)计划[4],对超燃冲压发动机进行了风洞实验。之后的NASP计划、HyTech计划、HyperX计划、HyFly计划、SED计划和Falcon计划都对超燃冲压发动机进行了详细的研究,这些将在下一小节介绍美国高超声速一体化飞行器研究概况时介绍。
对于未来发展趋势的可重复使用水平起降的高超声速飞行器而言,其飞行马赫数范围包括亚、跨、超、高超声速,单纯依靠超燃冲压发动机无法实现水平起降。双模态超燃冲压发动机的起始工作下限马赫数是3左右,那么对于起始工作马赫数前就需要其他的动力系统来实现飞行器的起飞与加速。目前解决这一问题的方法是采用组合循环发动机。

图1 并联式TBCCFig.1 Parallel TBCC
组合循环发动机主要分为两类:一类是火箭基组合循环发动机RBCC(Rocket Based Com bined Cycle),另一类是涡轮基组合循环发动机TBCC(Turbine Based Combined Cycle)。对于在大气层内循环飞行的高超声速飞行器来说,采用TBCC推进系统具有更好的经济性能,在飞行的低速段,利用涡轮发动机提供动力,比利用火箭助推产生的比冲大。TBCC推进系统可分为串联式和并联式两大类,串联式TBCC推进系统涡轮/冲压发动机共用进气道、喷管,并联式TBCC(如图1)推进系统涡轮/冲压发动机的进气道、喷管相互独立,通过壁板调节发动机工作模式的变换[5]。涡轮基组合循环(TBCC)发动机可以应用到亚、跨、超、高超声速飞行,其飞行马赫数范围较宽,可以作为水平起降的高超声速飞行器的理想动力装置[6]。鉴于内并联布局形式的TBCC进气道具有适用飞行马赫数范围宽、迎风面积小、内部可用容积率大等优点而具有较大的研究价值和工程应用前景[7]。
1.2 美国
在高超声速飞行器研究领域,美国处于绝对的领先地位。20世纪80年代中期,美国国防部和NASA开展了国家空天飞机(NASP[8-9])计划,NASP计划最终提出了X-30试验飞行器方案。X-30是一架有人驾驶的研究试验飞行器,可以从普通的机场跑道起飞和着陆,能够达到入轨速度(Ma=25),长度在150~200ft之间,起飞总重为250000~300000Ib[10]。NASP计划于1995年被迫中止,为了继续高超声速技术的研究,同年美国空军开展了HyTech(Hypersonic Technology)计划[11]。该计划主要对Ma=4~8范围内碳氢燃料超燃冲压发动机技术开展了深入的研究。
美国NASA继续进行了HyperX计划,在该计划中设计得到了高超声速验证机X-43A[12-13],如图3所示。X-43A采用了升力体布局,前体下部有三道压缩面对来流进行压缩,为超燃冲压发动机提供均匀的气流。尾喷管采用了单壁膨胀式尾喷管。X-43A一共进行了三次飞行试验,第一次飞行试验在2001年6月2日进行,但由于助推器发生了故障,致使试验飞行器偏差正常轨道,最终以失败告终。经过大量的地面试验和计算工作,X-43A最终在2004年3月和11月分别进行了Ma=6.83和9.8的飞行试验,实现了高超声速飞行[14]。

图2 X-30想象图Fig.2 X-30 concept

图3 X-43A气动布局(单位: mm)Fig.3 X-43A configuration(unit: mm)
除此之外,美国海军与国防高级研究计划局(DARPA)开展了HyFly(Hypersonic Flight)计划,即采用双燃烧室冲压发动机推进技术的高超声速吸气式导弹计划[15],该计划源自DARPA前进行的快速响应导弹验证器(ARRMD)项目。

图4 HyFly飞行器Fig.4 HyFly aircraft
HyFly采用轴对称布局形式(图4),动力系统为双燃烧室冲压发动机。在飞行试验中,先由固体火箭发动机助推飞行到Ma=3.5,然后与火箭助推器分离,启动双燃烧室冲压发动机从马赫数3.5加速到6。2008年1月的发射试验就是为了评估双燃烧室冲压发动机的接力性能和加速性能,但超燃冲压发动机并没有按照预定的要求运行[10]。
经过一系列的技术积累和飞行试验,美国在超燃冲压发动机技术领域取得了长足的发展,2005年开始了超燃冲压发动机演示(Scramjet Engine Demonstrator,SED)计划[16],获得了代号为X-51A的超燃冲压发动机乘波体验证机(Scramjet Engine Demonstrator Waverider,SEDWR),如图5所示。虽然X-51A是为了验证超燃冲压发动机,但要使超燃冲压发动机正常工作,需要机体与发动机一体化设计,因此对X-51A气动布局也进行了详细的研究。X-51A采用的是截断型乘波体机身、乘波前体设计,前体下表面具有两级压缩面[17],进气道在弹身腹部,尾喷管为二维机身一体化喷管。X-51A一共进行了四次飞行试验[10],2013年5月最后一次飞行试验中,X-51A成功以5.1倍声速飞行了约3.5 min。
2003年美国空军和国防预研项目局(DARPA)启动了Falcon“猎鹰”计划,图6给出了Falcon计划的发展路线图[18]。Falcon计划最终要实现的是可重复使用高超声速巡航飞行器(Hypersonic Cruise Vehicle,HCV),该飞行器可以从普通的跑道起飞着陆,并以马赫数6.0巡航。Falcon计划中HTV-3X用来演示验证多种高超声速的关键技术,包括高升阻比的气动外形、乘波外形与内转涡轮冲压发动机进气道的一体化设计、轻质可重复使用的高温材料、主动冷却的热管理技术、自动飞行控制、涡轮基组合循环推进技术等[10]。最终HTV-3X和HCV是不依靠推进器并且能够实现水平起降的高超声速飞行器。

图5 X-51A飞行器Fig.5 X-51A aircraft

图6 Falcon计划路线图Fig.6 Falcon series concept
2013年2月,美国洛马公司提出高速打击武器(HSSW)方案[19]。HSSW是一种高超声速导弹概念,可装备未来轰炸机和战斗机,如图7上图所示。但洛马公司在随后再次发表的HSSW效果图中进行了大量修改,具体情况为: 飞行器机体取消了前期上下两条弧形控制曲线拼接设计,转而采用尖顶拱外形; 飞行器控制尾翼从两片水平舵面、两片V型舵面的“Π”型布局改为4片尾翼“X”型布局。此外,随后公布的方案也保留了一些前期设计思路,主要为腹部进气设计和战斗机空射方案,如图7下图所示。
2013年11月洛克希德·马丁公司披露了其SR-72高超声速无人侦察机的研制计划。根据公布的效果图来看,SR-72采用大长细比机身,双腹部进气发动机,大后掠小展弦比梯形翼,前体前缘与主翼前缘错位的直边条,单垂尾。据介绍,SR-72高超声速无人侦察机主要用于取代20世纪70年代研制的SR-71“黑鸟”高速高空侦察机,主要特征为飞行器长30.5 m(小于SR-71的32.73 m),最大航程4300 km左右(与SR-71相同),巡航速度马赫数6(两倍于SR-71的马赫数3)。SR-72飞行器采用与HTV-3X和HCV相同的涡轮基组合循环发动机(TBCC), 分为高速涡轮喷气发动机技术和亚燃/超燃双模态冲压发动机技术,高超涡喷发动机将飞行器加速到马赫数3后,亚燃/超燃双模态冲压发动机点火继续加速至马赫数5到6。从其披露的如图8所示的概念图来看,SR-72也采用了乘波机身以及前体/推进系统的一体化设计。目前高速涡轮喷气发动机为TBCC发动机主要技术难题,SR-72的高速涡喷发动机技术可追溯于SR-71的J-58发动机。双模冲压发动机可能兼具航空喷气洛克达因公司现有技术积累和基本成熟的X-51A发动机技术。


图7 HSSW两种概念图Fig.7 Two HSSW concepts


图8 SR-72外形与动力系统概念图Fig.8 SR-72 concept and dual mode ramjet
1.3 俄罗斯
俄罗斯也已进入高超声速技术的飞行验证阶段,俄罗斯于1991年首次在高空试验中实现了超声速燃烧,这就是“冷”计划[20-21]。“冷”计划试飞器采用的是轴对称的布局[20],如图9所示。该试飞器首次实现了亚燃/超燃双模态冲压发动机从亚燃到超燃的模态转换。


图9 “冷”计划双模态冲压发动机及试飞器Fig.9 “Cold” concept
在进行“冷”计划的同时,另一项“鹰”计划(IGLA计划)也在进行中[22]。IGLA飞行器如图10采用的是升力体构型,长7.9 m,翼展3.6 m,质量2200 kg,头部半径为40 mm,飞行速域范围为马赫数6~14,空域范围为0~80 km,在飞行器机体下方有3台超燃冲压发动机。


图10 IGLA飞行器Fig.10 IGLA concept

图11 彩虹-D2飞行器Fig.11 Rainbaw-D2 aircraft
俄罗斯还进行了“彩虹D2”计划[23]和“鹰31”计划[24]。图11为俄罗斯在1997年航展上展示的高超声速试验飞行器。
1.4 欧洲
1992年法国启动了PREPHA计划。在该计划中,提出了通用单级入轨SSTO飞行器的设计方案及其推进系统,如图12(a)[25]。该飞行器推进系统采用了四种组合循环推进系统:双通道的涡轮火箭超燃冲压火箭组合与涡轮喷气双模态超燃冲压发动机火箭组合,以及单通道的火箭双模态超燃冲压发动机火箭组合与引射双模态超燃冲压发动机火箭组合[10]。该飞行器所考虑的飞行任务为从航天发射场起飞到达倾角28.5°的500 km圆轨道,在这样的任务条件下,飞行器长度为65 m,翼展37.5 m,机翼表面面积306 m2,进气道进口截面面积为24 m2,起飞质量为476 t。

(a) PREPHA计划飞行器

(b) JAPHAR计划飞行器
与此同时,德国开展了名为Sanger计划的两级入轨航天运载器的概念设计研究[26-27]。Sanger方案将整个系统分为两级,第一级是运载器,第二级是轨道飞行器,轨道飞行器背驮在运载器背部。第一级运载器采用涡轮冲压组合循环发动机,Sanger在常规机场水平起飞,所需跑道长度为2500 m,飞行到31 km的高空后,飞行速度达到Ma=7,然后轨道飞行器与运载器分离,运载器返回机场水平着陆,轨道飞行器依靠自身的火箭发动机进入地球轨道。
在法国PREPHA计划和德国Sanger计划结束后,两国研究人员联合开展了JAPHAR(Joint Airbreathing Propulsion for Hypersonic Application Research)计划[28],JAPHAR飞行器如图12(b)[29]。JAPHAR计划的第一个目标是进一步发展双模态超燃冲压发动机技术,深入研究工作机理,提高数值模拟的计算精度。第二个目标是研究机身/发动机一体化情况下的推力与阻力平衡问题。

图13 德国Sanger飞行器想象图Fig.13 Germany Sanger concept
1.5 日本
日本高超声速飞行器及重复使用航天飞行器技术[30-31]始于20世纪80年代,计划完成新一代高超声速飞行器和可重量使用的轨道飞行器。日本计划发展采用吸气式发动机与火箭组合的单级入轨飞行器,以及采用TBCC动力的第一级和采用火箭动力的第二级的两级入轨飞行器,第一级携带第二级加速到马赫数6.0后进行分离,第二级依靠火箭动力进入轨道[32]。


图14 日本单级及两级入轨高超声速飞行器方案Fig.14 Japan SSTO and TSTO concept
从上述研究概况分析可以看到,在吸气式高超声速飞行器技术方面,推进系统的研究仍然是重中之重。而且对于吸气式高超声速飞行器而言,推进系统不再是一个独立的系统,而是必须要和飞行器机体进行一体化设计,这也是为什么在吸气式高超声速飞行器研究中必须关注机体/推进一体化的原因所在,其核心工作是在满足推进系统工作的条件下,必须保证飞行器总体气动特性。
吸气式高超声速飞行器总体气动布局形式是与飞行器的任务与用途相联系的,因此在气动布局形式上不能统一而论,气动布局设计方法也不相同。近年来随着人们对高超声速飞行器任务需求的不断提高,乘波式布局以其特有的优异性能引起了研究者的高度重视,下面本文就对这种气动布局设计方法进行讨论。
2 高超声速乘波飞行器设计方法
2.1 乘波前体/进气道设计方法
对于高超声速飞行器,前体作为压缩面对来流减速增压,对进气道的性能起到决定性的作用。乘波体由于其优异的性能和对来流的压缩作用,是吸气式高超声速飞行器比较理想的前体/进气道气动布局方案[33-34]。Nonweiler[35]在1959年首先提出了“乘波”的概念,Nonweiler利用二维楔流场生成了具有“∧”形横截面的乘波构型,如图15(a)。1980年,美国马里兰大学的Rasmussen[36-38]等提出了由圆锥绕流流场生成乘波构型的方法。1990年,Sobieczky[41-43]提出了吻切锥法生成乘波构型。1966年,Mölder[44]首次提出将Busemann内锥形流场用于高超声速进气道设计的概念。

(a) “∧” 形乘波体

(b) 锥导乘波体

(c) 吻切锥乘波体
理想状态的乘波体是在超声速或高超声速飞行器时,前缘全部贴附在激波曲面上且将流场完全分割成为互相无干扰的两部分的一种特殊气动构型,这也是“乘波”名称的由来。乘波体的特性决定了在越接近理想设计状态下越能减少乘波体下表面高压压缩区向上表面自由来流或低压区的溢流,相同迎风面积下最大程度地提升来流捕获流量。相对于常规升力体,贴体的前缘激波和较少的溢流也就决定了乘波体有更好的来流预压缩性能,更大的升阻比特性。无论是高超声速前体还是高超声速进气道,只要满足乘波体的定义,都属于乘波体设计范畴,在高超声速飞行器气动布局中,两者除传统功能性区别,在设计方法上基本一致且越来越趋向于一体化设计,在这里就不分别讨论了。
乘波体最初的传统设计方法为:给定生成体,在设计的飞行条件下求得生成体生成的基准流场,一般为类锥形基准流场;选取一个指定形状的柱面作为流动捕获管(Flow Capture Tube,FCT)与类锥形激波面相交,得到乘波体的前缘,离散前缘曲线分别在类锥形基准流场中进行流线追踪;将各条流线连接成曲面并且上表面取自由流面或者非脱体激波压缩(膨胀)面,即得乘波体构型。
经过多年发展,现在普遍采用的乘波体设计方法及流程为:在给定的来流马赫数及飞行条件下,根据性能需求预先设定流动捕获曲线(Flow Capture Curve,FCC)和进气道进口曲线(Inlet Capture Curve,ICC),FCC曲线和ICC曲线可以是任意形状,但是要保证ICC曲线上点的曲率连续;借用微分思想将给定的ICC曲线离散成多段小圆弧,而每段小圆弧为类锥形激波与底部截面(或唇口截面)相交的部分,每段小圆弧分别对应一个类锥形绕流,ICC曲线相应离散点的曲率半径线与FCC曲线的交点为与该点对应的乘波体前缘点在底部截面的投影点,由此构建一个吻切平面;在每个吻切平面内构建基准流场,根据前缘投影点坐标求出在前缘激波面上真实坐标并在基准流场中进行流线追踪;将各条流线连接成曲面并且上表面取自由流面或者非脱体激波压缩(膨胀)面,即得乘波体构型。这两种设计流程的主要区别在于沿展向乘波体设计方法上的不同,详细论述将在后面章节展开。
根据设计流程中的具体特征,乘波体设计方法大致可以归纳为沿来流纵向基准流场的构建方法、沿来流纵向基准流场的求解方法、垂直来流展向的乘波体设计方法及乘波体在高超声速气动布局中的拓展应用等几个方面。下面就针对这几个方面进行较为细致的讨论。
2.2 基准流场的构建
用于追踪乘波体型面流线的无黏(一般情况下为无黏)超声速或者高超声速流场称为乘波体(或者乘波体吻切面)的基准流场,这里无黏的基准流场与无黏的乘波体流场是两种截然不同的概念。一般情况下生成基准流场的几何体称为基准流场的生成体。根据生成体的几何构型,基准流场可以分为二维平面基准流场、三维非轴对称基准流场以及三维轴对称基准流场。其中三维轴对称基准流场包含纯三维轴对称基准流场以及每个吻切面内等效的三维轴对称基准流场。某种程度上来说,基于纯三维轴对称基准流场的锥导乘波体或者类锥导乘波体是基于吻切理论乘波体的一种特例,即ICC曲线曲率半径保持恒定,为圆弧曲线。
根据基准流场的生成条件,基准流场可以分为生成体物面几何参数可控的基准流场、生成体物面压强参数可控的基准流场、生成体物面马赫数可控的基准流场、前缘激波可控的基准流场以及以上多参数组合可控的基准流场。
2.2.1 物面几何参数可控的基准流场
物面几何参数可控的基准流场即生成体几何参数已知,直接求解生成体无黏流场作为基准流场,进而进行流线追踪生成乘波体构型。乘波体最开始被关注和研究就是从此类基准流场开始,根据生成体的几何构型,基准流场基本分为二维平面基准流场、三维非轴对称基准流场以及三维轴对称基准流场等。
2.2.2 二维平面基准流场
Nonweiler[35]在1959年首先提出了“乘波”的概念,利用二维楔流场生成了具有“∧”形横截面的乘波构型,也称为楔导乘波体,如图15(a)所示。
另外还存在典型的二元进气道,其对来流的压缩是通过多个预压缩楔面实现的,如图16所示[45]。二元进气道结构简单,各楔面的压缩相当于二维平面压缩,流场便于计算与分析,因此国内外对二元进气道的研究也比较多[46-48]。二元进气道的设计一般采用多级楔面对来流进行压缩,并且在设计状态多级楔面产生的多道斜激波交汇在进气道唇口[49],进气道的外罩与最后级楔面构成二元进气道的内压缩段,对气流进行进一步的压缩,两侧为进气道的侧壁,一起构成了矩形的进气道出口。美国X-43A、X-51A飞行演示验证飞行器就是采用的典型的二元进气道[50-51],当然这两种飞行器的二元进气道并非严格意义上的乘波体。由二元进气道的概念可以看到,这种进气道具有溢流严重、构型单一等方面的不足。
在二元进气道的基础上拓展的三维侧压进气道(图17[52])在纵向截面内与二元进气道相同,但是增加了二元进气道竖直侧壁方向二维侧板的向内压缩。三维侧压式进气道具有固定的几何形状、较低的来流边界层敏感度、较短的压缩通道、较低的启动马赫数、较小的外阻等特点。Trexler[53-54]最早提出三维侧压式进气道的概念,并通过理论分析和试验验证研究了侧板收缩比和侧板后掠对起动性能的影响,得出了增大侧板收缩比不利于进气道起动、侧板后掠有助于进气道起动的结论[55]。之后Holland为研究影响侧压式进气道起动相关因素,对侧压式进气道进行了大量深入的数值与试验验证[56-61],确定侧板压缩角是十分关键的参数,并定量给出侧压式进气道的侧板压缩角的取值为6°左右[62-64]。国内,张堃元[65]较早地开展了相应的三维侧压式进气道的设计方法研究,分析了侧板压缩角、前缘后掠角以及唇口位置等参数对进气道性能的影响。虽然二元进气道及三维侧压式进气道并非严格意义乘波体,但对乘波体的研究有参考指导意义。

图16 二元进气道示意图(单位: mm)Fig.16 2D inlet(unit: mm)


图17 三维侧压式进气道Fig.17 3D sidewall compression inlet
2.2.2.1 三维轴对称基准流场
三维轴对称流场分为轴对称直外锥绕流、轴对称曲外锥绕流、轴对称内直锥绕流、轴对称曲内锥绕流等。
1968,Jones[66]首次将高超声速迎角0°圆锥绕流作为基准流场进行乘波体设计,生成的乘波体称即称为锥导乘波体,锥导乘波体基准流场的生成体为母线为直线的轴对称圆锥,Jones的锥导乘波体设计方法对乘波体布局的设计研究有标志性指导意义。
1988年,Corda[67]等进行了基于一般性轴对称基准流场并且考虑了黏性作用的乘波体构型设计及优化的方法研究。文章中基准流场的生成体不仅采用了母线为直线的圆锥,而且采用了母线分别为3/4和1/2幂次曲线的曲圆锥,其基准流场的求解采用了空间推进的有限差分方法。该基准流场的构建方法对最大升阻比或者最小阻力乘波体构型设计提供了一定的新思路。


图18 冯卡门曲线及其基准流场Fig.18 Von Karman ogive and generating flowfield
2006年,Mangin[68]等同样进行了基于幂次曲线生成体的轴对称基准流场的乘波体构型优化设计,不同于Corda的是,Mangin采用的是钝头体幂次回转体,钝头体基准流场因为有脱体激波存在需要CFD方法进行求解。2015年丁峰[69]等在Corda、Mangin等基础上提出了一种基于特征线法的乘波体构型设计方法,首次采用冯卡门曲线(Von Karman ogive)作为轴对称基准流场生成体母线,并对钝头体冯卡门曲线进行了近似尖锥处理以便能使用特征线方法进行流场求解,如图18所示。该方法最终流线追踪出的乘波体构型某种程度上继承了冯卡门回转体的气动特性,具有较大的升阻比和容积率。
1956年,Connors和Meyer[70]提出了一种适用于二维和三维轴对称超声速进气道的设计方法。该方法主要构造了一种二维和三维轴对称曲面锥流场,曲面锥母线包括直线段和等熵压缩段,其中直线压缩段为流场前缘激波依赖区,直线段末端处马赫线与前缘激波交点为等熵压缩段的流场焦点并且该马赫线作为等熵压缩区起始马赫线,在焦点处假设为二维逆Prandtl-Mayer流动关系式,利用轴对称势流特征线法计算这一等熵流场,如图19所示。2006年,耿永兵[71]在此基础上以升阻比为优化目标,在来流马赫数2~4及飞行高度20~24 km条件下,进行了轴对称近似等熵压缩流场的乘波前体优化设计,结论表明近似等熵压缩下表面的乘波前体在设计条件下具有良好的气流压缩效果。

图19 直线段+等熵压缩段流场Fig.19 Flowfield of cone and isentropic compression
2009年,贺旭照[72-73]等将Connors提出的直线段+等熵压缩段流场改进为如图20所示的直线段+等熵压缩段+直线段的基准流场,并利用吻切理论生成了密切曲面锥乘波前体,与密切锥乘波体的比较结果表明,密切曲面锥乘波体克服了密切锥乘波体压缩量不足及容积率偏小的缺点。

图20 直线段+等熵压缩段+直线段流场Fig.20 Flowfield of cone +isentropic compression + cone
1967年,Mölder[74]提出并总结了4种基于Taylor-Maccoll方程求解的三维轴对称流场,分别为:三维绕圆锥外流场、Busemann内锥形流场、内锥形流场A (Internal conical flow A)、内锥形流场B (Internal conical flow A),如图21,虽然Mölder提出这4种流场时并没有将其应用于乘波体设计,但是对后来众多学者在乘波体基准流场构建工作上提供了很大的向导作用,如前文Jones提出的绕圆锥外流场的乘波体设计方法。

图21 Molder提出的4种三维轴对称流场Fig.21 Flowfields of four types of axisymmetric cones
2000年,Goonko[76]等提出了基于内锥形基准流场的乘波前体设计方法,该方法中基准流场生成体为形状类似“喇叭”的三维轴对称内锥管,内锥管型面母线为带有一定内倾角的直线,如图22所示,基准流场前缘激波贴附于内锥管前缘并相交于内锥管轴线处。Goonko将内锥乘波体与基于二维楔形斜激波流场和三维轴对称外锥形基准流场的乘波体进行了对比,因为内锥形基准流场内收缩的特性,内锥管物面压强不继上升,因此继承了基准流场特性的内锥乘波体有更大的升力系数和更强的来流预压缩能力;同时计算结果表明内锥乘波体相比于外锥乘波体沿展向压力系数、升力系数、升阻比变化较为平缓,流场较为均匀,但是沿展向热流系数变化趋势相反。Coonko同时指出影响该类乘波体气动参数的主要因素是流动捕获曲线的起始追踪纵向位置,影响热流系数的因素是流动捕获曲线在横截面上的曲率半径大小。

图22 内锥乘波体示意Fig.22 Inner cone waverider outline
国内学者也对该类乘波体进行过相关研究,2006年,尤延铖[77-78]等在该方法的基础上进行了内乘波式进气道的研究,研究结果显示黏性对该类乘波体进气道有较大影响,内乘波式进气道各项气动参数高于典型的二维侧压式进气道。2011年,贺旭照[78]等在Coonko方法的基础上进行了拓展,Coonko方法中直内锥型面实际前缘激波是下凹的,而直前缘激波的内锥型面实际是上凸的,贺旭照采用了Mölder提出的ICFA流场作为内锥形乘波体设计的基准流场,并利用吻切理论在每个吻切面对基准流场进行缩放来拓宽FCC和ICC的给定条件,设计得到的乘波体称为密切内锥乘波体。

图23 各种截短Busemann进气道Fig.23 Several truncated Busemann inlets
Busemann内锥形进气道包含了一系列的等熵压缩马赫波和末端激波,末端激波将气流重新转向沿轴向流动,并且这些马赫波和末端激波都交于一点。1966年,Mölder[44]等首次将内锥形流用于三维轴对称Busemann进气道的设计。1992年,Billig[80-81]等人将流线追踪技术引入到Busemann进气道的设计中,得到了流线追踪Busemann进气道。流线追踪Busemann进气道的设计流程为在基准Busemann进气道入口截面内取一段封闭曲线,将该曲线分为若干个点,从每一个点出发在基准Busemann进气道流场内流线追踪直到进气道出口。流线追踪Busemann进气道相比于基准Busemann进气道,设计方法更加灵活实用,解决了基准Busemann进气道长度过长的缺点,根据封闭曲线的不同,可以设计得到不同形状的流线追踪Busemann进气道。基准Busemann进气道以及流线追踪Busemann进气道都是在无黏条件下进行的,在黏性条件下,边界层的存在相当于增加了壁面的厚度,造成马赫波聚合点前移和并且聚合效果不好[82]。Van Wie[83]等提出了通过边界层位移厚度对Busemann进气道进行修正的方法,修正后的Busemann进气道的流场能够较好的符合无黏设计条件下的流场。另一方面,截断Busemann进气道是提高其黏性条件下性能的一个有效方法,孙波[84]等对截短流线跟踪Busemann进气道进行了研究。
2.2.2.2 三维非轴对称基准流场
众多学者不仅对基于三维轴对称基准流场的乘波体设计方法进行了大量的研究工作,而且也对基于三维非轴对称基准流场的乘波体设计方法也进行了研究拓展。
1979年,Rasmussen[85-86]首次将三维非轴对称基准流场应用于乘波前体的设计,通过高超声速小扰动理论构建了小迎角圆锥绕流、小迎角椭圆锥绕流和零迎角椭圆锥绕流三种基准流场。因为流场的求解基于高超声速小扰动理论,基准流场是在轴对称锥形流场的基础上由迎角和横截面偏心率的小扰动形成的,所以基准流场也是类锥形的。Rasmussen设计的乘波体FCC曲线为经过基准流场锥点的直线,因此生成乘波体也是类锥形的,称之为锥形乘波体。同时Rasmussen给出了来流马赫数、特征锥顶角、小扰动来流迎角及横截面偏心率对乘波体形状、压力分布和激波结构的影响规律,并在乘波体的自由来流上表面应用了经过缩放的非对称楔导乘波体来进行乘波体的偏航控制。随后Rasmussen[87]和Jischke[88]对该类乘波体进行了来流马赫数3~5、迎角及侧滑角±20°内、单位雷诺数2×106/ft条件下气动力、气动力矩及物面压力系数分布的试验研究,结果表明基于锥形流动假设的一阶小扰动理论能够满足乘波体构型的精确设计,并且非设计状态下气动参数与设计状态下气动参数变化较为光顺,流场中无非设计状态强激波出现。随后Lin[89]在Rasmussen基础上拓展了基于小扰动椭圆锥基准流场的乘波体设计方法,不仅加入了横截面偏心率的小扰动,而且考虑了纵向母线偏心率的小扰动,使得乘波体基准流场的生成体由三维轴对称直圆锥变成具有横向椭圆型线和纵向部分椭圆母线的三维非轴对称类锥体。之后Lin和Luo[90]考虑了进气道型线的流线追踪,进行了前体/进气道的一体化设计,并对黏性影响进行了计算分析。2006年,乐贵高[91]等采用三阶MUSCL型TVD格式的N-S方程计算了椭圆锥演化的乘波体高超声速流动问题,分析了该类乘波体各项气动参数的变化规律,并与实验数据进行了对比。同年,崔凯[92]等同样采用CFD方法在马赫数6、迎角0°和30 km飞行高度的设计条件下,综合分析了23种源自不同锥体流场所获乘波体的性能,结果表明当基本锥体为椭圆锥,且截面椭圆宽高比在1.5~1.618时,所获得的乘波体具有最大的升阻比;而当截面椭圆宽高比约为1∶1.5时,所获得乘波体阻力最小。
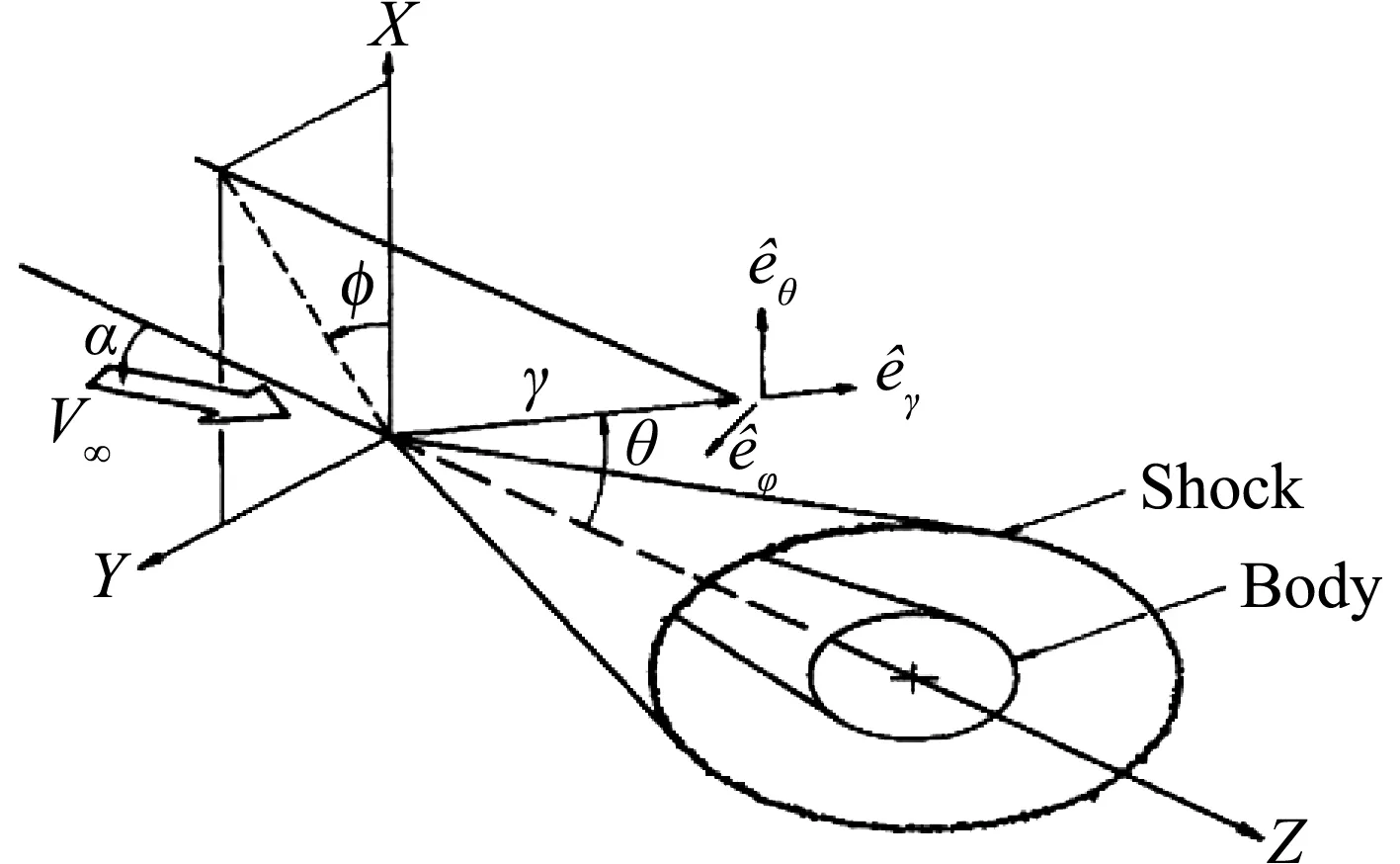
图24 椭圆锥乘波体生成体Fig.24 Flowfield derived elliptical cone
1994年,Takashima[93-94]等为了得到比轴对称基准流场更均匀的进气道流场,提出了使用非对称基准流场设计进气更均匀的乘波体设计方法,即使用楔锥组合体作为生成体的楔锥乘波体设计方法。随后与锥导乘波体和吻切锥乘波体的对比显示,楔锥乘波体有更大的容积率和更均匀的进气道流场,但是因为楔锥乘波体基准流场的求解基于CFD方法,楔锥乘波体激波的精确捕捉和气动参数的优化受到了限制。2003年,刘嘉[95]和王发民[96]等提出了用相交楔锥流场构造乘波构型飞行器前体的方法,该方法利用无黏相交楔锥流场生成具有两个压缩面的乘波前体,不仅兼具楔型流场和锥型流场构造乘波体的优点,而且充分发挥了高超声速飞行器前体的预压缩作用,为进气道的正常工作提供了条件。2013年,明承东[97]利用楔锥乘波体设计方法进行了前体/进气道的一体化设计。

图25 楔锥乘波体基准流场生成体Fig.25 Flowfield derived wedge-cone
2.2.3 物面压强参数可控的基准流场
2011年,南向军[98-99]提出了压升规律可控的高超声速内收缩进气道设计方法,如图26所示。该方法基于由旋特征线理论选取物面压升规律给定的三维轴对称流场作为乘波进气道设计的基准流场。南向军对三种不同压升规律的内收缩进气道性能进行了比较,分别为等压力梯度物面、二次曲线压力梯度增大物面、二次曲线压力梯度减小物面的三种进气道,结果表明流线追踪的进气道物面能够较好的保持基准流场给定的压升规律,压力梯度增大的进气道压缩效率最高,其次为等压力梯度,压力梯度减小的进气道压缩效率最低,同时压升规律的可控也对乘波体整机的力矩配平有较大的益处。南向军也进行反正切压升规律可控的内收缩进气道的研究。此后向有志[100]在该方法的基础上结合替代模型多目标优化设计了一种高超声速轴对称进气道,并与常规双锥和三锥轴对称进气道进行了比较,结果显示压升规律可控的三维轴对称进气道在起动点的流量系数和总压恢复系数比双锥和三锥轴对称进气道得到了提高。


图26 轴对称压升规律可控基准流场Fig.26 Flowfield derived from controlled pressure
2017年,何家祥[101]等提出了基于Busemann压升规律可控的消波内转基准流场设计方法,该方法的大致流程为,计算给定条件下经典Busemann进气道物面压力参数并进行五次多项式压力参数的近似拟合,经典Busemann进气道前段物面压力参数变化较平缓,因此仅采用中后段拟合的压升规律作为截短的Busemann压升规律进行基准流场的构建,设计的进气道继承了经典Busemann进气道高效的压缩特性,但是在长度上有效减短。
2.2.4 物面马赫数可控的基准流场
2012年,李永洲[102]在壁面压升规律可控的乘波前体/进气道设计方法基础上,受到超声速管道设计中等马赫数分布规律的启发,加之进气道设计中对出口马赫数有一定要求以满足燃烧室需要,提出了一种给定壁面马赫数分布规律来设计基准流场的新方法。该方法对几种典型的马赫数分布规律基准流场进行了对比研究,分别为截短基准Busemann流场、线性变化的等马赫数梯度基准流场、二次曲线马赫数梯度增加基准流场、对数变化的马赫数梯度减小基准流场和反正切马赫数分布规律基准流场,如图27所示。对应的物面压力分布显示,等马赫数梯度基准流场近似于截短Busemann基准流场,压力分布规律与马赫数分布规律基本呈负相关特性。该方法拓展了基准流场的选择范围,随后,李永洲在该方法的基础上进行了方转圆内收缩进气道的设计及试验验证以及基准流场灵敏度的分析与优化设计。


图27 5种基准流场壁面处马赫数分布规律及压升规律Fig.27 Mach distributions and derived pressures for five baseline flowfields
2.2.5 激波参数可控的基准流场
1990年,Sobieczky[41]提出了一种基于给定激波形状逆向求解基准流场的乘波体设计方法,该方法中任意形状的三维激波可以做为激波后流场推进求解的初值,乘波体前缘点在求解基准流场的同时进行了流线追踪,该方法结合吻切理论不仅可以生成圆锥形前缘激波的基准流场,而且可以生成任意给定ICC曲线的三维类锥形前缘激波的基准流场。随后Jones[103-104]在Sobieczky基础上对该方法进行了深入细致的研究,通过改变FCC曲线与ICC曲线进行了大量算例的验证与比较,并针对给定计算条件进行了基准流场的构建并设计了乘波前体布局,如图28所示,说明了该方法在乘波前体布局设计上较为适用。

图28 吻切锥方法示意及激波可控的基准流场和乘波前体Fig.28 Osculating waverider based on controlled shock
1996年,钱翼稷[105]使用该方法进行了乘波体设计技术研究,发展了一种轴对称流的逆特征线法,即从一道给定的激波波后的初值线出发,向“物面”推进求解,这与常规的沿物面向下游推进求解的作法不同,称其为逆特征线法。这就相当于定义了一条初值线(非特征线),可以在激波后的依赖区内求解Cauchy问题,并沿与主流相垂直的方向推进求解,这是一种求解物面流线的反设计方法。此后薛倩[106]、肖洪[107]、乔文友[108]等都在逆特征线方法的基础上进行了基于给定激波的多级基准流场构建并进行了乘波前体及进气道的设计研究。
2.2.6 多参数组合可控的基准流场
多参数组合可控的基准流场即上文中提到的多种参数组合可控的基准流场。2009年,肖洪[107]设计了如图29所示的能够产生三道封闭圆锥激波的相交锥基准流场,其中第一级激波及波后流场由Taylor-Maccoll方程求解,第二、三道直激波及波后流场由特征线方法求解,该基准流场可归类为多级激波可控的基准流场。

图29 三级封闭激波基准流场Fig.29 Flowfield derived three intersecting shocks

图30 前缘激波+压升规律可控基准流场Fig.30 Flowfield derived from controlled shock and pressure
2012年,卫峰[109]利用三维轴对称内锥形基准流场进行乘波前体/进气道的一体化设计,如图30所示,其中基准流场前缘激波指定为直激波,通过有旋特征线法求得前缘激波依赖区后,给定物面压升规律,以前缘激波依赖区末端马赫线为初值线计算给定压升规律压缩区的流场,随后给定进气道入口反射激波参数捕捉反射激波位置并进行内转向消波设计。该流场可归类为激波参数+压升规律组合可控的基准流场。
2014年,贺旭照[72-73]等利用吻切理论生成了密切曲面锥乘波前体,该方法中每个吻切面基准流场由给定前缘直激波及激波依赖区+等熵压缩压+直壁面自由流区构成,因此基准流场物面由直线段+等熵压缩段+直线段构成,如图20所示,该方法中流场可归类为激波参数+物面几何参数(等熵压缩条件)组合可控的基准流场。

图31 马赫数+压升规律组合可控原理图Fig.31 Compression wall with controlled Mach and pressure
2017年,张林[110]采用压力/马赫数复合分布规律的弯曲压缩面生成基准流场进行了二维进气道的设计研究工作,如图31所示。该方法流场可归类为物面马赫数+压升规律组合可控的基准流场。同年,王丁[111]研究分析了基准流场主压缩区物面压升规律对基准流场性能的影响,如图32,提出了一种双曲正切压升规律。研究表明,在增压比大致相同的条件下,与直线压升规律和二次曲线压升规律相比,双曲正切压升规律具有较好的压缩效率及起动性能。该方法流场可归类为前缘激波+压升规律组合可控的基准流场。

图32 激波+压升规律组合可控原理图Fig.32 Compression wall with controlled shock and pressure
2016年,丁峰[112]研究分析了物面压升规律对乘波前体气动性能的影响,方法中乘波体基准流场由前缘直激波依赖区和给定压升规律压缩区构成,如图33所示。该研究给定的三种压升规律分别为等压力规律、压力递增变化规律和压力递减变化规律,并对比分析了三种乘波体容积率及气动参数的区别。该方法流场可归类为激波参数+压升规律组合可控的基准流场。
近些年,越来越多的国内外学者对基于多种参数组合可控基准流场的乘波体设计方法进行了研究,这里就不一一枚举了。
由上述分析,在基准流场构建方面,可以总结为

图33 前缘激波+压升规律组合可控原理图Fig.33 Compression wall with controlled shock & pressure
以下几个方面:
1) 基准流场的生成体物面几何参数可控相当于将生成体几何参数做为基准流场的可调整设计参数,追踪拟合的乘波面基本继承生成体的各项特性,因此能够预估最终乘波体形状且参数调节较为形象方便,但是最终生成流场参数不可控。
2) 基准流场的生成体物面压强参数可控相当于将乘波面压强作为基准流场的可调整设计参数,方便设计前体与进气道物面压强给定的乘波体构型,对乘波体的升阻力及俯仰力矩能够进行相对准确的控制。
3) 基准流场的生成体物面马赫数可控相当于将乘波面马赫数作为基准流场的可调整设计参数,一定误差范围内能够设计且方便调节进气道出口截面给定马赫数的乘波构型。
4) 基准流场的前缘激波可控相当于将前缘激波形状作为基准流场的可调整设计参数,对设计复杂波系或者强压缩的乘波体构型较为灵活。
5) 基准流场的多参数组合可控即根据气动布局的设计需求自由组合选择设计参数,最终生成满足设计目标的高超声速气动布局。
2.3 基准流场的求解方法
基准流场的求解方法多种多样,主要包括斜激波关系式方法、Taylor-Maccoll流动方程求解法[75]、高超声速一阶小扰动理论、二维特征线方法、CFD方法(包含有限差分法和有限体积法等)。
斜激波关系式方法只能应用于二维或准二维的直线激波的波后流场近似求解,如简单的楔导乘波体基准流场的求解。
TaylorMacoll流动方程只能应用于内/外锥形流场的求解,最典型的是Mölder提出的四种内/外锥形流场:三维绕圆锥外流场、Busemann内锥形流场、内锥形流场A (Internal conical flow A)、内锥形流场B (Internal conical flow A),如图21。这类流场的简化特征是,沿流场中某一点发出的所有射线上的气动参数相同,气动参数只与初值和射线偏角有关。需要注意的是Taylor-Maccoll方程在数学上存在奇点,反映在流场中会在奇点处出现非物理间断解,因此自变量的可行域会变窄,流线追踪必须在可行域范围内的基准流场中进行。
高超声速一阶小扰动理论是在三维轴对称圆锥绕流流场基础上拓展开来的,即在轴对称绕流的基础上对变化的参数近似为小扰动变量,进行一阶小扰动线化,忽略高阶偏导,最终求得小扰动后的流场参数。Rasmussen[86]将轴对称绕流横截面标准圆曲线添加椭圆偏心率的扰动变量,求得三维非轴对称椭圆锥绕流基准流场。Lin[89]在Rasmussen工作基础上,又将纵向直母线变为椭圆段型线,求得三维非轴对称横向和纵向椭圆偏心率都可控的基准流场。因此高超声速一阶小扰动理论可应用于三维非轴对称类锥类绕流流场的求解。
二维特征线方法可应用二维无旋流场和三维轴对称有旋流场的求解,特征线法对边值条件或者叫初值条件有一定的范围限制。如图34所示,第一类边值条件:已知定常超声速流场中的某一条非特征线的普通曲线AB上各点的位置坐标和流动参数,求取过AB线以及过A、B两点的特征线所围成的区域内的流动情况。第二类边值条件:在物理面上给定过某点D的两条特征曲线AD和CD以及沿线的流动参数分布,求取四边形 ABCD区域的流动情况。第三类边值条件:给定流场的一段特征线AC上的流动参数分布,另外给定一段过A点的固壁面AB几何参数或者物理参数,求曲线三角形内ABC的流动情况。

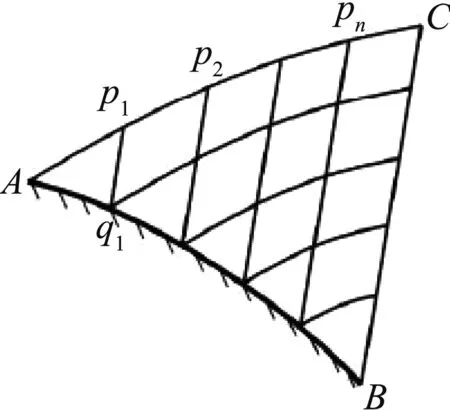
图34 二维特征线法三类边值条件Fig.34 Three types of boundary conditions of 2D MOC
CFD方法[39-40]可应用于求解各种二维或者三维流场,无论微分形式的有限差分法还是积分形式的有限体积法,都对生成体形状和流场初值条件没有特别的要求,所以在三维非轴对称基准流场的求解上相对其他方法有明显的优势。但是CFD方法因为数值耗散的缺点,计算流场中的激波有一定的厚度,很难进行精确的激波捕捉。同时由于计算耗时较多的缘故,在气动布局几何参数化优化设计上没有其他流场解算方法效率高。
通过对比上述研究概况,可以对基准流场求解方法总结为:
1) 斜激波关系式方法只能求解二维问题,应用范围较窄。
2) Taylor-Maccoll流动方程求解法只能应用于Mölder提出的4种三维轴对称内/外锥形基准流场的锥导或吻切锥乘波体设计。
3) 高超声速一阶小扰动理论是在三维轴对称锥形流的基础上对生成体曲线添加纵向或横向的小扰动,可应用于三维非轴对称基准流场的生成,该方法需要数学推导且应用范围较窄。
4) 二维特征线方法通过求解吻切面内轴对称流场可以构建较为复杂的基准流场且计算量较小,特征线法只能求解等熵及特定边界的流动,基于特征线法乘波体设计方法应用范围广。
5) CFD方法基本可以求解所有类型基准流场,但是计算量大激波捕捉精度低,不适合快速设计、优化设计及波系复杂的乘波体布局设计。
2.4 沿展向的乘波体设计方法
为了得到比锥导乘波体更均匀的进气道入口流场,以及更适用于一般性全乘波或者一体化高超声速气动布局,不断有学者在三维轴对称基准流场的基础上进行了沿展向的乘波体设计方法的拓展。现阶段沿展向的乘波体设计方法主要有吻切锥乘波体设计方法、吻切轴对称乘波体设计方法和吻切流场乘波体设计方法,这三种方法是按照研究发展的进程进行分类的,三种方法是层层递进包含的关系。
吻切锥乘波体设计方法也被部分学者称为密切锥乘波体设计方法,最早是在1990年由Sobieczky[41]提出。Sobieczky指出在不考虑横向流动的假设下,离散在当地吻切平面内的三维超声速流动可以在二阶精度范围内用轴对称流动来逼近。因此乘波体设计的进气道唇口激波曲线不仅仅局限于锥导乘波体的圆弧,可以任意指定ICC曲线的形状,只要满足ICC曲线上所有点曲率半径中心在FCC前缘曲线的另外一侧即可,如图28,通过缩放零迎角圆锥绕流流场使底部激波半径等于不同吻切面内ICC曲率半径,得到单个吻切面内基准流场,ICC曲率半径与FCC曲线交点作为前缘点进行流线追踪,最终得到所有吻切面内流线并拟合乘波压缩面。
吻切轴对称乘波体设计方法是在吻切锥乘波体设计方法的基础上拓展开的,最早是在1995年由Sobieczky[113]、王卓和钱翼稷[33,43]等提出,吴颖川[114]等学者也有大量研究。不同于之前每个吻切面内的直前缘激波锥形绕流基准流场,Sobieczky采用了外凸形曲前缘激波生成的曲面锥流场作为基准流场,每个吻切面内通过缩放前缘激波可控的曲锥流场使底部激波半径等于ICC曲率半径得到匹配的基准流场。即每个吻切面基准流场可以不限于圆锥绕流,也可以采用其他类型的轴对称流场。贺旭照[78]在Sobieczky吻切外锥乘波体设计方法的基础,采用了内锥形基础流场拓展了吻切轴对称乘波体设计方法的应用范围。
吻切流场乘波体设计方法(Osculating Flowfield Method)是在吻切锥和吻切轴对称乘波体设计方法基础上拓展开的,最早是在2005年由Rodi[115]提出。Rodi指出每个吻切面内基准流场可以不仅仅局限于同一个轴对称流场的缩放,可以对每个吻切面单独设计不同的内凹型面或者外凸型面的基准流场。通过与吻切锥乘波体的对比,结果显示在马赫10时,无黏阻力最多有13%的减小量,同时也减小了黏性阻力和配平阻力,增大了容积率,提升了乘波体后体的封闭性,增加了质心的前后限范围。尤延铖[116]在Rodi的方法上进行了拓展,吻切流场方法不仅可以应用于外锥形乘波体的设计,而且可以应用于内锥形乘波体的设计,尤延铖通吻切流场方法构建了内锥形进气道基准流场和外升力面的外锥形基准流场,生成了基准流场完全融合的内外“双乘波”高超声速气动布局概念设计,如图35所示。该方法突破了吻切锥或者吻切轴对称方法中ICC曲线曲率中心全在FCC曲线另一侧的限制,内锥形曲率中心和外锥形曲率中心分别在FCC曲线两侧。
2.5 乘波体在高超声速气动布局中的拓展应用
乘波体的来流设计条件较为单一,因此乘波体布局多应用于为高超声速飞行器巡航状态。而实际高超声速飞行器飞行包线范围较大,既要满足大空域,又要满足大速域,所以不断有学者试图拓展乘波体设计方法在高超声速布局中的应用范围,主要方法有不同构型的串并联、基准流场的串并联、全乘波布局及一体化耦合[117]等。
2.5.1 不同构型的串并联
2006年,Matthews[118]提出了一种适用于高超声速发动机进气道的多模块乘波进气道设计方法。该方法采用了等直面或等压力三维轴对称内锥形基准流场,FCC曲线为扇角为2π/N(N个模块)的扇形曲线,如图36所示,扇形圆心在基准流场物面上,扇形圆弧中点在基准流场对称轴上,因此最终生成的单个模块都包含尖锥和溢流口。图中也展示了四个模块的发动机进气道。相比于一般乘波进气道,该方法生成的布局能够显著提升进气道在不同迎角和侧滑角下进气捕获量,同时溢流口能提升发动机的启动性能。该方法是乘波构型的多个并联布局。


图35 双乘波原理示意及三维气动布局Fig.35 Dual waverider configurations


图36 进气道FCC曲线及多模块乘波进气道Fig.36 FCC and modular inward turning inlet
2009年,王发民[119]提出了如图37所示的宽马赫数范围的两级串联高超声速气动布局设计方法,该方法基于吻切锥理论在每个吻切面内采用Taylor Maccoll外锥形流场作为基准流场,对前后级乘波构型进行了设计,其中前体/进气道部分设计为来流马赫数6、高度30 km的高超声速巡航乘波构型,主翼部分设计为来流马赫数3、高度15 km的超声速巡航乘波构型,第二级乘波压缩面通过连接段放置在第一级激波干扰区外。该气动布局有效平衡了高速与低速不同巡航速度下的气动性能,并通过对前缘的钝化来减弱气动加热,对高超声速气动布局有一定的指导意义。李世斌[120]等也对这种串联气动布局进行过研究,但是李提出的气动布局后级乘波构型是在前级乘波体干扰区内,并且通过过渡方式进行融合。


图37 两级串联乘波布局Fig.37 Two-stage tandem waverider configuration
2015年,李永洲[102]提出了基于马赫数分布可控曲面外/内锥形基准流场的前体进气道一体化设计方法,生成的气动布局如图38所示。进气道型面通过基于马赫数分布可控的内锥形基准流场流线追踪得到,两侧前体型面通过基于马赫数分布可控的外锥形基准流场流线追踪得到,最终并联得到一体化气动布局方案,内锥形进气道能显著改善进气道出口流场的均匀性,外锥形前体能改善整机升阻特性。该方法是乘波构型的多个并联。

图38 双乘波的基于内/外锥前体/进气道一体化并联方案Fig.38 Dual waverider based on parallel inner and outer generating flowfield
此外,崔凯[121]等提出的双旁侧进气高超声速气动布局概念,将两个常规乘波前体/进气道外置机身两侧并通过钝形过渡得到整机气动布局。南向军[122]通过在压升可控内锥形基准流场中对类水滴形FCC曲线进行流线追踪得到带有尖前缘和溢流口的内收缩进气道,并与吻切锥乘波前体进行几何融合得到前体/进气道一体化气动布局。对于适用于两侧进气的类水滴型内收缩进气道,周正[123]进行了类水滴型FCC型线向圆形进气道出口的三维渐变设计。Takama[124]提出通过组合乘波体与常规气动翼来提高乘波体在低速下升阻比等气动特性的方法,研究了其在低速时的性能,研究表明加装机翼可以有效地提高乘波体在低速时的性能。为了充分发挥乘波体的优异性能。这类气动布局都是乘波构型或常规构型的多个几何并联。


图39 两侧进气并联布局Fig.39 Integration of parallel side inlets
2.5.2 基准流场的串并联
2014年,柳军[125]等提出了一种滑翔巡航两级锥导乘波体气动布局设计方法,如图40所示。该方法将两个不同来流马赫数的轴对称圆锥绕流作为基准流场,两个基准流场马赫锥相交线作为乘波体前缘FCC曲线,分别在两个基准流场中进行流线追踪,最终得到具有相同前缘曲线的上下两级乘波型面。在滑翔段将高马赫数大激波角的乘波型面作为外流罩,在巡航段抛掉外流罩,将低马赫数小激波角的乘波型面作为压缩面。该气动布局突破了乘波体构型只能在单一飞行条件下才能满足严格乘波的限制,拓展了飞行马赫数范围。李世斌[126]提出了一种沿展向两级锥导乘波体并联的方案,该方案中构建了来流马赫数分别为4和8的两个同轴并联轴对称圆锥绕流基准流场,两个基准流场激波角相同但是生成体锥角不同,因此相同的前缘曲线分段在不同基准流场中进行流线追踪,靠近基准轴的内段FCC曲线在马赫数8高速流场中进行流线追踪,远离基准轴的外段FCC曲线在马赫数4低速流场中进行流线追踪,最终生成型面进行拟合,气动布局如图41所示。该类气动布局在设计方法上是基准流场的多个并联。

图40 上下两级锥导乘波体原理图Fig.40 Two-stage waverider derived from crossing generating flowfields

图41 沿展向两级锥导乘波体布局Fig.41 Two-stage waverider with spanwise integration
2015年,吕侦军[127]等提出多级压缩的锥导/吻切锥乘波体设计方法,该方法进行了多级圆锥绕流基准流场的构建,如图42所示,最终流线生成具有三级压缩面的乘波布局。王旭东[128]在此基础上进行多级乘波前体与截短Busemann进气道基准流场的构建及一体化布局设计方法的拓展,如图43,气动特性相比相同设计条件下多级压缩乘波体有一定的提高。该类气动布局在设计方法上是基准流场的多个串联。
2.5.3 全乘波布局及一体化布局
1993年,O′Neill和Lewis[129]提出了一种吸气式高超声速全乘波气动布局设计方案并进行了气动参数的优化设计,如图44所示。该方案是在轴对称圆锥绕流基准流场的基础上对整机前缘曲线和唇口前缘曲线进行流场追踪得到整机乘波压缩面和进气道外型面,同时给定进气道型面和喷管型面,最终得到一体化气动布局。虽然进气道改变了流场,但量整机下部所有型面基本包含在前缘激波内,满足乘波特性。

图42 三级锥导/吻切锥基准流场Fig.42 Flowfield derived by three-stage cone/osculating cone

图43 三级乘波体与两级乘波+截短Busemann一体化布局Fig.43 Three-stage osculating waverider and two-stage waverider interation with Busemann inlet


图44 基准流场示意及一体化构型Fig.44 Integration of waverider and inlets
1995年,Lin[130]利用高超声速小扰动理论方法构建了具有纵向椭圆曲率母线的类圆锥绕流基准流场,如图45,分别对特殊的FCC前缘型线和进气道型线进行流线追踪得到乘波前体/进气道/主翼一体化压缩型面,并利用楔导乘波体设计了双垂尾。
2015年,丁峰[131]提出了一种全乘波布局的设计方法,即飞行器前体、机翼、机身全部满足乘波特性的整机气动布局,如图46。
该方法采用基于特征线法的三维轴对称类锥形绕流作为基准流场,给定轴对称旋成体母线各段型线方程,并对基准流场进行求解。该方法中的生成体为类纺锤形,先压缩后膨胀收缩;前体前缘、进气道唇口和机翼前缘贴附于基准流场激波面,通过流线追踪的气动布局继承了生成体的气动特性,前体进气道前乘波型面有效压缩来流,唇口之后机身及机翼适度膨胀有利于减小底阻。进气道内部型面通过内转向消波设计方法进行激波设计与型面捕捉。
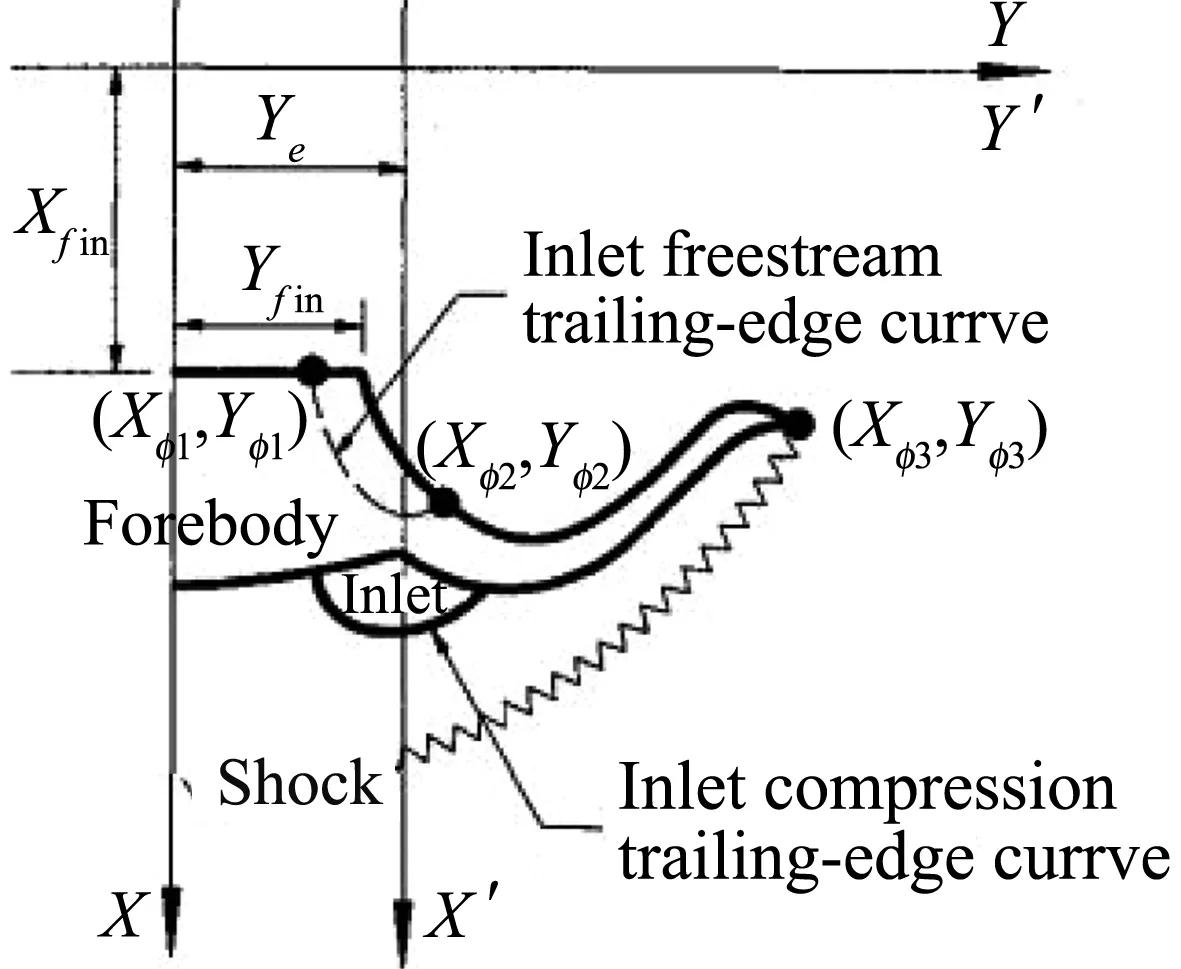

图45 前缘曲线及生成的一体化布局Fig.45 Leading edge curve integration design

图46 基准流场及全乘波布局Fig.46 Base flowfield and full wave rider design
2015年,王成鹏[132]等进行了常规乘波体与截短Busemann进气道的融合气动布局设计。内收缩进气道FCC前缘曲线为类水滴形曲线,进气道与前体共有段前缘线为外压缩基准流场激波面与内收缩Busemann基准流场前缘马赫波面相贯线,这保证了前体与进气道几何外形上的一体化融合。该方案中还对不同形状进气道FCC曲线以及进气道方转圆和扇转圆进行了一定的研究,最终并联安装了常规气动主翼,如图47所示。Smith和Bowcutt[133]在2012年也对该种布局设计方法进行过研究。Xiang[134]将截短Busemann进气道置于机身背部与常规升力体融合,并对比分析了不同进气道前缘曲线对整机布局气动特性的影响。


图47 外乘波+Busemann进气道+常规翼气动布局Fig.47 Parallel integration of outer waverider and Busemann inlet
国内外众多学者进行了将乘波体应用到高超声速飞行器设计中的工作研究,对乘波布局的一体化设计与应用有很大的推动作用。美国马里兰大学Lewis所领导的小组进行了大量的乘波体与进气道、发动机一体化方案的设计与研究[93-94,135-136]。为了充分发挥乘波体的优异性能,国外许多研究人员对乘波体构型进行了优化[67,137],Bowcutt[137]在考虑黏性之后对乘波体构型进行了黏性优化。Wilson[138]研究了前缘钝化对升阻比的影响,得出升阻力和前缘气动加热是相互矛盾的设计目标,需要进行优化以获得满足升阻力和气动热要求的最优外形。国内研究者也对乘波体进行了广泛的研究,并提出了一些比较新颖的乘波体设计方法。贺旭照[73]在研究中指出,对于以吸气式超燃冲压发动机为动力的高超声速飞行器来说,基于传统乘波体设计方法设计的乘波体对来流气体的压缩量不足,不能满足进气道内收缩段入口对气流参数的要求。为了解决传统乘波体压缩量不足的问题,贺旭照[73]发展了一种密切曲面锥(Osculating Curved Cone,OCC)乘波体设计方法,该乘波体前部分采用传统的直锥乘波体设计方法,后接曲面锥等熵压缩段,再接直线过渡段,该型乘波体克服了传统乘波体压缩量不足和容积率小的缺点。贺照旭[140]等发展了一种密切曲面内锥乘波前体进气道(Osculating Inward turning Cone Waverider Inlet,OICWI)的一体化设计方法,通过数值模拟和风洞试验验证了设计方法的正确性。王发民[96]提出了用相交楔锥流场构造乘波构型飞行器前体的方法。该方法利用无黏相交楔锥流场生成具有两个压缩面的乘波前体,使前体的预压缩能力得到充分的发挥。同时用数值模拟的方法研究了不同前体压缩角度组合的预压缩效果,并在压缩角优化的基础上进行了前体/进气道的一体化设计[95]。吕浩宇[141]研究了乘波构型飞行器前体和磁流体进气道一体化设计,得出对进气道引入磁流体流动控制技术不仅可以将高温高马赫数来流中的部分能量转化为电能, 还有利于提高燃烧室的热效能,磁流体流动控制技术可以有效地提高进气道的性能。
从上述分析可以看出,乘波体在高超声速气动布局中的拓展应用包括但不限于:不同构型的串并联、基准流场的串并联、全乘波布局设计及一体化耦合设计等几个方面,其主要特征可以归纳为:
1) 不同构型的串并联多为气动布局模块化的串并联,不同模块之间无强耦合关系。
2) 基准流场的串并联从流场结构上进行串并联,有一定的流场结构分区和共同依赖条件。
3) 一体化耦合设计一般是在强耦合的多级基准流场中对不同功能划分的压缩面进行一体化流面追踪,最终生成一体化乘波构型。
4) 全乘波布局设计即为全机前缘线(包括前体、进气道、机翼前缘)都为乘波压缩面流线追踪的前缘线且全机前缘激波贴附在前缘线上。
3 总结与展望
综上所述,世界主要工业强国都对临近空间吸气式高超声速飞行器投以相当的研究精力,公开资料显示,现阶段还没有一款能够大空域大速域空天飞行且具备高超声速巡航的吸气式运载飞行器,但是越来越多的资料显示,高超声速飞行器的技术成熟度越来越高,已经有相关型号的技术验证机完成了部分科学验证试验,比如X-51A等。通过对主要国家典型高超声速飞行器的对比分析,可以大致归纳出高超声速飞行器的发展方向主要集中在宽速域可重复高超声速运载飞行器(如SR-72等)、窄速域高超声速巡航飞行器(如HSSW、X-51A等)和再入式高超声速机动飞行器(如HTV等)等几个方面,并且高超声速飞行器的技术重点越来越集中于机体/推进系统的一体化设计,乘波布局设计方法在机体/推进系统的一体化设计中起着至关重要的作用。
在吸气式高超声速巡航飞行器气动布局设计技术领域,随着科学技术的迅速发展以及人们对先进飞行器的渴求不断提高,在以下几个方面值得深入考虑:
1) 现阶段高超声速巡航飞行器机体与推进系统的设计比较偏向模块化,即取相对稳定的流动截面做为各部件分隔面,对前体、进气道、燃烧室、尾喷管等进行单独或部分耦合设计。随着设计方法及数值模拟方法的发展,高超声速乘波前体/进气道/隔离段/燃烧室/尾喷管超燃冲压内外流一体化设计有一定的研究价值和可行性。通过给定任务参数、推力需求等,估算来流通量需求及燃料喷射量需求等,进而开展由前往后的高超声速内外流布局的一体化设计。
2) 关于乘波布局设计在高超声速飞行器气动布局上的应用,现阶段乘波体设计主要应用于前体进气道来流预压缩以及简单的全乘波布局设计。因为乘波体布局在设计来流马赫下具有相对理想的气动特性,较适合如高超巡航弹等速域较窄的飞行器,但是水平起降高超声速飞行器(如SR-72)除了巡航状态外速域范围较大,所以乘波布局的设计也要考虑跨速域气动特性。因此高超声速前体、机身、机翼全乘波布局设计有一定的研究价值,其难点在于兼顾跨速域气动布局的设计,及克服全乘波机身尾部尾部截断过大造成的底阻过大问题。
3) 现阶段单一动力形式无法满足高超声速大速域飞行的要求,因此出了涡轮基组合动力(TBCC)或者火箭基组合动力(RBCC)等一批解决方案。但是高超声速飞行器动力系统的布局是跟全机气动布局高度耦合在一起的,尤其是前体与进气道的一体化设计,几乎没有内外流的严格区别。因此在乘波前体与进气道的一体化布局设计以及喷管的设计上,必须考虑组合动力系统的模态转换问题。
4) 现阶段完全有效的转换技术还没有可靠应用案例,并且转换马赫数多高于涡轮发动机速度上限并低于冲压发动机速度下限,处于空档衔接段。因此乘波布局设计对模态转换的影响必须进行细致的研究分析。
本文对高超声速巡航飞行器乘波布局气动设计技术进行了综述,通过对比分析给出了一些结论,并对今后发展方向进行了展望。受本人知识所限,文中不妥之处敬请各位同行批评指正。
致谢:感谢国家自然科学基金、航空科学基金、南京航空航天大学创新基金及国家“863”计划等对本文研究工作的大力支持与资助。
