高维度气动优化问题的可视化方法

卢吉承, 宋文滨,*, 郑彭军

(1. 上海交通大学 航空航天学院, 上海 200240; 2. 宁波大学 海运学院, 浙江 宁波 315211)

0 引 言

高可信度的数值分析工具在飞机设计中的应用越来越普遍，基于包括计算流体力学(Computational Fluid Dynamics，CFD)和有限元模型(Finite Element Methods，FEM)等方法的高维度优化问题是工程应用中普遍存在的优化问题。高维数优化问题的可视化，属于数据可视化领域中的一种，其难点在于如何使用合理而有效的方法，通过低维度空间来可视化高维度的数据，揭示高维度数据中的信息。对于特殊的情况，需要研究者改进或发展专用的显示工具，这是一项不小的挑战。用户可以通过可视化工具，方便准确地发现高维度数据中的参数相互关系，便于设计师调整参数范围，从而帮助用户做出有效的决策。针对高维数气动优化问题，在有限的数值计算的约束条件下，找到复杂参数关系之间的最优组合。因此，将气动优化问题和高维度可视化方法有机结合，具有非常重要的应用价值。

传统的优化设计流程中，仿真分析模块就像是一个“黑匣子”，设计者输入参数，通过不同的优化算法组合，得到优化结果，并进行后处理分析。但是，对于优化流程中，参数之间的关联关系，参数与响应值之间的关系，设计者都难以得到实时和全面的信息。所以，本文根据样本数据，对设计参数之间以及其和响应函数之间的关系进行分析，揭示参数设计空间以及响应面的分布情况，更好地控制参数范围，有效减少耗时的CAE(Computer-Aided Engineering)分析计算次数，提高优化效率。

在20世纪70年代，一些欧美学者首先提出了可视化技术。Chernoff 在1973年提出了脸部图的可视化理论方法[1]。脸谱图是以人脸的特征(比如眼睛、眉毛、鼻子等)分别映射数据项的每一个属性。脸谱图可以直观地从大量数据中发现异点，且可以根据表情来对数据进行聚类。但是，该可视化方法仅适用于维数不多的数据集。到了20世纪八九十年代，出现了多种可视化技术，比如，1983年Littlefield[2]提出了符号图的概念，1984年Cleveland和McGill[3]提出了散点图矩阵的方法，1985年Inselberg[4]提出了平行坐标系的可视化方法，1996年Keim[5]提出了像素图的概念。随着可视化技术的不断发展，可视化领域逐渐衍生出许多新的可视化研究方向，包括数据可视化[6-7]，科学计算可视化[8-9]、信息可视化[10]、知识可视化[11]等，本文的研究问题属于科学计算可视化领域。

在优化问题中的可视化一般都是基于二维或三维的常规技术来实现，主要包括数据分析和数据显示两个部分。数据分析是对数据中的某些特征进行挖掘和分析，找出数据集中的信息和特征，为数据显示做好准备。数据显示是指基于数据分析后的结果，通过合理的显示工具，将数据中的信息展现给用户。目前，大部分的可视化研究集中在如何根据特定的问题，选择合适的数据分析方法和显示工具。Richardson等[12]利用二维CSOM(Contextual Self-Organizing Maps)方法来显示高维数的设计空间。Duque[13]等针对大量CFD计算，采用SPOD(Snapshot Proper Orthogonal Decomposition)方法来缩减数据维数，并利用FieldView软件来可视化数据。雷琴琴[14]则提出了一种改进后的基于像素的可视化技术。

此外，还有一些可视化软件和设备也随着可视化理论的发展而相继出现。比如，美国佐治亚理工大学研发的CoVE(Collaborative Visualization Environment)[15]，CoVE是一种先进的可视化环境，提高了飞机设计流程的速度、可信度以及透明度。另外，还有一些实用的可视化软件，如OpenDX，AVS，NAG Explorer，Khoros以及虚拟现实3D技术[16]。随着可视化理论的迅速发展，可视化的种类也越来越多，可视化软件也逐渐丰富，应用领域也越来越广泛。

在现有的典型商业优化软件(比如iSight[17]，ModelCenter[18]，Optimus[19])中，也已经实现了比较丰富的可视化功能。这些商业软件的共同特点是可以通过一种搭积木的方式快速集成各种仿真软件，将所有设计流程组织到一个统一、有机和逻辑的框架中，自动运行仿真软件，并能够实现自动重启设计流程。但对于可视化方法，三种软件有着不同的实现方式。提供的可视化方法一般可以包括二维或三维数据的图形显示，以及优化过程的监控。例如iSight在用户界面上通过图形或表格的形式实时监控设计过程，用户可以随时修改设计定义，改进设计计划，除此之外，还提供量纲分析，达到减少参数的数目的目的。ModelCenter通过地毯图观察设计空间内的约束之间的关系，并且能够通过色谱反映数据优劣，同时实现多维数据可视化(如平行坐标、柱状图等)。Optimus具备分析输入与输出参数之间的敏感度关系的功能，同时还能够以二维、三维和等高图分析响应面。商业软件之外，研究人员也研究了可视化方法和优化问题相结合的处理方法，包括利用高性能计算工具(High Performance Computing, HPC)和替代模型方法提供可视化所需的大量数据[20]，这些方法或者借助上述提到的商业软件来实现，或者开发了专用的工具。但是这些软件中的可视化方法没有超越二维的数据显示，也缺乏用户实现定制可视化功能的灵活度。

本文提出一种基于MATLAB的、开放的、模块化的复合可视化架构，以及具有一定一般性的数据可视化流程，可以灵活地实现数据分析、优化流程、代理模型，以及多种可视化方法的灵活组合。同时，首次提出了立方可视化方法(Cubic Contour Plot)，发展了复合、动态HAT(Hierarchical Axis Technique)方法，给设计者提供多种选项，用以分析高维度的数据，及时改变优化决策，提高优化效率。

1 常用可视化方法

随着当今高性能计算能力的提升，以及大数据、云计算等领域的全面发展，科学工程等领域所产生的数据越来越多，而且这些数据基本都是多维度甚至是达到上千变量的高维度、非结构化问题。需要利用有效的可视化技术来协助分析这些数据的内部关联关系及隐含的信息。

可视化技术是利用计算机图形学和图像处理技术，将数据转换成图像显示在屏幕上，并进行交互处理的理论、方法和技术，其中包括数据分析和数据显示两个主要方面。

关于可视化显示方式，按照原理的不同，主要可分为：基于几何的技术、面向像素的技术、基于图标的技术、基于层次的技术以及基于图形的技术等。科学与工程问题中采用的几种常用可视化方法包括平行坐标法、散点图矩阵、热图、等高线图等等。

平行坐标法是通过多条平行且距离相等的垂直坐标轴，对应高维数据的每一个属性。其优点在于，对低维度的数据，使用平行坐标能够清晰地反映每个数据的属性，便于用户观察和理解；其缺点在于，对数据维度不是太高时，会造成大量折线交叉，图像模糊难以观察。另外，当数据间关系复杂时，整个平行坐标会变得杂乱不堪，不能够明显反映数据间的关系。

散点图矩阵是基于散点图的思想，在飞行器设计、汽车设计等实际工程领域应用广泛，但是其缺点在于，散点图只能分析两个维度之间的关系，不能同时反映多个维度之间的关系。另外，当维数较大时，矩阵显示的范围会显示区域大小的限制。

热图是一种面向像素的可视化技术。热图能够显示大量的数据，而且同时不损失相关信息。因此，热图在科学研究和处理实际问题中有着广泛的应用，比如分析随机数据、运动员体测数据等[21]。

在飞机设计领域，通过散点图矩阵、平行坐标等可视化方法，设计者可以得知设计空间中，参数与参数、参数与目标值之间的关系。另外，还可以看出部分不合格的CFD模拟数据，从而方便设计者将其从原数据集中去除。除了传统的散点图、平行坐标法之外，自适应映射图(Self-Organizing Map， SOM)、分级坐标轴技术(Hierarchical Axis Technique， HAT)以及衍生拓扑图(Generative Topographic Mapping， GTM)等可视化方法也有具有应用价值[22]。

可视化方法的共同特点在于能够将原来复杂的多维设计空间降低为二维图来进行展示，并且可以用来展示优化收敛轨迹[22]。此外，柱状图、盒图等可视化方法也有机翼设计方面的应用[23]。对于实际的飞机设计问题，设计者可以通过各种可视化方法的组合来全方位地显示设计空间，从而有助于用户了解参数关系和变化趋势，提高设计过程的效率。

2 气动优化问题的可视化需求

对于优化问题，其特点在于多参数、多目标、多约束。典型的基于优化的设计流程主要包括三个部分：问题定义、采用分析模型计算、运行优化算法寻优。但是，由于在设计初始，设计目标和约束的定义可能存在问题，导致最终优化的结果并不满足实际需求，所以，人们需要可视化工具对整个设计空间进行探索，对优化进度进行实时的评估，而不是仅仅依靠传统的优化方法[24]。

目前的优化问题的另一个特征在于大计算量，特别是高性能计算的飞速发展，使得设计者能够运行更高精度、更大规模的计算，从而获得海量的数据。对于飞机气动设计者来说，如果能够在运行大量的CFD计算之前，通过系统的、有限的样本数据的处理，以及可视化技术初步了解整个设计空间的基本特征，比如参数与参数、参数与目标值的相互变化趋势，那么就能够节省计算资源，进而大幅度地提升整个设计流程的效率。Stump等[25]利用可视化工具ATSV(Applied Research Laboratory’s Trade Space Visualizer)，人为地在受关注区域加入样本点，减小克里金模型响应面和真实值得误差，这样既可适当避免大量无效的计算，同时又方便用户了解设计空间的变化特性，获得更精准的响应面模型。Ghosh等[26]利用可视化方法来分析飞机概念设计阶段的诸多技术不确定性因素，通过灵敏度矩阵和关联度矩阵的可视化方法，设计者可以清晰地得知飞机设计参数间的相互关系，做出相应的决策。

所以，针对气动优化问题的特点：多参数、多目标、多约束、大计算量，作者认为有必要发展一种基于现有工具的、复合的可视化方法，设计者不但可以使用现有的可视化方法，还可以不断发展新的方法，从而能够有助于设计者分析高维气动数据(样本点分布情况、参数之间的相关性、响应面分布情况等)，提升优化流程的效率。

3 面向优化问题的可视化方法及工具实现

传统的优化流程如图1所示，针对特定的优化问题定义，首先利用试验设计(Design of Experiment， DoE)方法(比如拉丁超立方法、全因子法、随机均布法等)，在设计参数空间内进行取样，获得初始样本点；其次，利用数值计算程序或者商业模拟软件，计算得到相应的目标值，并在此基础上，建立响应面；然后，采用优化算法对响应面进行寻优，找到响应面上的最优点，并依据一定策略(比如按最大/最小距离法加入新样本点、加入最优点等)，向原样本集内增加样本点；随后重复以上步骤，直到优化结果收敛，获得最优的参数组合。

因此，针对该典型优化流程，本文提出了一种具有一定一般性的可视化流程(如图1所示)，通过不同的可视化方法组合，帮助用户分析高维数据，从而改善用户的优化决策，比如扩大/缩小参数空间、局部加点、偏移参数范围等。

在优化过程中，在参数空间不变的前提下，为避免产生过多的冗余信息，并不需要将每一次优化迭代后得到的参数空间或响应函数展现出来。作者认为，对于优化问题，应该在一定的迭代次数后，即达到一定的收敛效果后，此时通过可视化方法，展示参数空间，给用户提供调整参数范围的依据，以便获得更好的优化结果。

如图2所示，选取最近两次的优化结果，如果两者之间的比值在0.9与1之间，则认为该优化已产生收敛效果，此时将当前的样本数据提取出来进行分析。当维度是三维或小于三维，可以使用少量的可视化图，就能够展示参数空间，比如运用样本散点图矩阵展示各样本点的分布情况，判断是否需要在局部空间加点；运用平行坐标图，显示整体样本点的分布情况，并显示最大与最小目标值所对应的参数组合，判断是否需要针对参数空间进行缩放以及偏移等操作，并在调整后的新参数空间内补充取样；另外，通过二维响应面以及约束边界，也可以找到满足优化约束条件的区域，从而修改原参数范围。

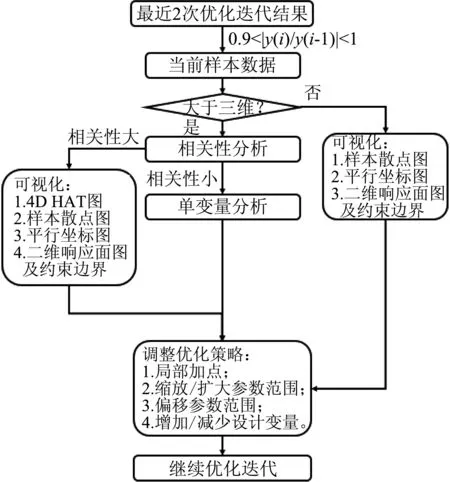
图2 可视化流程Fig.2 Flow chart of visualization

当数据维度超过三维，特别是高维度的数据，倘若需要展示参数空间的全貌，则需要产生过多的图表，这样反而会对用户带来干扰，所以，需要首先对参数进行相关性分析，并按照相关系数的大小，对参数进行排序分组，为用户提供可视分析的依据。对于相关性小的参数，可以选择对其做单变量灵敏度分析，通过直观的条形误差图，可以看出单个参数变化对目标值的影响，为用户调整该参数的变化范围提供辅助信息。对于相关性大的参数，除了之前运用样本散点图和平行坐标图，本文提出可动态调整的复合可视化方法，包括三参数立方响应面与动态分级坐标技术(HAT)[27]，这也是与现有其他商业优化软件所不同的地方。三参数立方响应面，是对响应函数空间进行切割，并利用三个切割平面表示通过最优设计点的三个参数之间的关联关系；分级坐标轴技术[27]，是一种多维可视化技术，该方法将坐标轴进行分级，并将相应的参数维度表示在上面。通常来说，分级坐标轴技术可以用于表示四维的数据，内坐标轴与外坐标轴的横纵坐标分别表示所选择的四个参数，最后，通过多种可视化方法的搭配，用户调整原参数范围，继续优化迭代，观察是否能够得到更好的优化结果。

本文发展的可视化工具有三个模块组成：数据存储、数据分析和响应面方法以及可视化方法(如图3所示)。数据存储格式为ASCII格式或XML格式，数据分析方法采用MATLAB分析函数corrcoef函数，分别得到皮尔森相关性系数以及p值(p值用于检验无相关性假设)，且p值越小，参数间的相关性越大。响应面方法，包括克里金法、多项式法以及径向基函数法。可视化方法主要有散点图矩阵、平行坐标图、二维响应面图、四维HAT图以及条形误差图。

该可视化工具的主界面，如图4所示，主要分为导入数据、数据分析、样本点分布图、平行坐标图、响应面图、HAT图、单变量分析以及导出数据等8个板块。各模块的功能如表1所示。

图3 可视化工具模块Fig.3 Modules of visualization tool

图4 可视化工具主界面Fig.4 Main interface of visualization tool

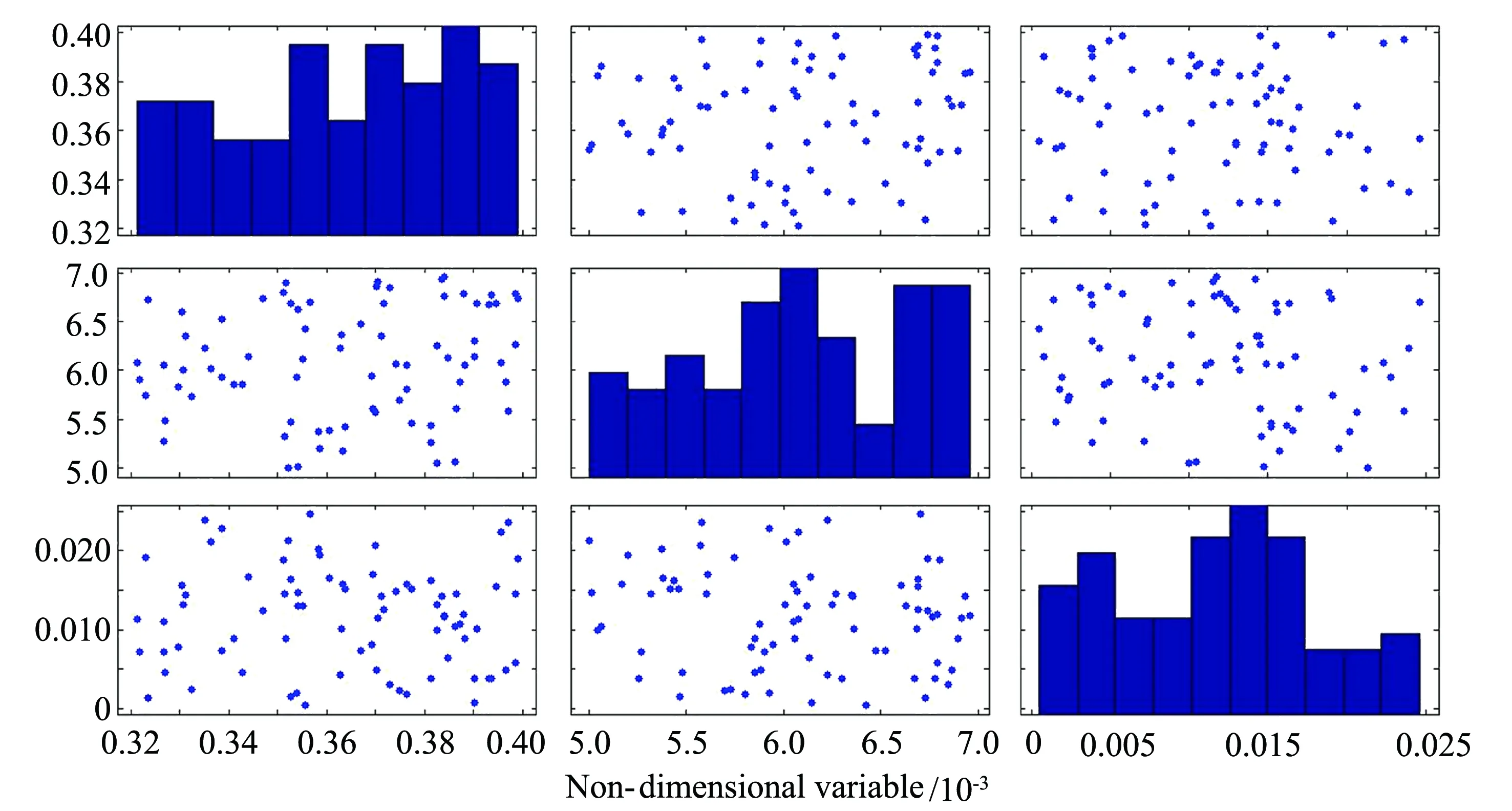
图5 样本点分布图示例Fig.5 Example of sample distribution plot

图6 平行坐标图示例Fig.6 Example of parallel coordinate plot

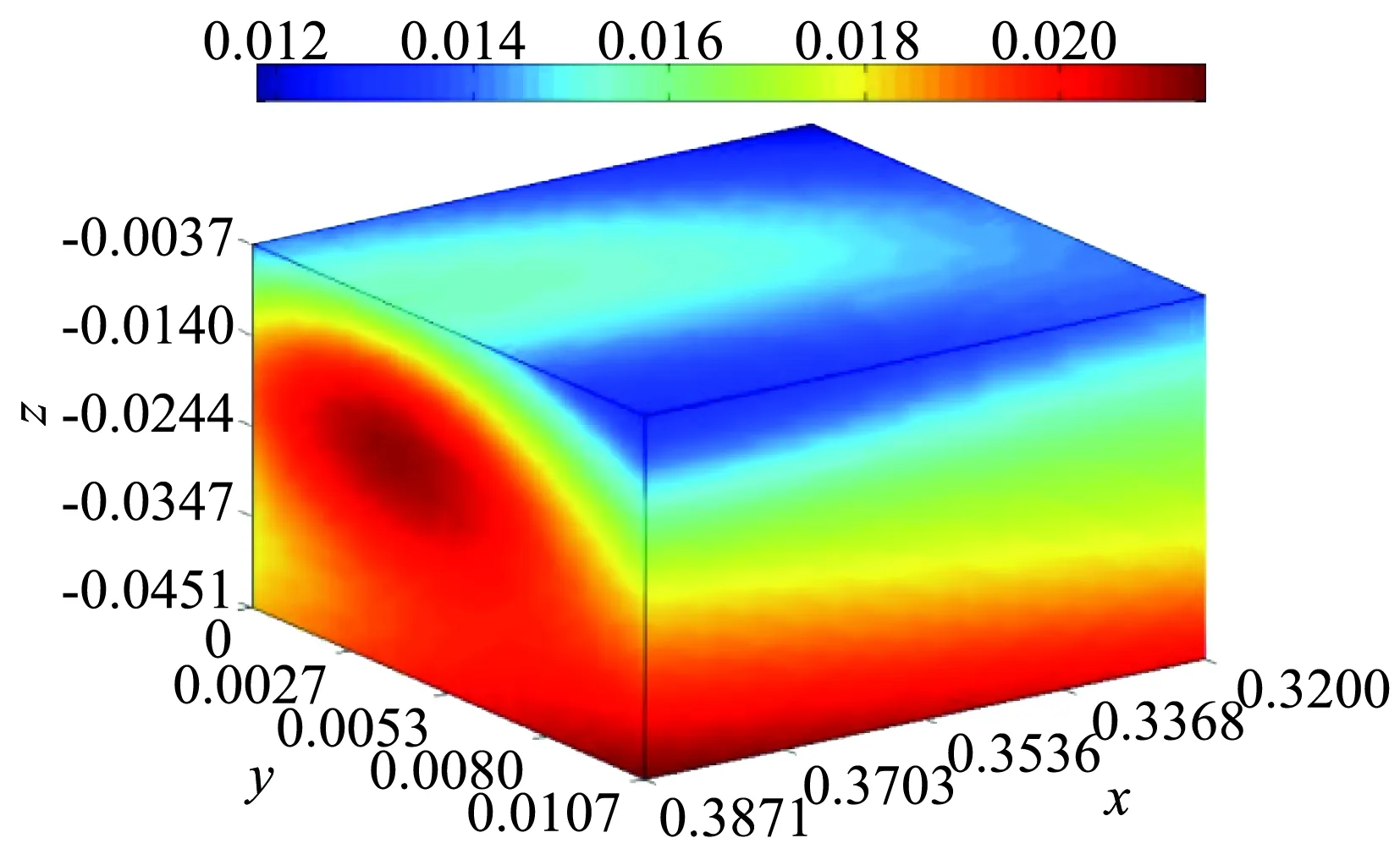
图7 三参数响应面图示例Fig.7 Example of 3-parameter response surface

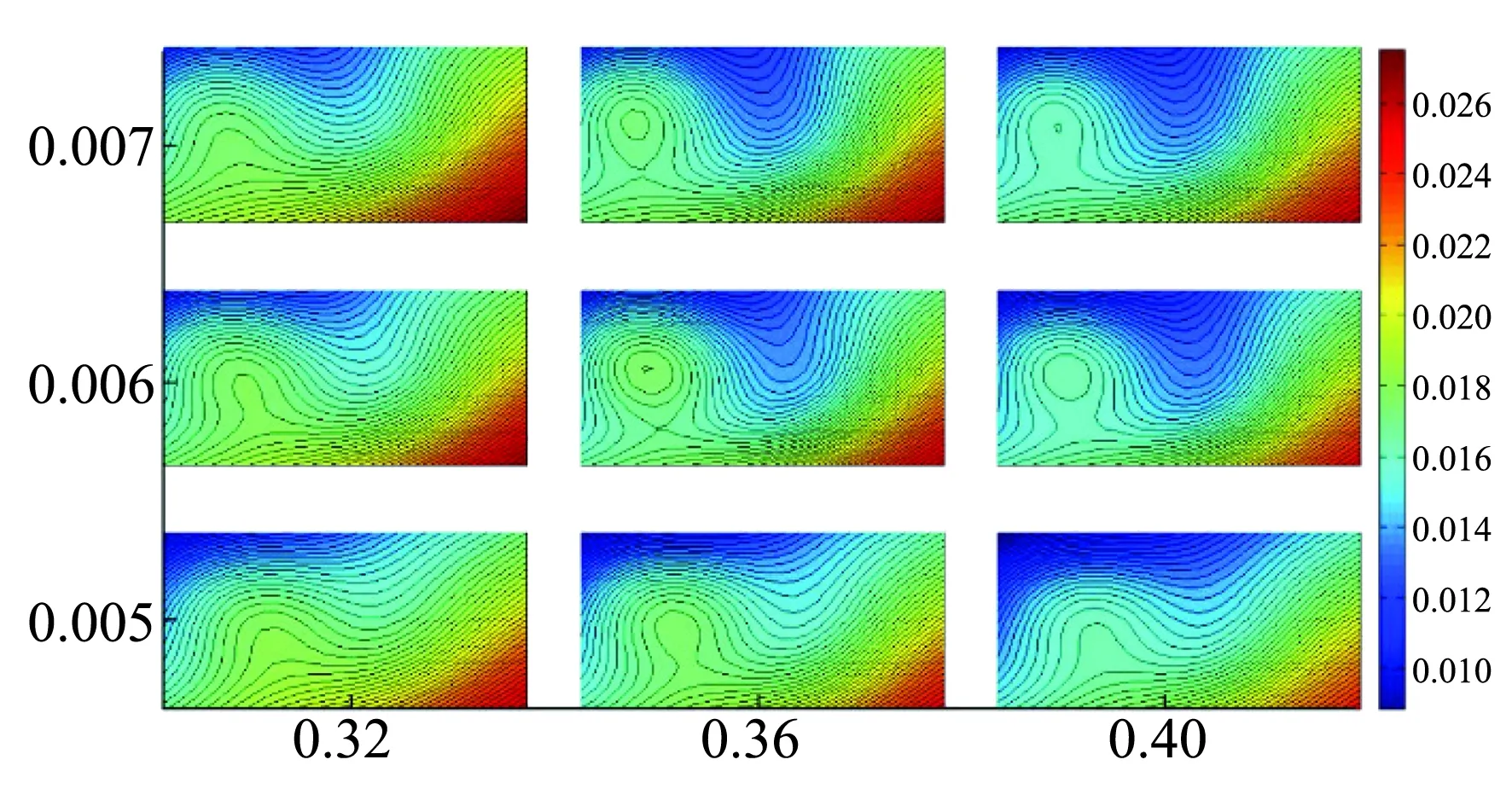
图8 四维HAT图示例Fig.8 Example of four-dimansional HAT plot

4 可视化工具的应用

4.1 测试函数——Sphere函数

此处选取二维Sphere函数，作为优化目标函数，找出目标值最小的点。二维Sphere函数的定义为：

参数范围设为x1∈[-10,-2],x2∈[2,10]，约束条件设为|x1+x2|≤5。Sphere函数的真实模型如图9(a)所示，其最优状态和最优值为f(0,0)=0。

对于该低维优化问题，通过常规的可视化方法，就可以观察到参数、响应函数以及约束条件的之间的相互关系。图9(b)显示的是参数x1与x2的初始响应面图，图中白色点区域表示符合约束条件的区域。根据图反映的信息，为了找到最优点，需要偏移原参数范围：x1∈[-6,2],x2∈[-2,6](参数空间的偏移原理为：保持原参数范围长度不变，沿着目标值变化最大梯度方向移动半个参数空间)，然后在新增加的参数范围内添加样本点继续优化迭代5步。图9(c)表示的是偏移原参数范围后的响应面图，从图中可以清晰地观察到该函数的最优点位置可能在(0，0)附近，因此，根据响应量分布范围和分布特点再次调整参数范围(缩小至x1,x2∈[-1,1])，在调整后的范围内取样，继续优化迭代5步并显示缩小参数范围后，该函数的响应面图(如图9(d)所示)。最终找到最优点位置和最优值：f(0.0027,-0.0052)=3.43×10-5，总的目标函数的计算次数为2400。

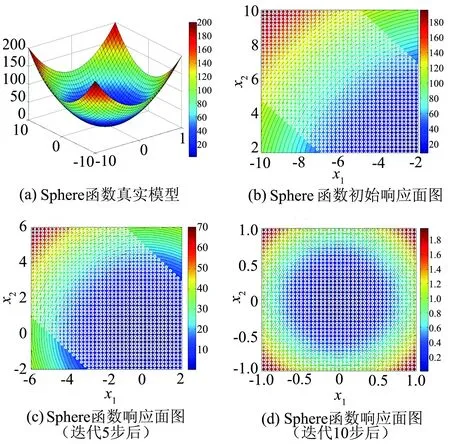
图9 Sphere函数Fig.9 Sphere function

4.2 测试函数——Rastrigin函数

此处选取100维Rastrigin函数，作为优化目标函数，找出目标值最小的点。100维Rastrigin函数的定义为：

参数范围定为|xi|≤5.12,i=1～100。Rastrigin函数的真实模型如图10所示(此处显示三维模型)，其最优状态和最优值为f(0,0,…,0)=0。

对于该Rastrigin函数，各参数是独立选取的，所以此处选取其中任意4个参数，展示其参数与响应函数之间的关系(如图11所示)。从该四维HAT图中，可以清晰地观察到参数与目标值之间的变化关系：参数在0附近的区域内，函数目标值存在最小值。因此，可以适当地缩小原参数范围：|xi|≤2.56,i=1～100(参数范围中心保持不变，将原范围长度缩减一半)，然后在新参数范围内添加样本点继续优化迭代10步。图12表示的是原参数范围缩减后的响应面图，从图中可以清晰地观察到当参数在0附近时，该函数存在最小值，因此，再次调整参数范围(缩小至|xi|≤1,i=1～100)，在调整后的范围内取样，继续优化迭代10步，并显示再次缩小参数范围后，该函数的响应面图(如图13所示)。最终找到的最优点目标值为6.667×10-4，总的目标函数的计算次数为3200。

图10 Rastrigin函数真实模型Fig.10 Real model of Rastrigin function

图11 Rastrigin函数初始响应面图Fig.11 Initial HAT plot of Rastrigin function

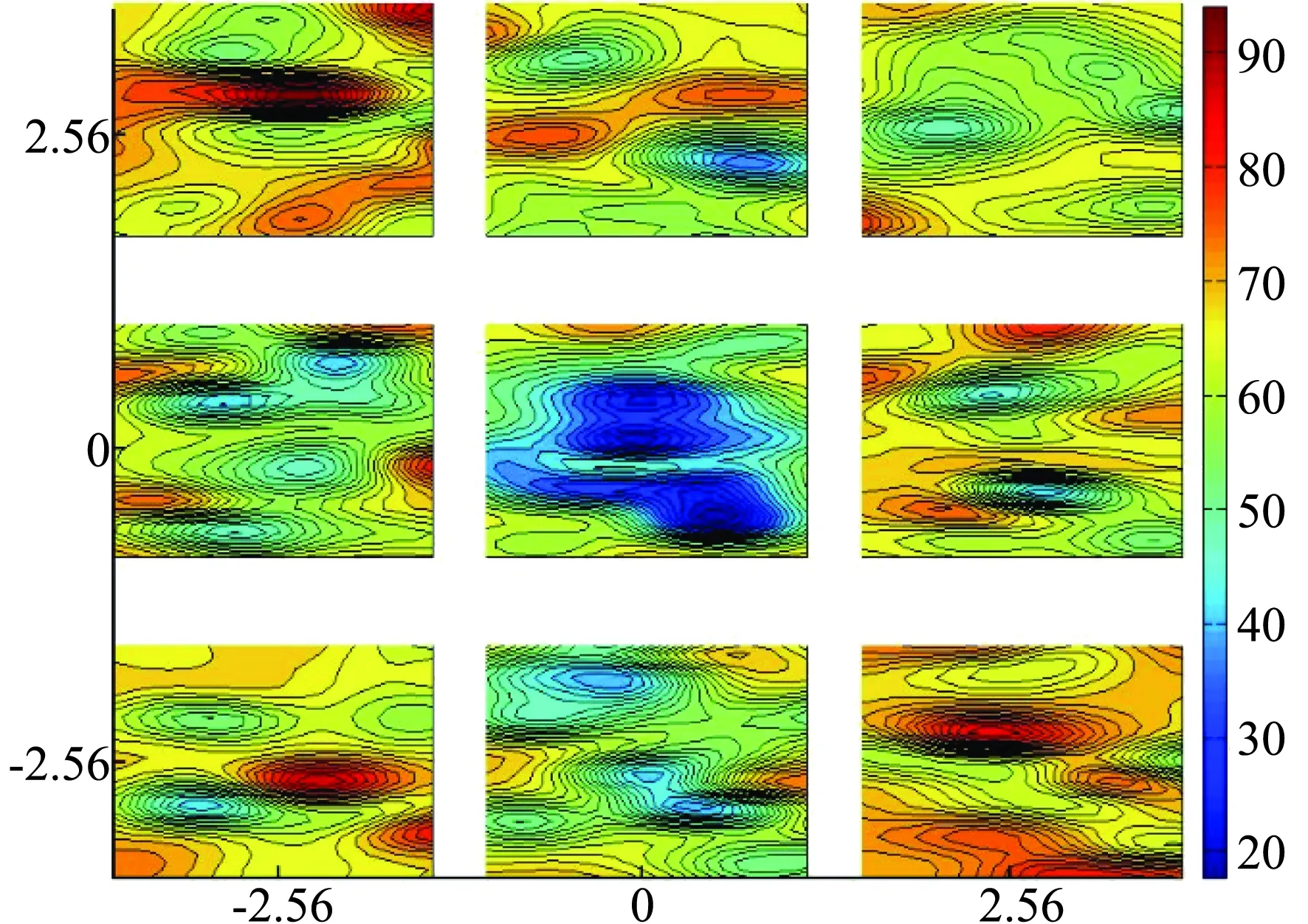
图12 Rastrigin函数响应面图(迭代10步后)Fig.12 HAT plot of Rastrigin function (after 10 iterations)

图13 Rastrigin函数初始响应面图(迭代20步后)Fig.13 HAT plot of Rastrigin function (after 20 iterations)

4.3 翼型气动优化问题

本文采用的翼型气动优化问题是针对典型的运输类飞机，在确定的升力系数CL下，优化阻力系数CD，使其达到最小值，同时满足俯仰力矩系数Cm，翼型最大厚度等约束条件。具体优化问题定义为：

(1) 设计升力系数：CL= 0.74;

(2) 翼型最大厚度：(t/c)max=0.14;

(3) 俯仰力矩系数：|Cm1/4|≤ 0.162。

飞行条件选取：马赫数为0.7115，飞行高度为36 000 ft，雷诺数为2.24×107(其中特征长度为4.35 m)。

本文采用的翼型参数化方法，是通过贝塞尔曲线，分别构造翼型的厚度曲线和弯度曲线，再将二者叠加后得到翼型外形[28]。图14和图15分别表示厚度与弯度曲线的各控制点位置关系。

图14 翼型的厚度曲线Fig.14 Airfoil thickness curve

图15 翼型的弯度曲线Fig.15 Airfoil camber curve

根据该翼型参数化方法的定义，可以将参数分为两类：特征参数和形状参数。参数的具体分类情况如表2所示，其中yB、xB为翼型最大厚度及其位置，yb、xb为翼型最大弯度及其位置，dZTE与ZTE分别表示翼型尾缘处的厚度和弯度，rLE为前缘半径。形状参数用于控制翼型的局部外形，均为无量纲化的参数，变化范围为0～1。各控制点的位置定义如表3所示。

利用该翼型参数化方法，本文分别对8个典型的超临界翼型进行拟合建模： NASA SC(2)-0714, NASA SC(2)-0610, NASA SC(2)-1010, RAE2822, Whitcomb, Boeing Airfoil J, NYU/GRUMMAN K-1 以及 GRUMMAN K-2。这8个翼型的选取原则为厚度曲线前半部分均为上凸曲线，后半部分为先凸后凹曲线，而弯度曲线前半部分均为先凹后凸曲线，后半部分均为下凸曲线。在此基础上，分析总结，得到翼型的参数设计范围(如图16所示)，使得在该参数范围内生成的翼型具有典型的超临界翼型的外形特征。

表2 翼型的特征参数和形状参数Table 2 Feature and shape parameters of airfoil

表3 翼型控制点的位置定义Table 3 Airfoil control points definition

根据翼型的气动优化流程，首先在翼型参数设计空间内随机取样，得到100个初始样本点，并将初始样本集中目标值最小的翼型作为参考翼型，然后向样本空间中增加新样本点(200个)，计算新样本点与原样本点之间的最大/最小距离，挑选其中30个新样本点加入到原样本集中，并对新样本集利用优化算法进行寻优，完成第一轮优化迭代。在此基础上，针对现有的样本集，应用可视化工具展现参数空间和响应函数。具体步骤为：

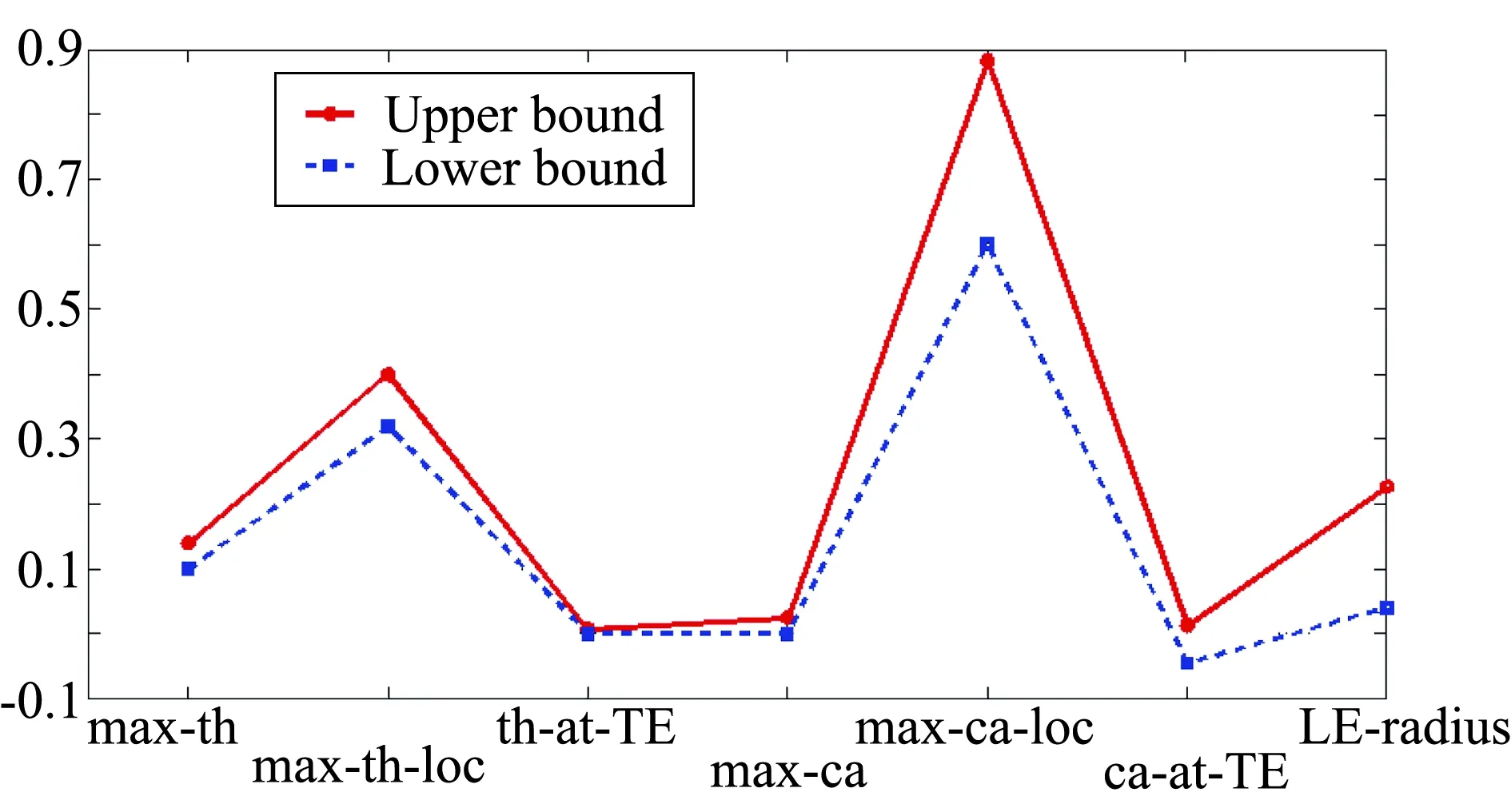
(a) 特征参数范围

(b) 形状参数范围

(1) 对当前样本集进行参数相关性分析，并按照相关性系数大小进行排序，并找出翼型特征参数的组合(此算例中为6个)，从原样本集中提取出来，形成新数据集；

(2) 对于新数据集，绘制平行坐标图，显示符合约束条件的参数组合，并显示最大与最小目标值对应的参数组合，如图17所示；

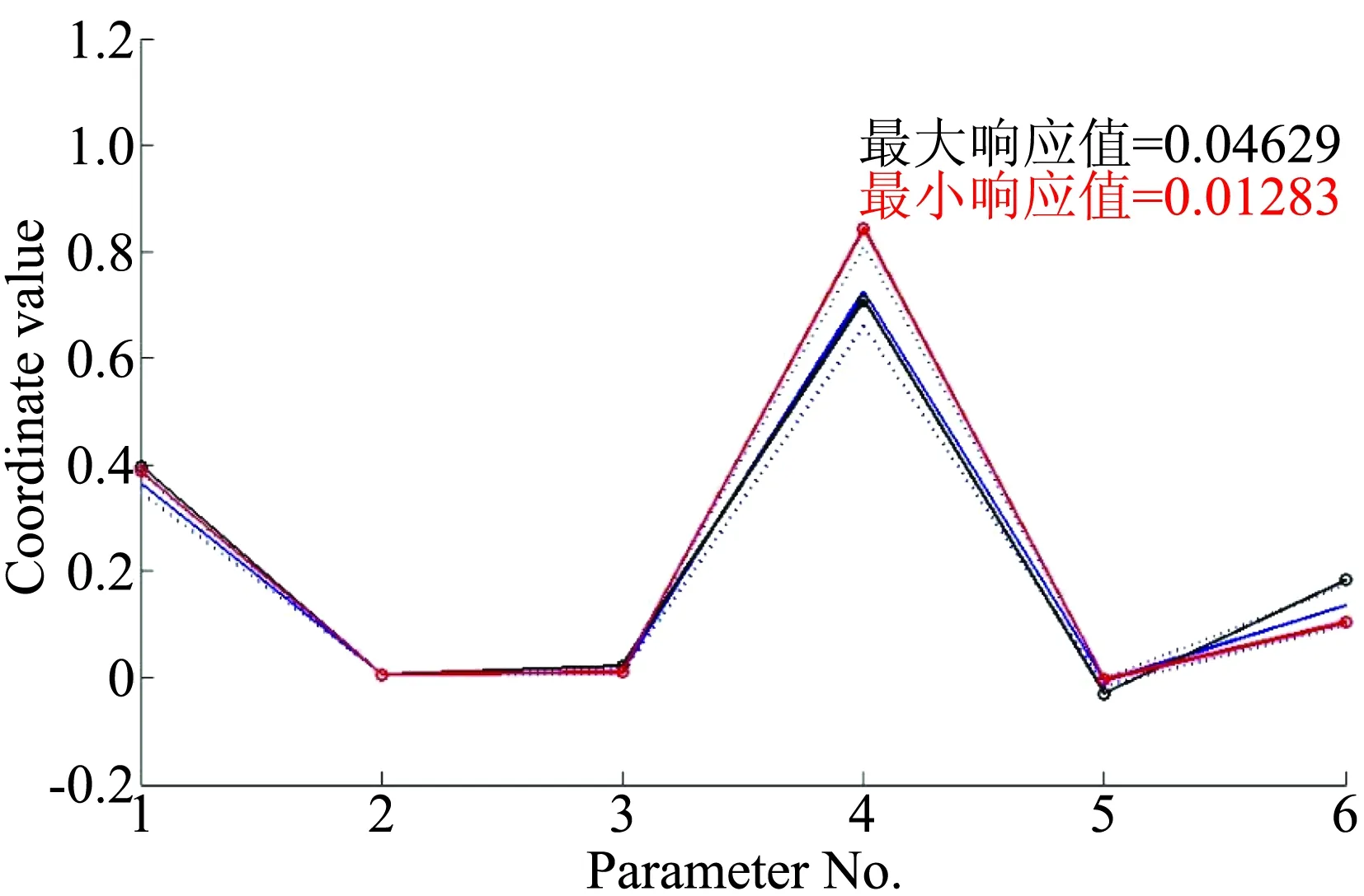
图17 翼型参数平行坐标图Fig.17 Parallel coordinate plot of airfoil parameters

(3) 对于参数相关性分析结果，绘制四维HAT响应面图，如图18所示，首先将相关性较大的参数组合置于HAT图内坐标，再将相关性较小的参数组合置于HAT图外坐标，依次类推，按照相关性排序逐级替换内外坐标的参数组合，并观察不同参数与目标值的变化关系。从图18可以看出，当翼型最大厚度位置越大，尾缘弯度越小，前缘半径越大时，翼型的阻力目标值会变小；

(a) 四维HAT图(内坐标参数：尾缘厚度x2，最大弯度x3;外坐标参数：最大厚度位置x1，最大弯度位置x4)

(b) 四维HAT图(内坐标参数：最大厚度位置x1，最大弯度位置x4;外坐标参数：尾缘弯度x5，前缘半径x6)

图18四维响应面图
Fig.18Four-dimensionalHATplotofresponsesurface

(4) 根据平行坐标图以及四维HAT响应面图，调整参数范围(首先根据响应面图中最小目标值所对应的区域，移动原参数范围的中心点，并将新参数范围长度缩减至原来的一半；然后对照平行坐标图，局部扩大或缩小新参数范围，使得当前最优翼型参数包含在新的参数范围内)；

(5) 选取相关性较小(p>0.85)的参数，对其进行单变量分析，如图19所示，水平线代表当前的目标值，竖直线代表单个变量在当前参数范围内，对目标值的影响(根据条形误差图反映的信息，以当前该参数值为中心，将参数范围缩小为原来的一半)；

(6) 在更新后的参数范围内继续取样，进行优化迭代，直至优化收敛，总的CFD计算次数为280；

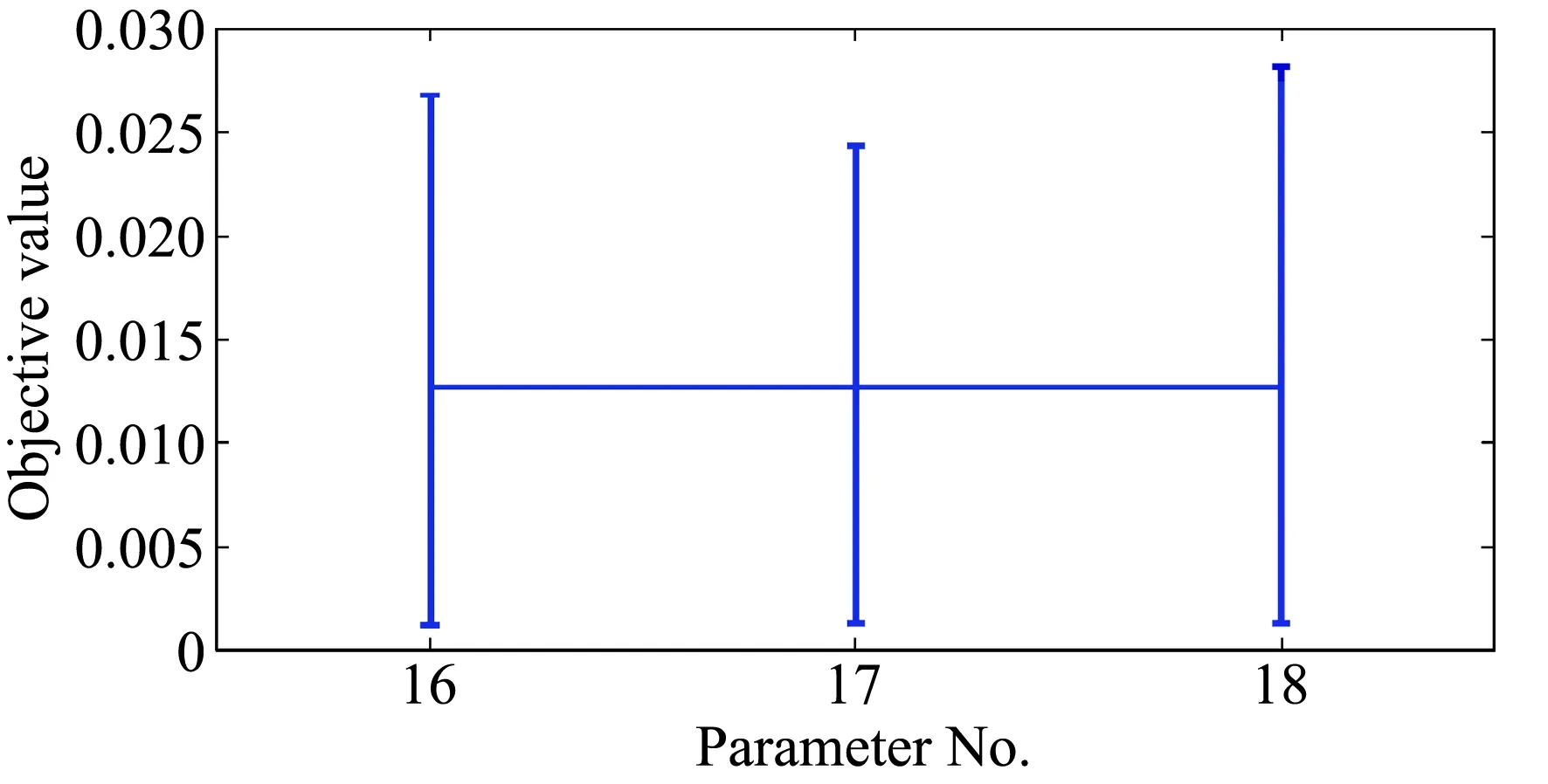
图19 单变量分析图Fig.19 Single parameter analysis plot

(7) 得到最后的优化结果。

翼型优化结果，如表4所示，可以看出对于该翼型优化问题，相比于参考翼型，最优翼型的阻力系数下降了2.5个阻力点。翼型优化收敛曲线，如图20所示。参考翼型和最优翼型的外形对比以及压力分布对比，如图21和图22所示。从翼型外形对比上，可以看出相比于参考翼型，最优翼型的前缘半径变小，最大厚度位置略微有所增大，尾缘弯度值变小。翼型的外形差异也反映在压力分布上，由于最优翼型的前缘半径更小，所以相比于参考翼型，最优翼型在前缘部分的压力差更小，逆压梯度也更小，造成翼型的阻力下降。

表4 翼型优化结果Table 4 Airfoil optimization results

图20 翼型优化收敛轨迹Fig.20 Convergence history of airfoil optimization

图21 参考翼型和最优翼型的外形对比Fig. 21 Comparison of shapes between reference airfoil and optimal airfoil

图22 参考翼型和最优翼型的压力分布对比Fig.22 Comparison of pressure distribution between reference airfoil and optimal airfoil

因此，针对典型的翼型气动优化问题，应用该可视化工具，能够反映参数与参数之间，参数与响应函数之间的关联关系，为用户调整设计参数范围提供依据，有助于设计者分析高维度气动数据。

5 结 论

本文发展了一种应用于高维度气动优化问题的综合可视化方法，该方法克服了传统优化过程的“黑箱运行”的不足，可以系统、灵活地展示高维参数空间、多维响应函数空间，以及两者之间的关联关系。利用MATLAB提供的基础数据分析功能，结合样本数据和响应面模型，用户不仅可以使用现有的可视化方法，还可以自己组成新的方法，有助于分析高维度数据。应用该可视化工具，将参数进行分组分析，通过平行坐标图、二维响应面图以及四维HAT图，综合展示了高维度参数空间、高维响应函数，不仅可以得到最终的优化结果，并且能够反映参数与参数、参数与响应值之间的变化关系，有利于用户在优化过程中，调整设计参数范围，控制所需的计算量，提高整体优化过程的效率，同时通过对优化过程的掌控，对设计变量和目标函数以及约束之间的关系得到更清晰的认知。

致谢:感谢上海交通大学航空航天学院祁洋老师对本文工作提供的帮助。