基于偏最小二乘方法的ARIMA模型在股票指数预测中的应用
2018-11-02方坷昊
方坷昊,赵 凌
(1.四川文理学院教务处,四川达州635000;2.四川师范大学数学与软件科学学院,四川成都610068)
1 引言
股票市场作为国家经济的重要组成部分,对国家经济有较强的影响,其活跃程度更是衡量国家经济的一项重要指标.此外,股票指数的上涨(下跌)幅度大小亦对投资者的投资决策有着积极(消极)的作用,间接地反馈了股市的活跃程度信息.而股票指数作为股票市场的重要综合指标,所以较普通股票而言,对股市有着更为重大的影响,更具备研究意义.
1999年,国内学者最早在国内给出了ARIMA模型在股票价格预测方面的应用;[1]2006年,覃思乾利用ARIMA模型与GM模型的组合模型对股票指数进行预测;[2]2011年,李美利用ARIMA模型对股价进行预测,并利用傅立叶修正方法进行修正;[3]2012年,王丹枫实证分析了从投资者视角来进行股票价格预测的可能性.ARIMA模型结合股票指数序列的自身规律对股票指数进行了较好的预测,但并未考虑其他的相关变量对股票指数的影响.[4]1983年,偏最小二乘回归由S.Wold和C.Alban首次提出后,该方法在关于存在多重共线性问题的解决方面迅速得到应用,在股市方面的研究亦有广泛应用,2004年,郑承利应用偏最小二乘法对美式期权的仿真定价问题进行了研究;[5]2010年,姬强应用偏最小二乘法对中美股票市场的协动性作出分析.[6]偏最小二乘回归在股票指数预测的应用上考虑了把股票指数影响较大的变量纳入自变量组进行回归分析,较好地对各个相关指标的多重共线性进行消除,但并未利用自身存在的规律性进行分析.
本文的意义在于以上证指数为例利用偏最小二乘方法对股票指数进行回归分析,将ARIMA模型得出的股票指数预测值归为原始变量组,在建立偏最小二乘回归模型时充分地利用了股票指数自身存在的规律性,且纳入投资者视角所关注的股票指数相关变量,建立了在真正意义上充分考虑了投资者行为的偏最小二乘回归模型,在统计于行为金融方面的探究中有重大意义.
2 数据与模型
2.1 数据来源
本文数据包括上海证券交易所公布的2016年1月到2016年6月上证指数数据、上证指数证券成交量、人民币对美元汇率、上证指数期货价格;美国NASDAQ证券交易所公布的NASDAQ指数数据,变量选取如下:因变量Y为上证指数当日价格、自变量X1为上证指数当日ARIMA模型预测价格、X2为上证指数上一日交易量,其数值大小代表每日交易所成交数量,一定程度上能反映短期内股民投资意愿、X3为上证指数上一日期货价格,此变量的意义在于反映市场对目标股票的涨跌期望,同时对目标股票价格具有一定的指导意义、X4为美元对人民币汇率,反映短期内金融市场的活跃程度、X5为美国NASDAQ指数价格,作为NASDAQ世界最大的股票交易市场,其指数价格作为同类型股票对上证指数价格亦具有相当的指导意义,如表1所示:

表1 变量关系表
2.2 模型理论
2.2.1 ARIMA模型
自回归滑动平均模型(Auto-RegressionIntegrated Moving Average Model,ARIMA)是由自回归模型(Auto-Regression Model,AR)、差分项I(d)和滑动平均模型(Moving Average Model,MA)两部分组成,主要用于短期时间序列建模,与传统相比,优势在于建模简便,对非线性模型有较好的解释能力.且定义如下:
若{εt}是高斯白噪声WN(0,σ2),φ1,φ2,…,φp(φp≠0),ϑ1,ϑ2,…,ϑq(ϑq≠0),皆为实数,则称
φ(B)dXt=θ(B)εt
为求和自回归滑动平均模型,并记为ARIMA(p,d,q)模型.其中B为延迟算子,d=(1-B)d为差分算子,φ(B)=1-φ1B-φ2B2-…-φpBp为自回归系数多项式,θ(B)=1-ϑ1B-ϑ2B2-…-ϑpBq为滑动平均系数多项式.
1.2.2 偏最小二乘回归模型
偏最小二乘回归(Partial Least Squares Regression,PLSR)是在1983年由S.Wold和C.Alban首次提出的, 是近年来应实际需要而生产和发展的一个有广泛适用性的多元统计方法.在常见的多因变量对多自变量的回归建模中,特别是在观测值数量少以及存在多重相关性等问题时,该方法具有传统的回归方法所不具备的意义明确、计算简便、省时、建模效果好、解释性强等优点.
偏最小二乘回归是一类解决由p个自变量X=(X1,X2,…,Xp)和q个因变量Y=(Y1,Y2,…,Yq)的n个观测值组成的数据表存在多重相关性时的回归分析问题的模型,首先偏最小二乘回归不直接对X与Y进行回归,而是先从X和Y中提取成分t1和u1,在提取成分时,有下列两个要求:
a.t1和u1应尽可能大地携带他们各自数据表X和Y中的变异信息;
b.t1与u1的相关程度最大.
在第一轮提取后,分别实施X对t1的回归及Y对t1的回归,如果回归方程已经达到满意的精度,则算法终止;否则,将利用X被解释后残余信息以及Y被t1解释后的残余信息进行第二轮的成分提取,直到达到回归方程满意精度,算法终止.
若最终提取成分数量为m,则偏最小二乘回归将通过施行yk对t1,…,tm的回归,然后表达为yk关于原自变量x1,…,xp的回归方程,k=1,2,…,q.
3 实证结果与分析
3.1 实证步骤
本文首先对上证股票指数序列进行ARIMA模型建立与分析:对股票指数序列做二阶差分处理后序列平稳,采用ARIMA模型对其价格进行一个初步的预测后,模型拟合效果较为理想,为进一步提高预测精度,根据偏最小二乘回归在处理多重共线性方面问题的优势;第二步把ARIMA模型的预测结果纳入原始变量组,记为X1、再选取上证指数上一日交易量X2、上证指数上一日期货价格X3、上一日美元对人民币汇率X4、美国NASDAQ指数价格X5四个对股票指数价格Y影响较大的变量作为原始变量组对股票指数作回归分析,利用回归分析进行拟合预测,研究表明,组合模型较ARIMA模型取得较大的修正效果.
3.2 ARIMA模型预测效果检验
3.2.1 平稳性检验

图1 上证指数价格时间序列
首先在EVIEWS软件中作出上证指数股票价格的时间序列图(图1),由时序图法,可见图像变化并不规则,不存在对于一个确定的价格附近震荡的现象,并无规律可言,认为该序列并不具有平稳性,需要对其做出差分处理;在对上证指数股票价格序列二阶差分(DDLAVE)后,差分序列在0附近震荡,初步确定平稳,对其做单位根检验(图2),可见该序列的ADF统计量的p值趋近于0,远小于0.01,通过平稳性检验,上证指数股票价格二阶差分序列为平稳序列,下面对该序列进行模型建立.

图2 单位根检验图
3.2.2 模型选择
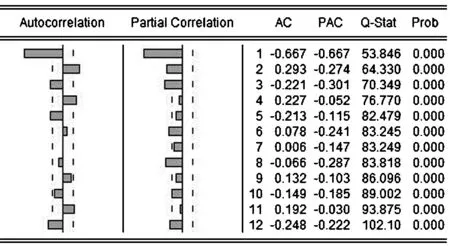
图3 自相关检验图
由自相关检验图(图3),Q统计量对应p值均趋于零,可见模型并非白噪声.我们对所要建立的ARIMA模型阶数进行确定:首先,对上证股票指数二阶差分序列做自相关检验后,得出该差分序列的自相关图(图3),可见该序列的自相关系数与偏相关系数都具有拖尾性,考虑建立ARIMA模型,有图三可见,自相关系数三阶后有迅速下降且趋于0的趋势,偏相关系数在二阶后有迅速下降且趋于0的趋势,因此建立ARIMA(1,2,1)、ARIMA(1,2,2)、ARIMA(2,2,2)、ARIMA(2,2,3)模型进行比较,模型对应结果如表2所示:
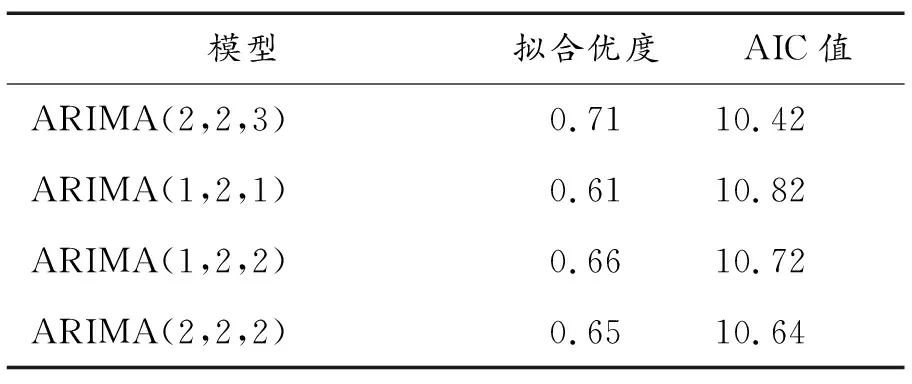
表2 ARIMA模型阶数选择
由表2可见ARIMA(2,2,3)模型在四个模型中拟合优度最大,AIC值最小,模型效果最好,所以对序列建立ARIMA(2,2,3)模型.
3.2.3 模型评价

图4 ARIMA模型
Xt=-0.905Xt-4-0.047Xt-3+1.809Xt-1-0.143Xt-1+εt+0.942εt-1-0.943εt-2-0.965εt-3
由图四可见,对该模型做t检验后,各参数对应t统计量均处在较好水平,模型系数对应p值均小于0.01,通过显著性检验;对残差做白噪声检验后,Q统计量对应p值均大于0.05,结果表明残差为白噪声,ARIMA模型为有效模型.结合上证指数与其ARIMA模型预测价格的时间序列图(图5)以及ARIMA模型对上证指数Xt的四期预测结果(表3)可见:模型的平均相对误差率为0.5%,说明ARIMA模型能较好地预测出上证指数股票价格.
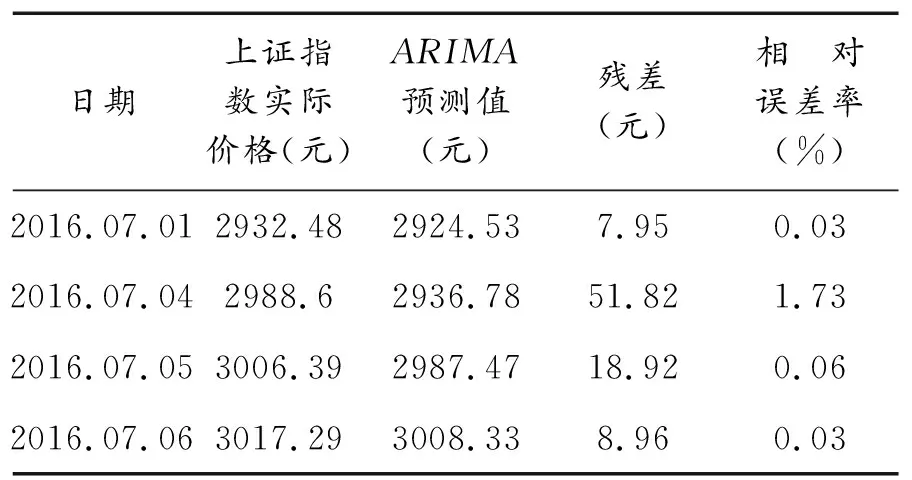
表3 ARIMA模型预测结果

图5 ARIMA模型拟合效果图
3.3 偏最小二乘模型
3.3.1 模型建立
在2.2中,通过ARIMA模型对上证指数进行拟合预测,拟合优度达到0.71,平均相对误差率为0.5%.为进一步提高预测精度,使用线性回归对ARIMA模型进行修正,基于偏最小二乘方法处理复共线性数据上的适用性:首先把ARIMA模型预测值纳入原始变量组,记为X1、再加入与上证指数价格相关的上证指数上一日交易量X2、上证指数上一日期货价格X3、上一日美元对人民币汇率X4、美国NASDAQ指数价格X5作为原始变量组进行偏最小二乘回归分析,组合模型得出结果后与ARIMA模型输出结果X1进行比较.
本文用SIMCA-P软件对上证指数Y进行偏最小二乘回归分析,输入标准化数据进行成分提取,建立解释变差表(表4)进行分析后,对模型成分个数进行选择,可以得出模型成分数量为3时自变量可被解释变差累计为96.9%,因变量可被解释变差累计为81.7%,均处在较好水平,所以确定模型提取成分个数为3,建立模型如下:
Y=30.300+0.655X1+0.010X2+0.320X3+0.027X4-0.055X5+ε

表4 解释变差表
3.3.2 模型评价
得出模型结果为数据标准化后的模型,组合模型结果较单ARIMA模型得到较大修正,拟合优度由原本的0.71上升到0.82.
通过基于偏最小二乘方法的ARIMA组合模型对上证指数Y的后四期预测值与单ARIMA模型预测值对比(表5)可见,四个上证指数预测值残差均有较大程度的减少,平均相对误差值减少27.5%.这说明基于偏最小二乘方法的ARIMA组合模型预测值较单ARIMA模型预测值效果更好,使用偏最小二乘方法的组合修正模型能够有效提高预测精度.
对模型中每个变量的重要程度作出分析:由于本文建立的模型为标准化模型,其系数只与影响方向有关,不能决定其影响大小;本文选取SIMCA-P软件中的VIP统计量(图6)对模型的每个变量重要程度作出分析,VIP统计量的值越大说明该变量的重要程度越高.由图可见,自变量重要程度排名依次为X1、X3、X5、X4、X2;说明ARIMA(2,2,3)模型的预测结果对偏最小二乘回归模型的结果影响最大.ARIMA模型在股票价格预测中通过添加相关变量做偏最小二乘回归的方法可以有效提高预测精度.
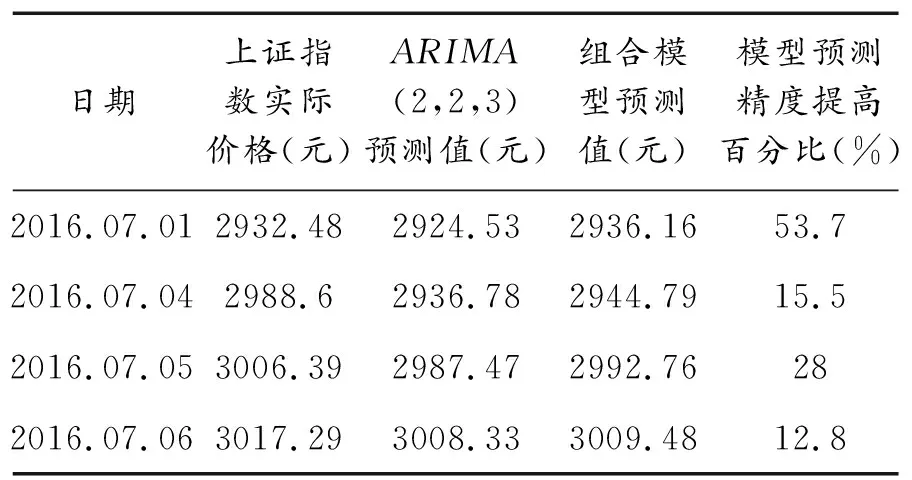
表5 组合模型预测结果
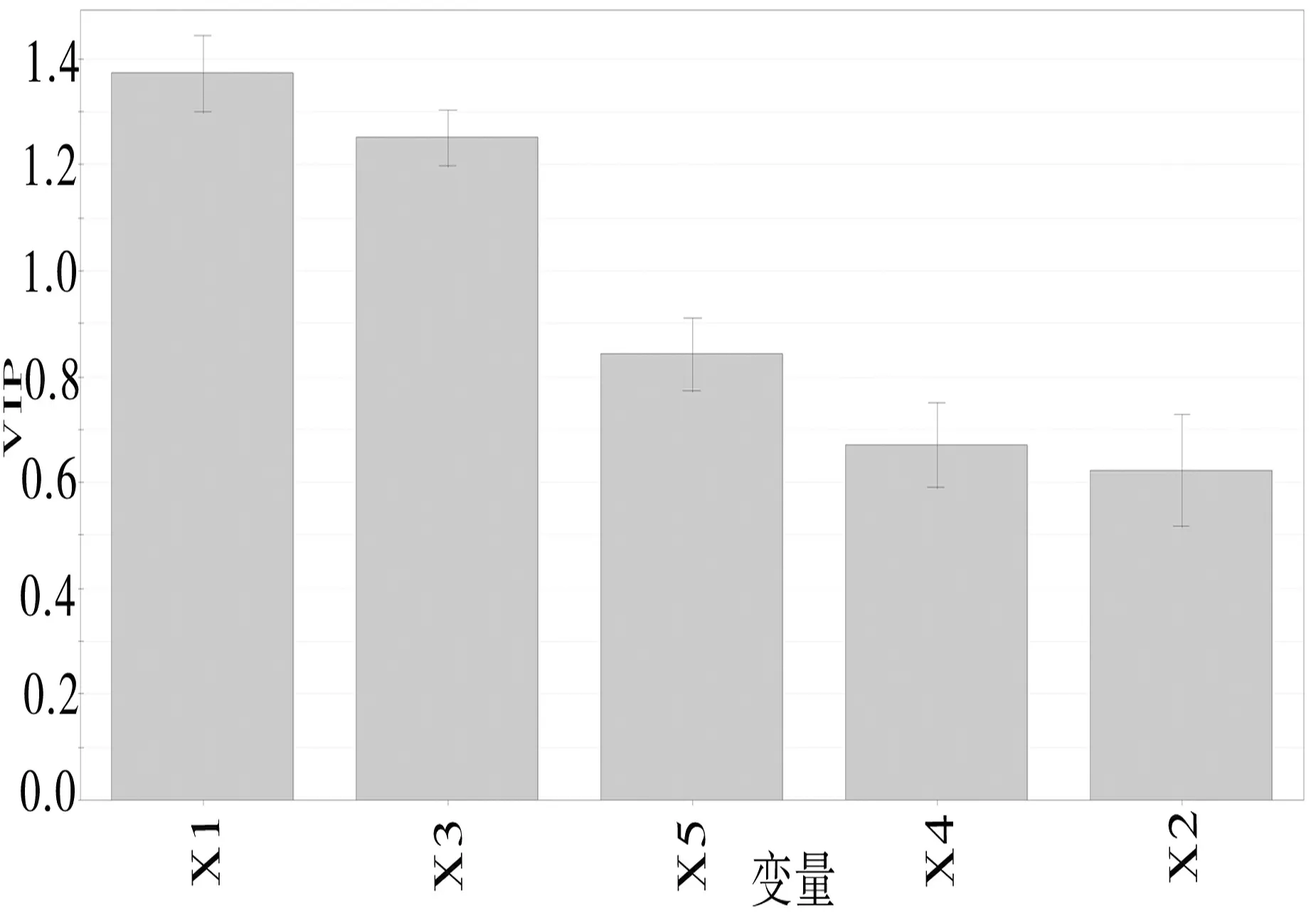
图6 VIP统计量图
结 论
本文首先在ARIMA模型对股票价格得出预测值的基础上,根据偏最小二乘方法在股票类数据的相关性消除方面的优势,引入ARIMA模型预测值作为因变量,再加入上一日交易量,上一日期货价格,上一日美元对人民币汇率,美国NASDAQ指数价格等变量,以上变量具有较强的相关性,通过偏最小二乘方法对其回归建模,能得到较好的修正模型,有效提高模型精度.
