改进小波阈值法与极限学习机在MEMS陀螺误差补偿中的应用

杨 辉,姜湖海,马 欣,毛 锐

(西南技术物理研究所,成都 610041)

微机械MEMS(Micro Electro Mechanical System)陀螺相对于挠性陀螺、激光陀螺、光纤陀螺等,具有体积小,重量轻,功耗低,成本低、启动速度快等优点,是弹载小型化低成本导引头测量角速度理想选择之一。但是,MEMS陀螺输出精度相对上述几类陀螺而言较差,随机漂移是影响陀螺精度的主要因素之一。目前主要有两种方法提高精度:一是提高加工工艺的精度,但周期较长且增加成本;二是数字精确补偿,后者相对而言更宜实施。

现有研究多采用数字滤波方法,文献[1]利用BP(Back Propagation)神经网络对三轴MEMS陀螺进行标定和补偿,在低转速区间上,神经网络的补偿效果比传统方法提高了3倍左右。Kalman滤波[2]因较好实时性得到广泛使用,文献[3]利用时间序列分析的建模方法和Kalman滤波技术,可以有效地减小MEMS陀螺的随机漂移误差,对提高MEMS陀螺的实际应用精度十分有益.文献[4]提出了一种多准则曲线辨识方法对 MEMS 陀螺的随机误差模型进行辨识。并在此基础上设计卡尔曼滤波器,对MEMS陀螺的测量输出进行随机误差补偿。文献[5]设计具有自回归滑动平均模型的自适应 Kalman滤波器,具有更广泛适用性,能够有效提高 MEMS 陀螺精度。Kalman滤波方法需建立准备的误差模型,而MEMS陀螺的随机漂移特性通常具有弱非线性、非平稳和慢时变,且极易受到外部环境等不确定因素的影响,导致Kalman滤波常因建模不准确导致滤波效果不理想。近年来,小波变换因其良好的时频分析特性和多分辨能力受到学者广泛关注,对改进小波阈值函数、求解最优门限阈值等方面作出大量的研究工作[6-7]。同时,在小波滤波算法的基础上文献[8]提出RBF(Radial Basis Function)神经网络模型对漂移误差进行建模补偿,文献[9]采用基于自回归滑动平均模型的Kalman滤波与支持向量回归机SVR(Support Vector Regression)预测补偿算法。人工智能算法建模补偿具有一定泛化能力,提高MEMS陀螺精度。而RBF神经网络当样本较少时,存在过学习问题,SVR并不能保证提供全局最优解。针对这些人工智能算法存在的不足,新加坡南洋理工大学黄光斌教授提出的一类基于随机隐节点神经网络算法[10-12]:极限学习机ELM(Extreme Learning Machine)。ELM克服其他算法收敛速度慢,易陷入局部极小等问题,以其强大的学习能力而在各领域得到广泛应用。

为此,本文提出采用改进后的小波阈值函数的小波去噪,结合ELM建模对MEMS陀螺随机误差进行预测补偿。

1 小波阈值去噪法

小波阈值去噪方法在保持信号奇异性的同时能有效地去除噪声,其基本思想是根据信号与噪声在各尺度上的小波系数具有不同特性的特点,按照一定的预定阈值处理小波系数,小于预定阈值的小波系数认定为由噪声引起的,直接置为零,大于预定阈值的小波系数认为主要是由有用信号引起的,直接保留下来(硬阈值法)或将其进行收缩(软阈值法),最后对得到的估计小波系数进行小波重构就可获得去噪后的信号。小波去噪流程[13]如下:①原始信号f(x)进行离散小波变换,得到一组小波系数wj,k,其中j为小波分解尺度;②在小波域对wj,k用阈值函数进行处理,得到小波变换系数Wj,k使得||Wj,k-wj,k||尽量小;③将Wj,k做离散小波反变换,得到f(x)滤波后信号F(x)。

常用的小波阈值函数可分为硬阈值和软阈值两种,硬阈值函数表达式为

(1)

软阈值函数表达式为

(2)

式中,λ为阈值。

硬阈值和软阈值方法已经实际中得到广泛应用,取得不错效果。但方法本身具有一定缺陷。硬阈值函数在阈值±λ点附近有阶跃现象,存在突变的情况。软阈值虽保持连续变化但与实际直线保持一个固定偏差。

1.1 改进阈值函数

本文引入新的阈值函数,其表达式为

Wj,k=

(3)

式中,a0、a0、b1、ω和β为参数。

分析式(3)可知,当β=0或β≠0且ω=0和a0+a1=0时,改进阈值函数等价于硬阈值函数;式(3)在硬阈值函数基础上增加在|Wj,k|∈[λ-β,λ]区间实现连续过渡。因此改进阈值函数在保留硬质函数优势前提下,克服软阈值固定偏差的缺陷,具备更灵活的处理效果。

设λ=4.5、β=2、a0=2.266 4、a1=-0.125 9、b1=2.234 2、ω=1.8,则绘制3种阈值函数估计小波系数如图1所示,图中改进阈值曲线在过渡区间实现连续平稳过渡,实现去燥后信号具有较好光滑性同时尽量保留原始信号特性。

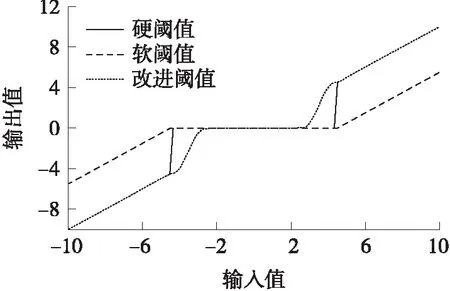
图1 3种阈值函数估计小波系数示意图

1.2 评价指标

为了定量分析改进阈值函数的性能,选择均方差MSE(Mean Squared Error)和信噪比SNR(Signal-to-Noise Ratio)两项指标衡量。MSE、SNR定义如下:

(4)

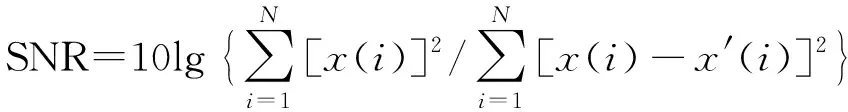
(5)

式中,x(i)、x′(i)分别为第i次去噪前后信号,N为信号样本数。同一信号中去噪处理后,MSE越小,SNR越大表明效果更优。

1.3 小波基函数与分解层数选择

小波阈值去燥法需要选择恰当的小波基函数和分解层数,根据支撑长度、对称性、消失矩、正则性和相似性等标准选择。本文参考上述标准,使用常见的基函数来处理实验数据,选择对应误差最小的小波基函数和分解层数。分析过程和结果详见下节。

1.4 试验对比

本文以某国产两轴MEMS陀螺为对象,该陀螺输出信号采样频率1 kHz。当设定转台速率值分别为0 °/s、±1.0 °/s、±2.0 °/s、±4.0 °/s、±5.0 °/s、±8.0 °/s、±10.0 °/s共13组速率值时,陀螺输出信号共104 567作为实验数据。

首先进行小波基函数与分解层数选择。提取转台速率为2.0 °/s时MEMS陀螺一轴输出信号共计361组数据进行计算,4种常用小波基函数在2层～8层分解情况下(均为软阈值),去噪效果MSE、SNR对比如表1所示。

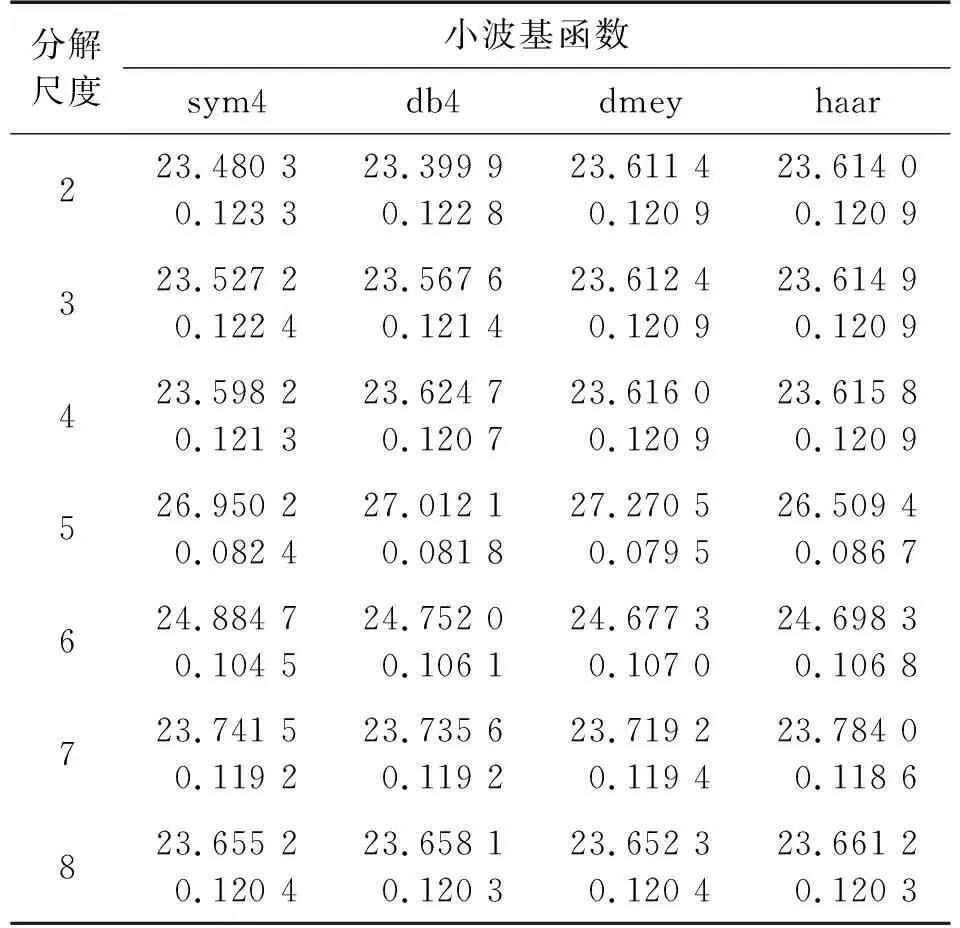
表1 4种小波分解层数去燥效果对比

表1中,评价指标SNR在上,MSE对在下。其中dmey基函数在5层指标最优,即降噪效果最好。因此,本文小波基函数采用dmey,分解层数选择5层。

由此,3种阈值函数去噪效果对比如表2所示。从评价指标MSE、SNR可知,改进后阈值函数去噪效果相对最优。因此,在采用改进小波阈值函数的小波去噪的基础上,下节将进一步讨论采用ELM进行随机误差补偿。

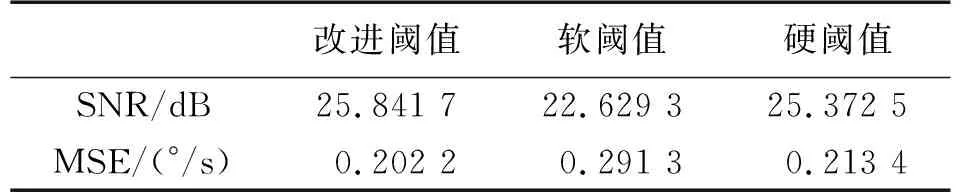
表2 阈值函数去噪效果比较

2 极限学习机建模

2.1 极限学习机训练原理

ELM训练采用前馈神经网络,结构如图2所示。其中,n、l、m分别为输入层、隐含层和输出层的节点数。wij表示输入层第i个神经元与隐含层第j个神经元间的输入权值,βjk表示隐含层第j个神经元与输出层第k个神经元间的输出权值。(xi,yi)为具有N个样本的训练集样本。

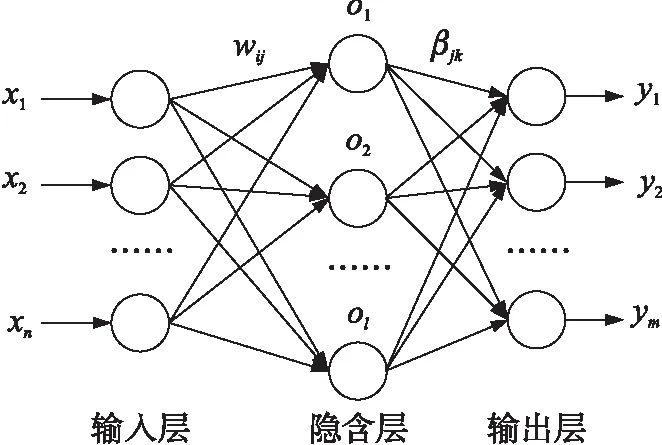
图2 极限学习机的神经网络训练模型

设隐含层神经元的阈值b为

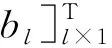
(6)

设隐含层神经元的激活函数为g(x),则网络的输出输出Oj表达式为

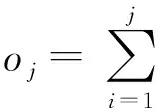
(7)

式中,wi=[wi1,wi2,…,win]。

ELM的代价函数E可表示为

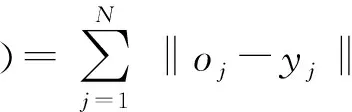
(8)

式中,S=(wi,bi),i=1,2,…,l,包含了网络输入权值及隐含节点阈值。ELM训练目标是求解最优S、β,使得网络输出值与实际值误差最小。

2.2 建模与结果分析

根据ELM训练原理,确定相关参数及样本等信息如表3所示。

表3 极限学习机相关参数统计

表2中,本文激活函数为sig,具有连续性、单调性,中心对称性等性质,是ELM常用激活函数之一。利用已建立的ELM模型,对测试样本进行随机误差补偿,其效果如图3所示。同时,对比改进小波阈值函数的小波去噪输出与ELM模型输出结果如图4所示,并计算评价指标MSE、SNR见表3。最后对相同样本采用BP神经网络建模,对比结果如表3所示。

图3 MEMS陀螺原始输出与ELM模型输出对比

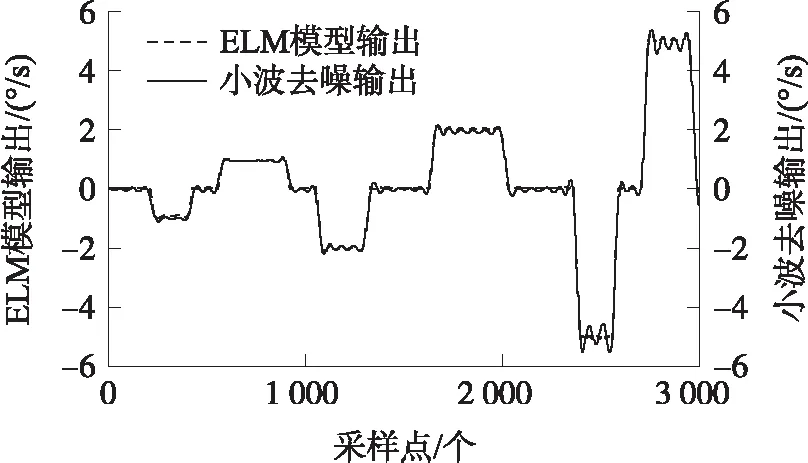
图4 ELM模型输出与小波去噪输出对比

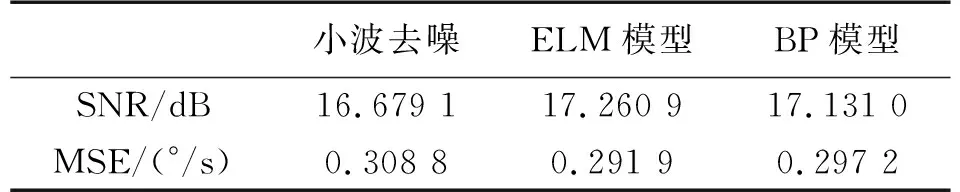
表4 ELM模型输出与小波去噪评价指标计算结果

观察图3、图4可知,本文方法在保证小波去噪的前提下,有效补偿MEMS陀螺随机误差,这种效果随着速率的增大而更加显著。例如,当转台速率为-5 °/s时,MEMS陀螺输出最大值和最小值为 -4.73 °/s、-5.27 °/s,对应本文方法输出最大最小各为-4.96 °/s,-5.05 °/s,说明本文方法对MEMS陀螺去噪及随机误差补偿均有效果。

表4进一步表明,将小波去噪与ELM模型结合可有效减小MEMS陀螺输出噪声,并提高精度。对比ELM与BP两种神经网络算法建模结果也同样论证ELM算法更优秀。

3 结论

针对MEMS陀螺精度较低的问题,本文提出一种新阈值函数的小波去噪与ELM建模的新方法,该方法采用改进阈值函数的小波去噪对MEMS陀螺原始输出数据进行滤波,提取有效信号作为ELM模型的输入向量,建立ELM模型。通过实例证明,将小波去噪和ELM相结合的MEMS陀螺随机误差补偿方法,比BP神经网络等算法有更好的补偿结果,具有一定的优越性,可应用于提高MEMS陀螺精度。