基于激光测距传感器校正四旋翼飞行器姿态的室内组合导航*

邹 强,付 超,莫申童

(1.天津大学微电子学院,天津 300072;2.天津市物联网国际联合研究中心,天津 300072)

由于惯性导航系统INS(Inertial Navigation System)陀螺仪、加速度计等传感器的自身测量误差,还会受到机体震动、温度等多方面影响,以致测量数据不精准[1]。同时,四旋翼飞行器在室外环境下,可以借助INS与全球定位系统GPS(Global Position System)实现自主导航[2],但在室内环境下,无法利用GPS实现精准定位,因此需要可行的导航技术,实现室内精准导航。

采用更优的算法或多传感器融合是研究方向之一,即在原有惯性测量传感器的基础上融合更多姿态传感器的姿态信息,选择最优的在线数据融合策略,从而得到最优的组合导航[3-4]。文献[5]利用二维激光雷达和惯性导航系统构成微小型无人机MAV(Micro Aerial Vehicle)室内组合导航方案,采用基于扩展卡尔曼滤波(EKF)的D&C同步定位与构图技术(SLAM)实现定位和构图;文献[6]How等使用单目视觉对室内环境进行角点特征提取,根据角点匹配执行基于扩展卡尔曼滤波EKF(Extended Kalman Filter)的SLAM算法(EKF SLAM),得到MAV的位置估计,同时构造一个低精度的3D地图。虽然EKF执行效率很高,但是图像处理运算量较大,无法满足MAV对导航的实时性要求;文献[7]Bachrach等提出了一种大范围室内导航方案。该方案以二维激光雷达为传感器,采用基于粒子滤波器PF(Particle Filter)的GMapping算法进行定位,具有较高的定位精度,但是PF-SLAM的耗时较长,也无法满足MAV对导航的实时性要求;文献[8]Grzonka等在MAV的室内导航方案中使用惯性测量模块直接输出姿态角,但并未充分利用速度进行组合滤波,无法保证长时间的导航精度;文献[9]Adam Bry等为了对攻击性飞行提供精确的状态估计,将高斯粒子滤波器扩展到允许将激光测距传感器定位与卡尔曼滤波器相结合;文献[10]针对室内定位,文献提出了一种融合可视光通信和基于粒子滤波器的惯性导航的融合定位系统,与传统惯性导航相比,此融合系统定位精度要提高2倍～4倍;文献[11]提出了一种共轭梯度优化方法与互补滤波相结合的数据融合策略,克服了梯度下降法的不足,弥补了牛顿法计算量大的缺点;文献[12]针对显示互补滤波中PI参数只能试凑的问题,提出了自适应显示互补滤波,实时调整PI参数,提高了姿态估计的精度。

本文提出一种基于激光测距传感器校正四旋翼飞行器姿态的室内组合导航,在短时间内依靠INS系统,长时间内通过激光测距传感器校正姿态,通过激光测距传感器所测数据进行数学变换来估算飞行器的姿态参数,将所估算的姿态参数与经过互补滤波后的姿态数据通过扩展卡尔曼滤波融合,该室内组合导航结合了互补滤波与扩展卡尔曼滤波的优点,在静态时能够抑制姿态角漂移和滤出噪声,动态时能够快速跟踪姿态的变化,提高了姿态角的解算精度。本文详细给出了上述方法的实现过程,并通过实验验证了方法的有效性。

1 姿态角的描述

四旋翼飞行器的坐标系由机体坐标系和地理坐标系组成,两者关系如图1所示。

图1 地理坐标系与机体坐标系的相对关系

机体坐标系与地理坐标系的原点重合,由欧拉旋转定理,通过三次依次围绕机体坐标系x、y、z轴的旋转可以使机体坐标系与地理坐标系重合,其中绕机体坐标系x、y、z轴旋转的角度分别为横滚角φ、俯仰角θ、偏航角ψ。

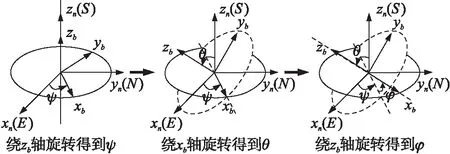
图2 三次坐标旋转得到欧拉角

按照z-y-x的旋转顺序转换坐标系,得到如下的姿态旋转矩阵:

R=

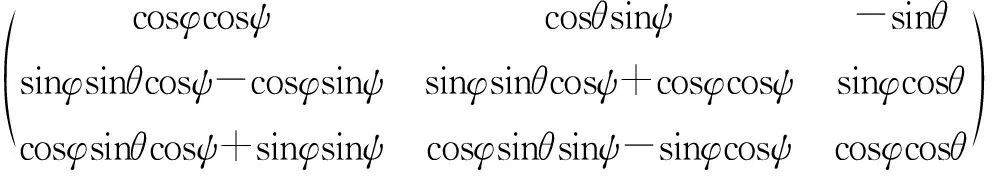
(1)

由公式可以看出,由欧拉角方法表示的姿态矩阵直观,计算简单,但会出现奇异性问题,不能够全姿态运行,因此还需要其他的表示方法。

2 四元数姿态解算

描述姿态旋转,除了欧拉角方法,还有方向余弦矩阵、四元数等,方向余弦法的姿态微分矩阵方程中包含了9个未知参数,计算量大,实时性困难;而四元数描述方法包含了四轴飞行器所有的姿态信息,有效的避免了奇异性问题,而且只有4个未知数,方程解算简单,是目前四轴飞行器采用最广泛的方式。

四元数(Quaternions)是由爱尔兰数学家哈密顿(William Rowan Hamilton,1805-1865)在1843年发明的数学概念。四元数由4个元组成,其复数形式为:

Q=q0+q1i+q2j+q3k=[q0q1q2q3]T

(2)

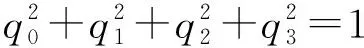
通过四元数推导得到由机体坐标系(b系)到地理坐标系(n系)的旋转矩阵为:

(3)

对比姿态描述矩阵式(2)与式(3),可以得到四元数与欧拉角的对应关系:

(4)

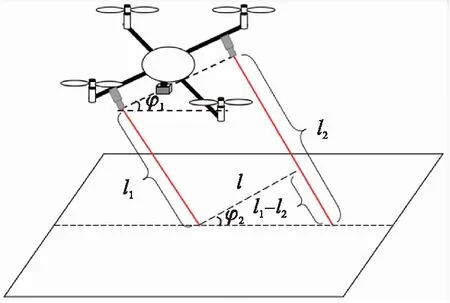
图3 标准飞行下激光测距传感器获取姿态角原理图

3 激光测距传感器校正姿态参数的混合滤波算法

3.1 激光测距传感器混合滤波算法的基本思路

激光测距传感器的抗干扰性强于陀螺仪、加速度计以及磁力计等惯性传感器,光信号不含或含有少量的噪音,不需要设计专用的数字滤波器。陀螺仪具有良好的动态特性,产生的数据含有低频噪音;而加速度计和磁力计具有良好的静态特性,产生的数据含有高频噪音。因此通过互补滤波分别设置高通滤波器和低通滤波器滤除低频和高频干扰,方便融合3个传感器,提高测量精度和动态特性。激光测距传感器获取四轴飞行器相对地面的感知,经过解算之后得到飞行器的姿态参数,再通过扩展卡尔曼滤波算法,将激光测距传感器与惯性传感器的数据融合,得到更为精确的导航信息。

3.2 激光测距传感器测量飞行模型

3.2.1 四旋翼飞行器水平标准飞行

激光测距传感器测量得到距离参数l1、l2,而两个激光测距传感器之间的距离l已知,得姿态角计算公式:

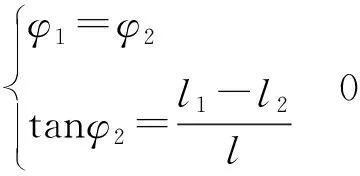
(5)

3.2.2 四旋翼飞行器倾斜横动/纵动飞行

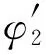
(6)

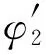
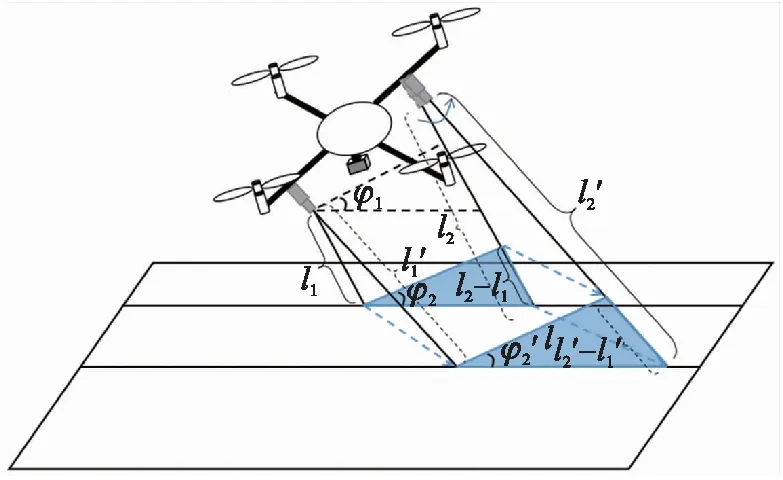
图4 倾斜横动/纵动飞行下激光测距传感器获取姿态角原理图

3.2.3 误差校准

图5为图4的右视图,如下所示。

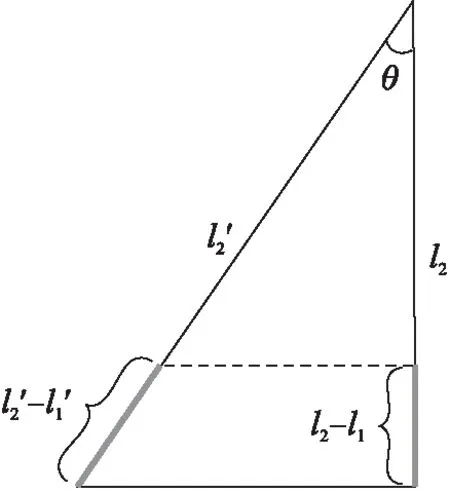
图5 俯仰角θ大小与l2′-l1′关系l2′-l1′

由于飞行模型复杂,本文采用

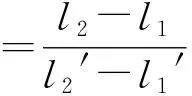
(7)

式中激光测距参数与俯仰角的关系来粗略校准。

图6为四旋翼飞行器飞行模型全姿态示意图,激光测距传感器在具有稳态误差的基础上进行测量,测量后的数据需要再校准后才能得到真实的姿态角。

激光测距传感器得到修正后的横滚角速度、俯仰角、偏航角数据,对其微分,得到角速度wl。

3.3 基于扩展卡尔曼滤波算法融合INS与激光测距传感器数据

激光测距校正姿态角的互补滤波与卡尔曼滤波混合算法示意图如图7所示。

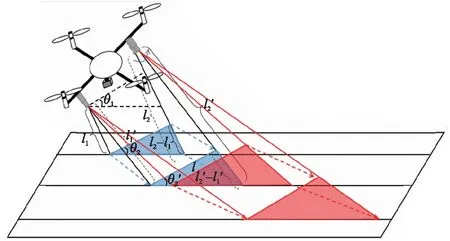
图6 四旋翼飞行器飞行模型全姿态示意图

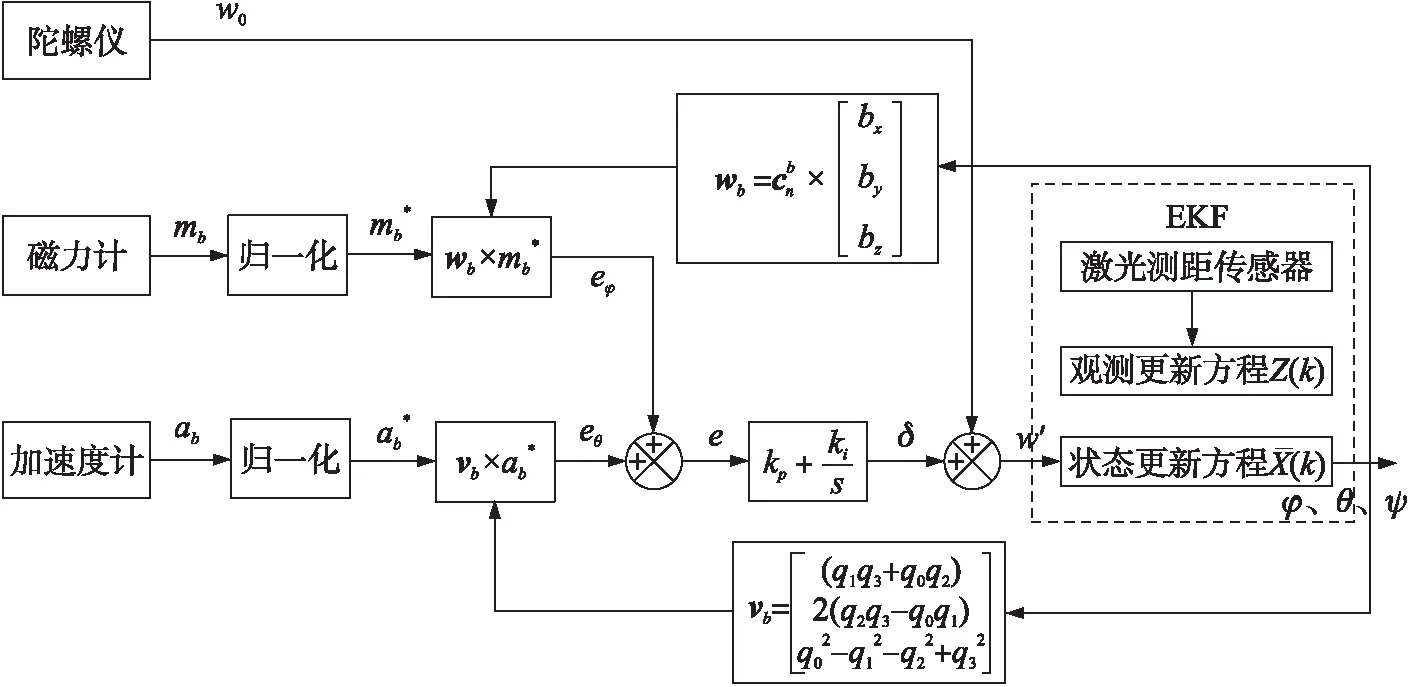
图7 激光测距校正互补滤波与扩展卡尔曼滤波混合算法流程图

将姿态向量误差e输入到PI控制器与陀螺仪测量的角速度数据相融合,得到经过加速度计和磁力计修正过的角速度ω′为:

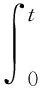
(8)

姿态四元数为状态量的卡尔曼滤波状态方程是非线性的,因此在无人机飞控系统的数字处理器中主要采用扩展卡尔曼滤波算法。

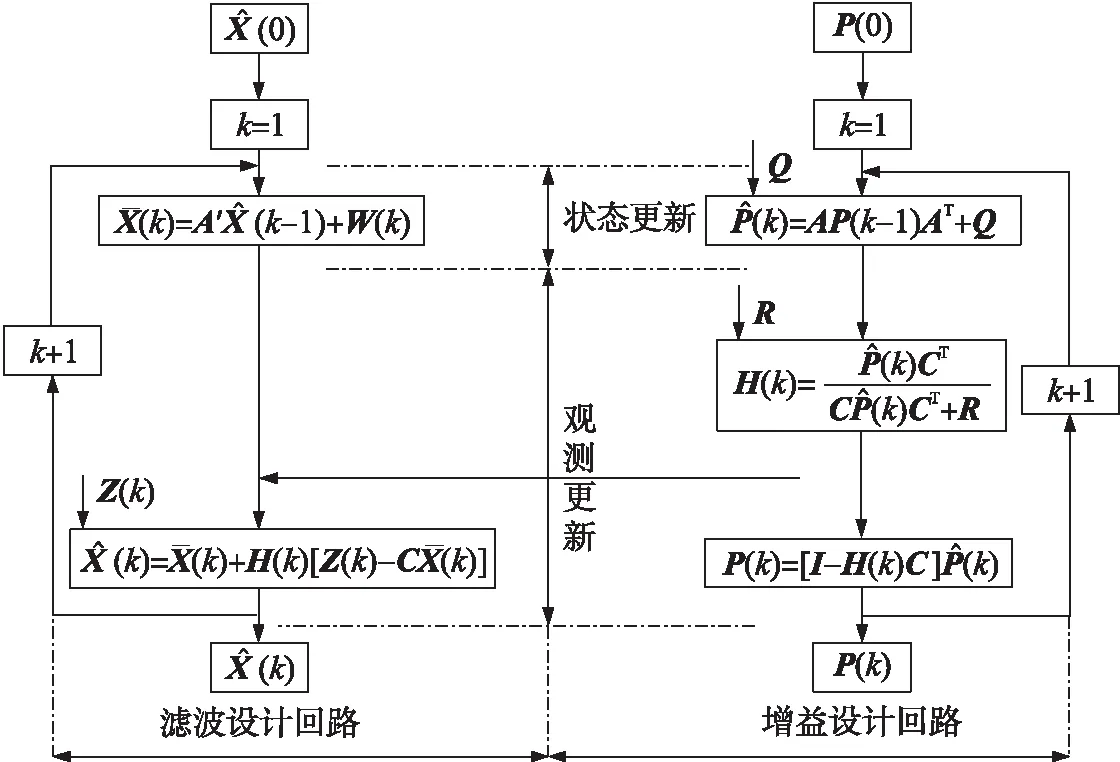
图8 扩展卡尔曼滤波算法预测更新流程图

通过扩展卡尔曼滤波将激光测距传感器得到的角速度wl与INS的角速度w′融合。

EKF的预测更新流程图如图8所示。

用INS的输出计算四元数关于时间的离散状态方程:

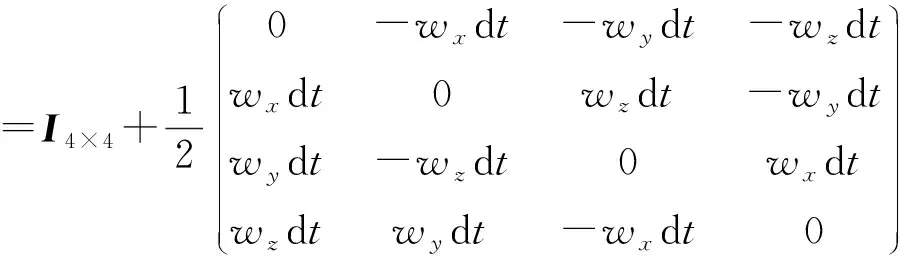
(9)

则时间更新方程为:

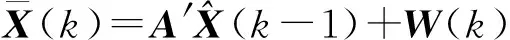
(10)

进行下一时刻的数据测量,读入激光测距传感器观测值,即观测更新方程Z(k):

以z轴为参考系,则激光测距传感器以地理坐标系为参考的角速度矢量:

wl=(wnxwny0)T

(11)

在机体坐标系中,激光测距传感器的测量值为:

wb=(wbxwbywbz)T

(12)

因为标准角速度向量无法测量,将式(12)转换到地理坐标系n系,得到预测角速度向量:

hn=(hxhyhz)T

(13)

式(11)与(13)有以下关系:

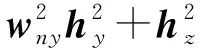
(14)

当机体处于静止或匀速直线运动时,以上空间向量满足如下关系:

(15)

以式(12)为测量模型,测量值为6个激光测距传感器组成的3轴角速度数据,展开如下:

(16)

(3)读入四元数的数据,根据式

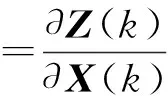
(17)

计算C′矩阵。

根据式

(18)

(19)

得到此时的滤波增益矩阵H(k)。

根据式

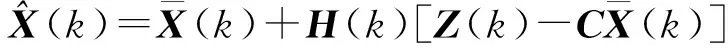
(20)

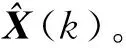
根据式

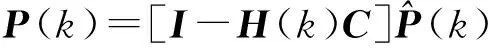
(21)

计算下一时刻的协方差P(k),当系统进入k+1状态时,P(k)就是式(18)的P(k-1),这样卡尔曼滤波算法就可以自回归的运算下去。

经过扩展卡尔曼滤波后四元数旋转矩阵得到修正,代入到式(4)中,求解出横滚角φ、俯仰角θ、偏航角ψ。

4 实验与结果

4.1 姿态解算实验测试平台

本节简单介绍姿态解算实验平台,在实验平台上检测带有激光测距传感器及惯性系统的组合导航的静态特性、水平滑动和动态特性。

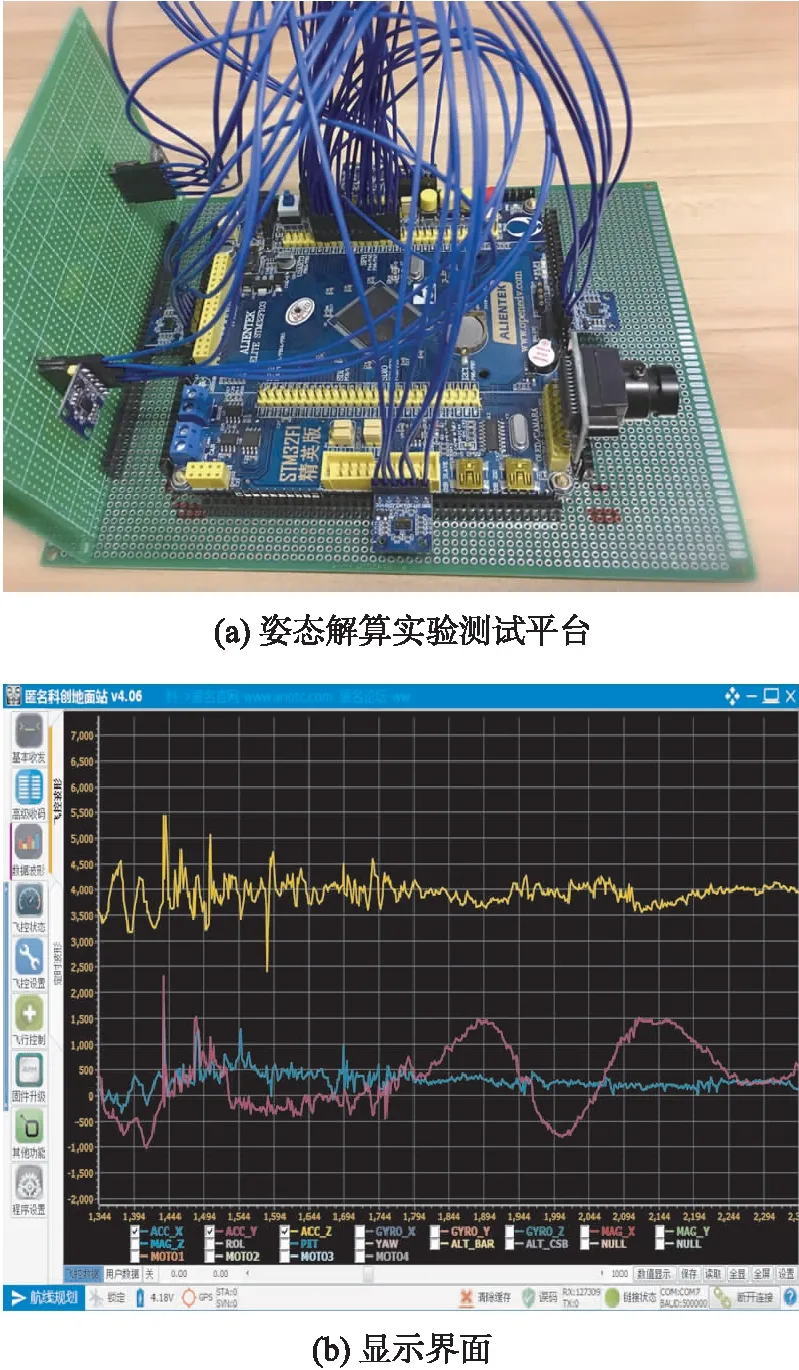
图9 姿态解算实验测试平台与显示界面

实验平台采用ALIENTEK开发板,主控制器采用STM32F103进行数据处理,姿态传感器由MPU6050(三轴陀螺仪和三轴加速度计)和三轴电子罗盘HMC5883L组成,用于采集机体角速度、加速度以及磁场强度数据,姿态校正传感器由6个激光测距传感器组成,激光测距采用的是ST公司的VL53L0X模块,用于测量机体的姿态角,在高速模式下,采样频率为50 Hz。为保证水平,在采样前需要对激光测距传感器进行校准。显示界面采用匿名四轴上位机。

4.2 实验结果与分析

姿态解算时,姿态传感器模块MPU6050、HMC5883L以及激光测距模块通过I2C协议实现与主控制器之间的通信,主控制器获取实时的加速度、角速度以及磁场强度数据进行姿态解算得到相对准确的角速度值,再由激光测距模块对该角速度值进行校正,最终获得姿态角数据,通过串口调试助手发送到上位机中,可显示激光测距传感器、陀螺仪等的测量数据和姿态角波形,并可将测量数据导出到EXCEL中进一步分析。

4.2.1 静态测试

将姿态解算实验平台置于水平台面上,理想的横滚角应该为0°。当姿态解算平台处于静止时,单独使用加速度计时输出的横滚角如图10(a)所示,在5 s内最大误差在0.35以内。使用陀螺仪时(修正后)输出的横滚角如图10(b)所示,在5 s内最大误差在0.18以内。而单独使用激光测距传感器时,实验平台输出的横滚角在5 s内静态误差基本控制在0.05附近,成一条水平的直线。由此可以得出结论,激光测距传感器在静态测试中具有较好的滤除作用。

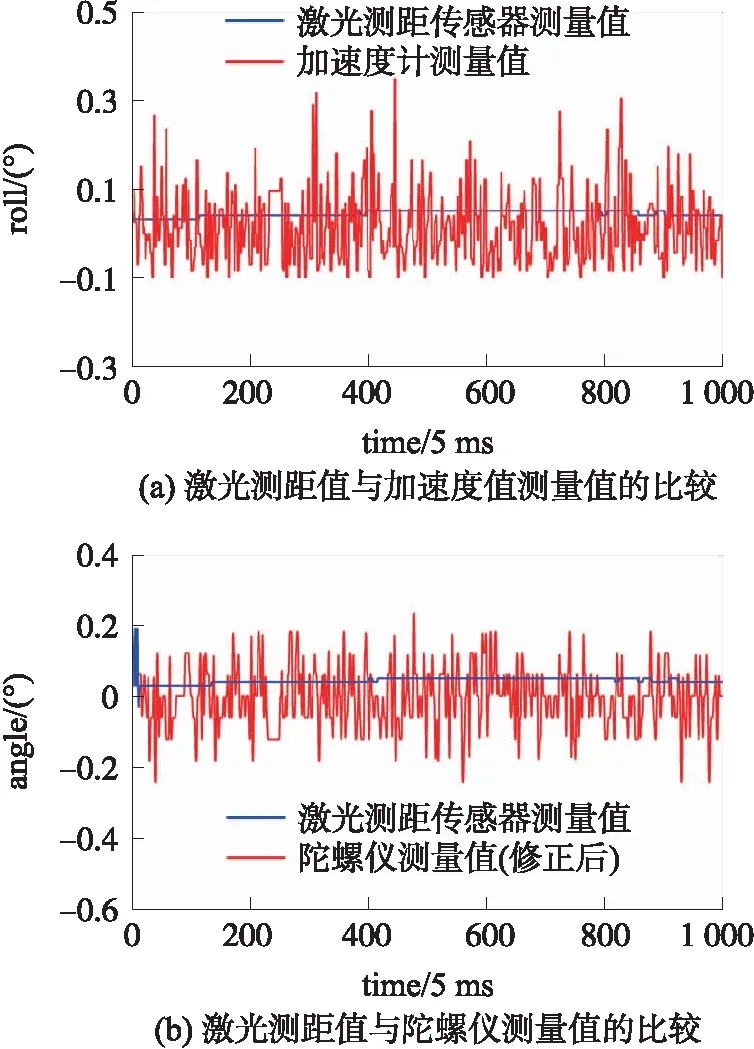
图10 静态测试横滚角估计

4.2.2 水平滑动

针对加速度无法区分运动加速度和重力加速度,激光测距传感器工作原理能够区分运动加速度和重力加速度,因此本文设计水平滑动实验,将姿态解算平台放置在水平桌面上做快速滑动处理,理论上俯仰角和横滚角输出角度为0°,但INS系统下,横滚角误差达到了22°左右。经过本文设计的激光测距传感器校正姿态后,误差控制在7°。实验验证了水平滑动状态下,激光测距校正加速度数据缺陷的有效性。

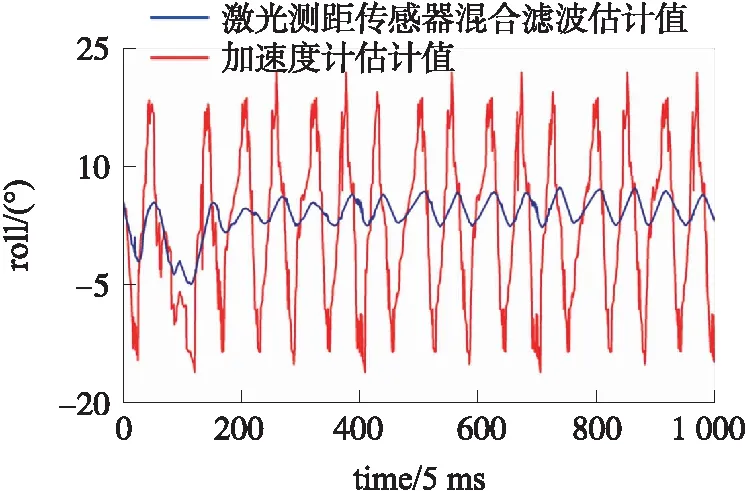
图11 水平滑动测试横滚角估计

4.2.3 动态测试

动态测试分为姿态变化较慢与姿态变化较快两种情况,5 s内采用激光测距传感器校正四旋翼飞行器姿态的混合滤波算法(以下简称激光测距混合滤波算法)后的横滚角曲线如图12所示。

从图12可以看出,姿态变化较慢时采用激光测距混合滤波算法后的姿态角曲线更加平稳,产生的波动较小,横滚角偏差最大值不超过1°。实验结果表明,激光测距混合滤波算法能够有效的修正陀螺仪的漂移特性而产生的积分累积误差,提高姿态解算的精度。

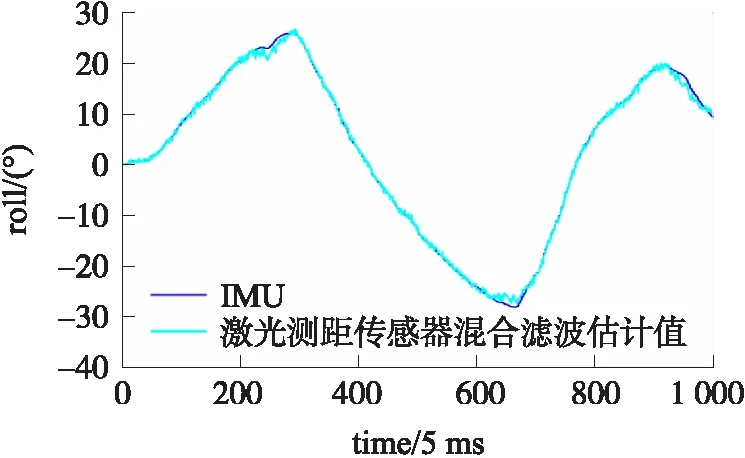
图12 姿态变化较慢时横滚角估计

但当运动角度过大时,如图13所示,激光测距组合导航系统产生的误差逐渐增大,这是由于激光测距自身性能限制,角度过大时,激光测距接收器不能接收所发射的光子,采用性能好的激光测距传感器会避免这一点。同时,由于本文激光测距测量数据修正方法较为粗略,对误差有一定的影响。

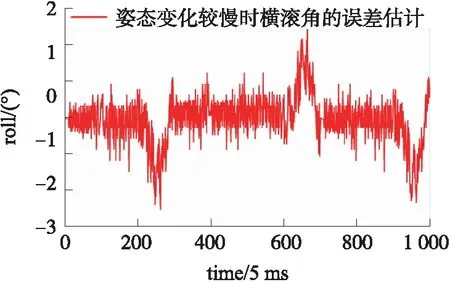
图13 姿态变化较慢时横滚角误差估计

为进一步验证基于激光测距混合滤波算法的有效性,本文模拟了姿态变化剧烈的情况。如图14所示,在平稳阶段,激光测距混合滤波算法几乎没有延迟,能够很好地实现姿态的跟踪。在姿态变化剧烈的时候,采用激光测距混合滤波算法有一定的延迟,与采用扩展卡尔曼滤波方式有关。

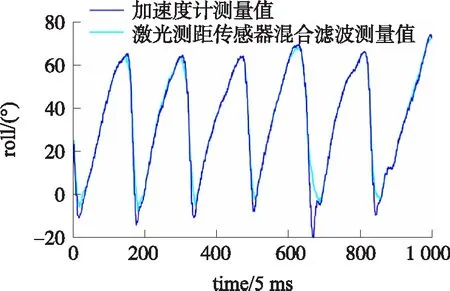
图14 姿态变化剧烈时横滚角估计对比图

5 总结

本文针对室内环境下无法使用GPS实现精准导航的问题,提出一种基于激光测距传感器校正四旋翼飞行器姿态的组合导航,并结合姿态解算算法建立了姿态解算实验测试平台,对该组合方式进行实验验证。实验结果表明,基于激光测距传感器校正姿态组合导航算法,能够使姿态解算平台具有较好的静态特性、水平滑动和动态特性,有效的修正陀螺仪的漂移特性而产生的积分累积误差,提高了导航的精度,而且满足姿态解算的实时性,但由于激光测距传感器测量姿态原理自身缺陷造成角度过大时误差增大,还需要进一步研究优化,修正误差,而且仅限用于室内环境下。激光测距传感器组合导航对未来将激光测距传感器单独作为姿态解算传感器做了基础性研究,有较好的工程应用前景。