基于短时客流预测的地铁动态限流预警模型研究
2018-11-02杨安安陈艳艳黄建玲王少华
杨安安 陈艳艳 黄建玲 熊 杰 王少华
(北京工业大学北京市交通工程重点实验室,100124,北京//第一作者,博士研究生)
北京地铁客流近年来屡创新高。根据北京地铁运营公司2016年4月数据,全网客流逼近1 270万人次。目前北京常态化限流站点总数达75座,即超20%的站点实施常规限流。实施限流时,一般为工作人员根据站台客流密度的变化情况,引导乘客分批进入来实施。由此可见,现有的限流措施多基于车站工作人员的主观感受和经验判断,缺少事前预警,以事中控制为主。
车站限流(也称客流控制)方面研究主要有:文献[1]从轨道交通的运营能力角度出发,提出了站点超大客流管控线性规划模型;文献[2]以上海轨道交通某站为例,根据车站服务设施的负荷情况制定了针对性的限流组织方案;文献[3]提出车站间限流安全控制的实施方式,并分析了车站单点、线路和路网上的协同限流方法;文献[4]基于数学规划方法分别建立了适用于线路层和网络层的客流流入协同控制模型。客流预警方面研究有:文献[5]研究了闸机客流、通道客流、站台客流等多因素之间的关联预警分析流程,并基于系统动力学(SD)原理建立了车站客流流动模型;文献[6]用ARMA模型在轨道交通客流预测基础上进行预警;文献[7]对地铁客流预警技术基础进行了探讨。
可见与限流相关的研究主要关注限流组织方法、控制方式,以及协同控制模型的推导。大客流预警方面的研究,多是围绕预警机制以及级别划分与判定等预警基础技术的分析与探讨,虽也有预测基础上的预警判断,但在应用层面上缺少系统的、量化的限流参数的分析。基于此,笔者将短时预测与限流预警相结合,按照预测-预警-限流实施方案的思路,在用小波神经网络进行短时客流预测的基础上,对比列车的剩余运力再结合关键设备设施的限流阈值来制定具体的动态限流预警方案。
1 限流特性分析与阈值判断
1.1 限流特性分析
客流在站点设施上的分布随时间和空间发生动态变化,本文认为站台是决定限流的关键设施,原因如下:①所处位置——站台是站内出行终端设施,等候上车的乘客在此聚集,列车到达离开客流才能疏散,一旦聚集等候的客流达到站台容纳能力时,则需要考虑限流;②功能上——上下车以及换乘客流这3股客流在站台交叉混合,流线冲突最多;③安全性——站台边缘是轨道设施,人群拥挤摩擦下很可能发生挤门、冲门、吊门,若无安全门还有可能发生坠轨等危险事件,站台的安全隐患问题较为突出。因此,本文研究的限流目标是控制站台滞留人数。
从时间上分析,站台人数随着乘客进站,以及列车的到达与发送而发生周期性的动态变化。高峰时段大量客流进入站内,列车剩余运力有限,部分乘客滞留在站台上,当滞留总数达到阈值时,开始实施限流;通过控制、限制客流进站速率,站内滞留人数保持在阈值以下,客流被限制在站外,故站外逐渐形成排队客流。客流高峰过去后,随着进站客流减少,排队从最大队长直至消散,限流结束。
1.2 阈值判断
站点限流预警目前在国内外尚无公认的阈值定义,研究最为广泛的是客流密度值。人流密度是人群密集程度的定量表示,反映一个空间内人群的稠密程度,一般用单位面积上人员的数量表示,单位为人/m2。
国际上常采用文献[8]人员密度服务水平评价指标,该研究形成了有价值的人员行动能力和空间几何尺寸的数据资料,该资料表明当人流密度达到1.43~3.33人/m2时,人群行动能力就会受到严重限制。文献[9]整理出了一组人流密度和行进速度关系曲线,国内文献[10]对地铁站台集散区人流密度与速度关系进行了研究,并得出当站台集散区的客流密度达到2人/m2时, 乘客的行进速度极其缓慢的结论。另外,文献[11]指出,当通道内密度达2人/m2时,人立即会产生拥挤的感觉。
据广州地铁的客流组织经验,站台能安全容纳乘客的数量一般为2~4人/m2。文献[7]经过在北京地铁的实际调研,认为2人/m2作为拥挤阈值的预警比较合理。综上所述,本文拟采用站台滞留人数的客流密度达2人/m2作为北京某站点算例的限流阈值进行计算。
2 限流预警模型构建
2.1 假设
由于简化问题的需要,本文做如下假设:
(1) 因对实时进出站客流难以区分其上下行方向客流所占比例,故本模型假设上下行方向的进出站客流一致,不加以区分;
(2)模型假设高峰时车内乘客数量保持最大满载状态,其值等于列车定员乘以超员率(一般取120%~130%)。
2.2 建模
模型的基本约束条件:站台滞留人数小于等于限流阈值。
(1) 第i周期站台滞留人数L(i)
直接影响因素包括进站候车客流、上车客流;通过短时预测可得的已知量,即预测的进出站客流。
乘客从进站到站台候车,以及下车到出站都需要一定的步行时间。为了清楚地表达闸机记录的进出站客流、站台等待候车与下车客流的时间差异关系,定义进站到站台候车耗时n个周期,下车到出站耗时m个周期。
Win(i)=Qin(i-n)
(1)
qoff(i)=Qout(i+m)
(2)
式中:
Win——第i周期进入站台的候车客流;
Qin(i-n)——第i-n周期该站的进站客流,为进站闸机采集的刷卡数据;
qoff(i)——第i周期内在本站的下车人数;
Qout(i+m)——第i+m周期该站的出站客流,为出站闸机采集的刷卡数据。
若该站为换乘车站,因换乘线路的存在,换乘客流与该线客流交叉混合,此时Win(i)和qoff(i)的组成则复杂得多,具体如下:
Win(i)=Qin(i-n)-Qin,tr(i-n)+Cfr(i)
(3)
qoff(i)=Qout(i+m)-Qout,tr(i+m)+Cto(i)
(4)
式中:
Qin,tr(i-n)——第i周期进站客流中去往换乘线路的客流;
Cfr(i)——第i周期通过站内换乘至本线路的客流;
Qout,tr(i+m)——第i+m周期出站客流中来自换乘线路的客流;
Cto(i)——第i周期本线路换乘至换乘线的客流。
站台滞留人数的另一个直接影响因素——第i周期上车客流qon(i),与列车的剩余运力A(i)(也是直接疏散站台候车客流的能力)紧密相关,A(i)的计算模型如下:
A(i)=Nmaxt/T-P(i)+qoff(i)
(5)
Nmax=Nβmax
(6)
P(i)=F(i)·T
(7)
式中:
t——一个计算周期的时间间隔;
P(i)——列车到达时实际载客量;
Nmax——列车最大定员;
N——列车定员;
βmax——最大满载率;
F(i)——该站与该线路上一站的断面在单位时间内通过的客流。
需要说明的是,断面流量F(i)与全网流量有关,可通过网络客流分配得到。对于换乘车站,换乘客流Cfr(i)、Cto(i)、Qin,tr(i-n)与Qout,tr(i+m)直接采集较难,可借助于换乘客流监测系统来实现。
上车客流qon(i)与列车的剩余运力A(i)关系如下:
qon(i)=min{Win(i),A(i)}
(8)
第i周期站台预测滞留人数L(i),为进站候车客流与上车客流预测值之差,同时将上个周期实际值与预测值的偏差对预测的滞留人数进行修正:
(9)
式中:


(2)限流开始时间Ts
定义预测到连续2个周期的站台滞留人数均达到限流阈值R,就开始限流。
Ln1=R,Ln1+1=R
(10)
R=cS
(11)

(12)
Ts=n1t+T1
(13)
式中:
n1——开始限流的时间周期;
c——站台单位面积限流阈值,人/m2;
S——站台有效面积,m2;
a——站台长度,m;
b——站台宽度,m;

Ts——限流开始时间;
T1——该站点开始运营时间。
(3)限流流率B(i)
限流流率即该站点单位时间内控制进入的客流量,当站台已处于限流阈值这种饱和状态时,为了使站台滞留人数不再增加,此后进站客流流率与列车剩余运力必须保持一致。
B(i)=A(i)/t=(Nmaxt/T-Pi+qoff(i))/t
(14)
式中:
T——列车发车时间间隔。
(4)站外最长排队人数G
定义到第n2个周期时,进站客流持续减少,当与列车运力相同时,站外排队为最长,即:
(15)
需要说明的是,第n2周期之后,虽然进站候车人数减少,且小于车辆运能A(i),因为排队人数的存在,上车人数qon(i)=A(i)。
(5)限流结束时间Tf
定义到第n3个周期时,进站口无排队,限流结束,即:
(16)
式中:
Tf——限流结束时间。
3 算例分析
选取北京地铁十号线某站点作为算例进行限流方案分析,该站5:00开始运营,高峰小时(7:30—8:30)进站客流高达6 800人次,列车满载率较高,乘客上车困难,站内拥挤。
本文所使用的数据来自于地铁自动售检票(AFC)系统记录的乘客刷卡数据,试验数据为2015年8月25日至28日,分别为周一至周四的上午(5:00—12:00)进出站客流数据。采集间隔为5 min,数据量为336条。取精度较高的数据作为下一步限流预警方案的数据基础。
3.1 运用小波神经网络进行短时预测
客流预测算法首先对2015年8月25日至27日的进站客流、出站客流进行训练学习,然后预测8月28日(5:00—12:00)的进站客流、出站客流,并与实际客流数据进行对比评价。算法根据小波神经网络原理并采用软件MATLAB编程实现。
通过设置不同的网络结构经过多次训练,最终采用误差最小的网络结构。本算例中进站客流预测采用4-6-1结构:即输入层有4个节点,表示预测时间节点前4个时间点的交通流量;隐含层有6个节点;输出层有1个节点,为训练的网络预测的客流量。出站客流预测采用4-8-1结构。随机初始化小波函数的伸缩因子、平移因子以及网络连接权重,设置网络学习速率为0.01,训练1 000次。预测结果如图1所示。
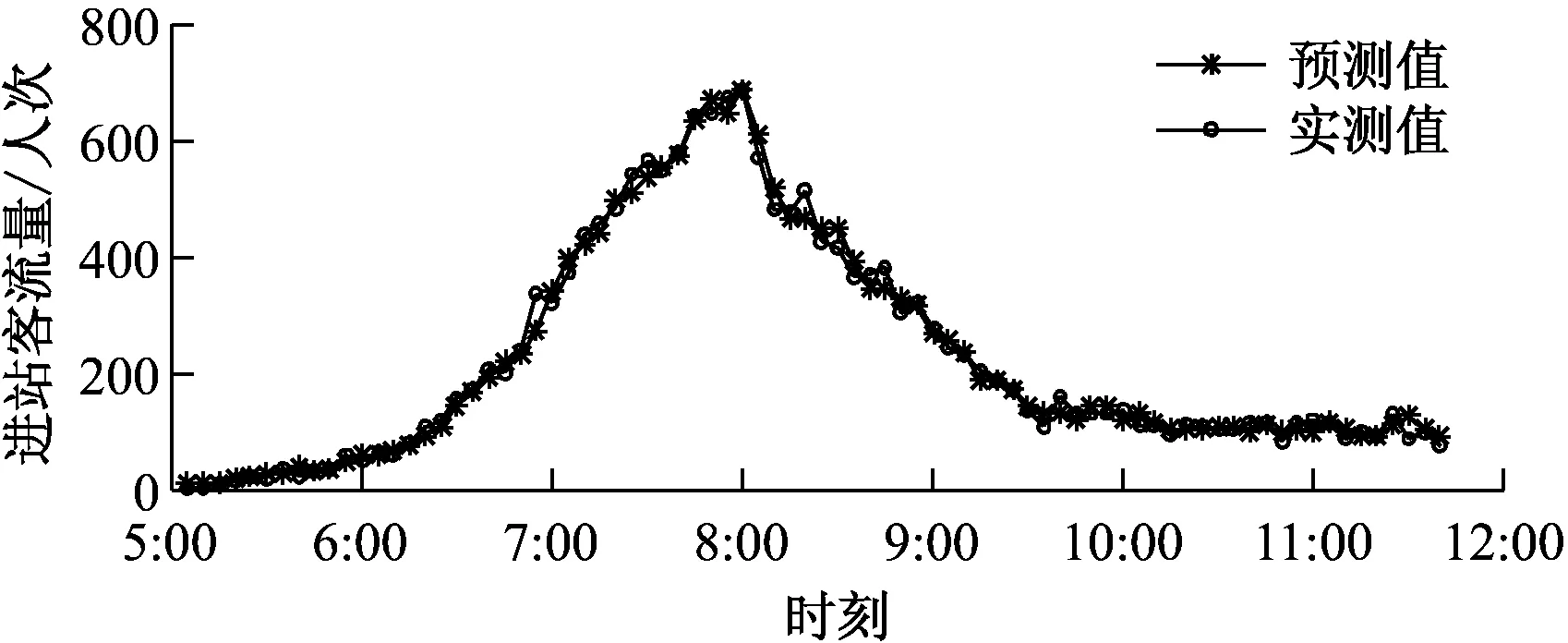
a)进站
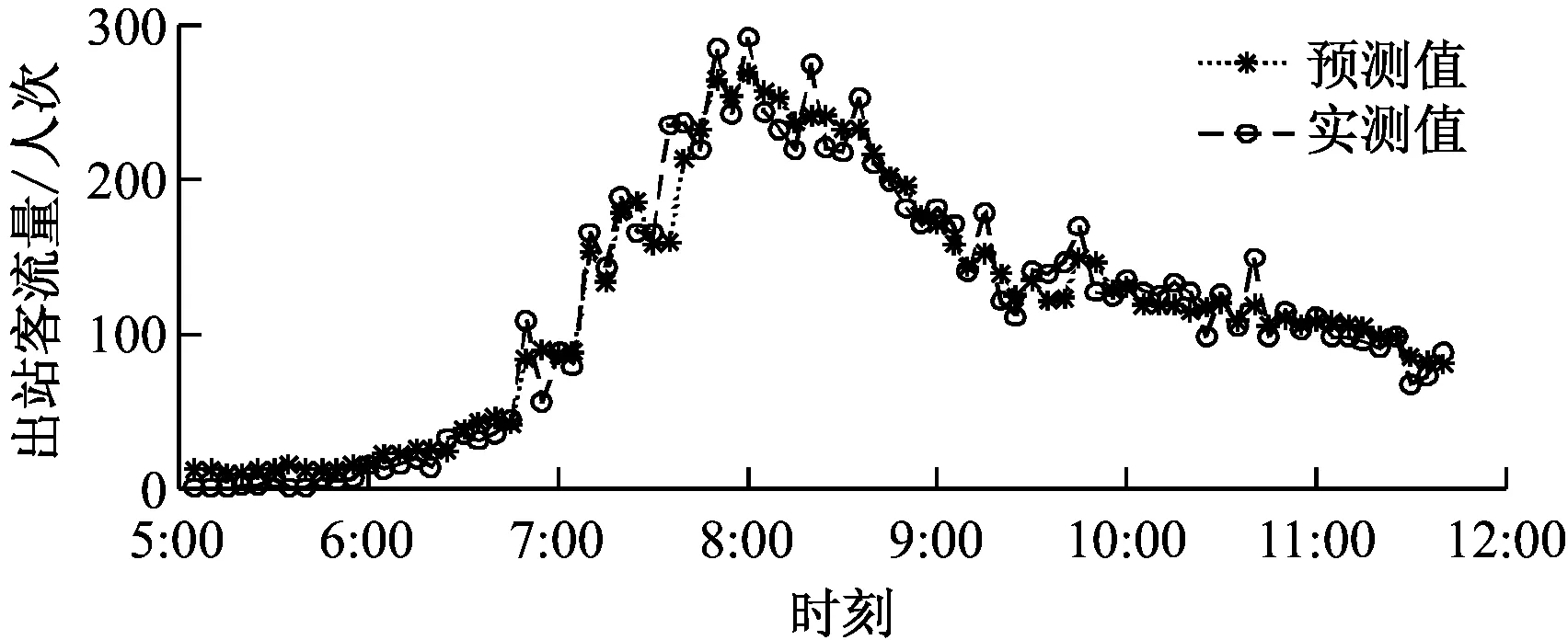
b)出站图1 预测进、出站客流与实测值比较
从图1结果可以看出,输出层的预测值和实测值变化趋势基本保持一致。本文使用以下3个指标比较早高峰(7:30—9:30)的预测精度。
(1)平均相对误差
式中:

Y(t)——实测值。
(2) 最大相对误差
(3) 拟合度
出站客流主要受列车到发影响,数值波动性更强,平稳性较差。从表1计算结果也可看出,出站客流预测精度明显低于进站客流精度。
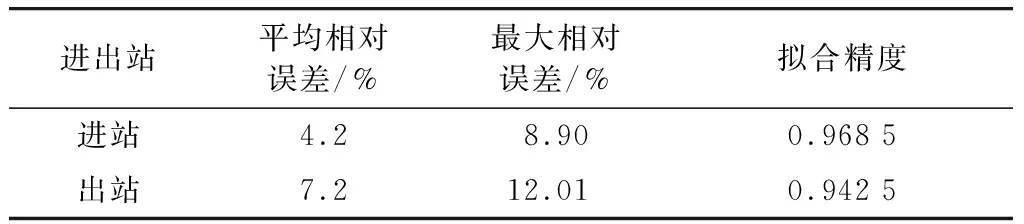
表1 预测精度指标比较
3.2 限流预警方案的制定
该线路车辆为6节编组,每节车厢核载226 人。早高峰(7:30—9:30)列车发车频率为2 min 15 s,最大满载率βmax=120%。该站为岛式站台,有效面积约540 m2。通过软件Transcad全网分配,上下行方向的平均断面客流约为1 400人次/min。经现场实际调查,以平均步行速度计算,进站口到站台与站台到出站口的步行时间均约为5 min,故m=n=1。该站为非换乘站,故Qin,tr(i)=Qout,tr(i)=Cfr(i)=Cto(i)=0人次,此外,R=1 080人次,P(i)=3 150人次。
通过限流模型计算,得出该站点限流时间为8:20—9:30;上午8:50站外排队最长,长达493人次。
图2与图3分别将是否采取限流措施的进站流率和滞留人数进行了对比。如图2所示,若未实施限流,8:20进站候车客流达到峰值,最大流率为138人次/min。而采取限流后的流率,约73~94人次/min。通过 “削峰填谷”来控制进站流率。
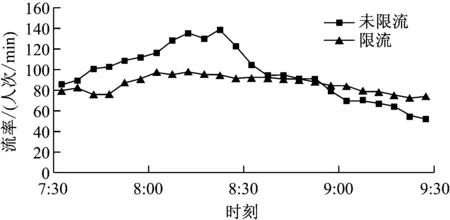
图2 是否采取限流措施的进站流率对比
如图3所示,采取限流措施情况下的实际滞留和预测滞留人数曲线非常接近,8:20是实施限流的时间分界点,该时刻之前该曲线为站台滞留人数,该时刻之后为站外排队的滞留人数,呈先上升后下降的趋势。波峰即8:50站外排队人数最多;此外,未采取限流措施的情况下,最大滞留人数为1 673人次,经计算站台最大客流密度约2.88人/m2,站台非常拥挤,存在较大安全隐患。因此,建议该站点实施限流。
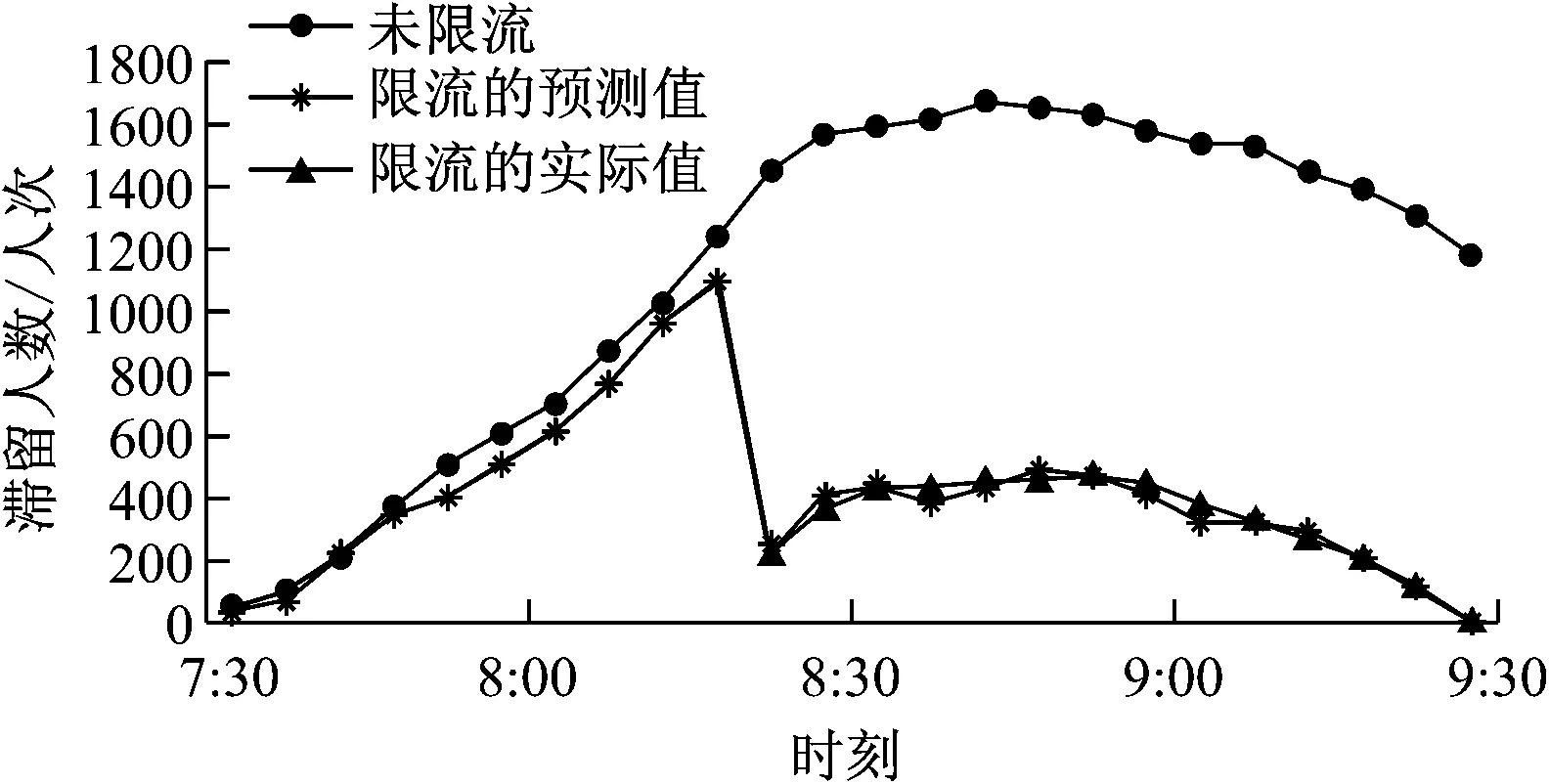
图3 是否采取限流措施的滞留人数对比
4 结语
本文研究了车站限流预警的方法,构建了站点动态限流预警模型,并选取北京地铁十号线的某站点为算例进行预警方案的计算演示,将是否实施动态限流的模型参数进行了对比,体现了实施限流对站台滞留人数的控制效果。
今后需进一步研究的方向有:① 本研究未将上下行方向客流进行区分,适用于方向不均衡系数低的站点,对于方向不均衡系数较高站点是需要研究的另一个重要方向。② 本文模型有多个参数,可直接获取或通过计算间接得出。但对于断面客流这一关乎全网客流的中间参数,为简化计算算例采用了同一估值,如何准确获取该参数的实时数据值得研究。③ 随着轨道交通网络化的发展,各个车站的客流量不断增大,单个站点限流的局限性会日益显现,多个站点的协同限流预警也是今后需要研究的一个重要方向。
