城市轨道交通自动售检票系统实时进站客流量异常检测*

张 见 张 宁 邵家玉

(1. 东南大学自动化学院，210096，南京；2. 东南大学智能运输系统研究中心轨道交通研究所，210018，南京//第一作者，硕士研究生)

城市轨道交通系统中的实时客流数据信息对提高地铁系统服务能力至关重要。然而，由于城市轨道交通自动售检票(Automatic Fare Collection，AFC)系统中的设备供应商的多样性以及实时数据传输过程的复杂性等原因，使得从AFC系统中获取的实时客流数据并不能完全反映运营实际情况，部分车站在某些时段的实时进站客流量与实际进站客流量差异较大[1]。为了保证所获取的实时客流数据的质量，可通过对各车站、各时段客流量设定合理的阈值，从而对实时获取的客流数据进行异常检测和纠错处理。在此过程中，阈值上限和阈值下限的合理设定最为关键。

根据同车站、同时段客流分布符合正态分布的特点，利用均值-三倍标准差法确定客流阈值上、下限是一种简便易行的方法，但由于样本数据本身存在异常值以及部分车站的季节性客流波动较大等原因，导致得出的阈值范围过大，不能有效地对实时获取的进站客流数据进行异常检测。文献[1]通过人工设定各样本序列均值所对应的最大阈值，得到样本序列的最大标准差，利用样本标准差与样本均值的比值判断阈值设定是否过大；文献[2]通过模型确定待检测点的预测值和方差值，以确定数据异常检测的阈值范围，取得了较好的异常检测效果。文献[3]的研究表明，混沌支持向量机回归模型对非线性时间序列回归预测效果较好。在客流预测模型建立过程中，考虑进站客流时间序列的混沌特性，以加强模型对非线性时间序列变化规律的表征能力。基于此，本文采用混沌支持向量机回归模型预测各时段的进站客流量，结合假设检验方法，利用同类日期、同时段下训练集的拟合残差构造服从特定分布的随机变量，依次计算各时段对应的进站客流预测残差在相应置信度下的置信区间，进而得到实际进站客流量的检测阈值上、下限，以期获得更有效的异常检测范围。

1 混沌支持向量机回归预测模型

混沌是指在确定性系统中出现的一种貌似无规则的、类似随机的现象[4]。文献[5]中的嵌入定理表明，通过对混沌时间序列进行相空间重构，可以还原混沌系统的非线性动力特性，从而把握混沌时间序列的性质与规律。通过计算时间序列的Lyapunov指数[6]，可以验证序列的混沌特性，而混沌时间序列在短期内是可以预测的[7]。

1.1 序列混沌特性判定

首先对时间序列相空间重构，计算时间序列的时间延迟和最佳嵌入维数，进而得出Lyapunov指数，为正则意味着该时间序列混沌。

由于C_C方法[8]具有易操作、计算量小、抗噪能力强等优点，故本文采用C_C方法计算序列的时间延迟和最佳嵌入维数。对于Lyapunov指数的计算，本文选用改进的小数据量法[4,9]进行计算，其计算步骤如下：

步骤1 采用C_C方法计算出时间序列(长度为N)的时间延迟τ和嵌入维数m，相空间重构为：

X={Xp}

(1)

其中：Xp={x(p+(m-1)τ),…,x(p+τ),x(p)},p∈{1,2,…,M},M=N-(m-1)τ。

(2)

步骤3 对相空间中的每个点Xp，计算出该邻点对的第p个离散时间步后的距离为：

(3)

步骤4 对每个q，求出所有p的lndp(q)平均值y(q)，即：

(4)

其中：q是非零dp(q)数目，用最小二乘法做出回归直线，该直线的斜率即为最大Lyapunov指数1。

1.2 实时进站客流量预测模型构建

应用C_C方法求得混沌时间序列x={xp|p=1,2,…,N}的时间延迟τ和嵌入维数m，并对原时间序列数据进行相空间重构；利用重构后的矢量数据进行单步预测，样本空间映射函数f:Rm→R，使得x(n+1)=f(X(n))，即用于模型训练与测试的样本集可表示为：

D={(X(n),x(n+1))|n=

(m-1)τ+1,(m-1)τ+2,…,N-1}

(5)

为了提高模型的预测能力和计算速度，需在模型训练之前对样本集数据的输入部分的各列数据进行标准正态分布转换，并将转换后的样本集代入支持向量机回归模型[10]中进行模型训练，同时采用大范围网格搜索寻优确定支持向量机回归模型中的惩罚系数C、不敏感系数ε以及指数径向基核函数参数λ，以优化模型的预测效果。将待预测时段的输入矢量数据进行与训练样本集同分布的正态分布转换后，代入到训练好的模型中，即可得到待预测时段的进站客流量预测值。

2 实时进站客流量阈值确定方法

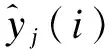
(6)

式中：

μ——该时段预测残差总体平均值；

σ——该时段残差总体标准差。

(7)

(8)

[y^(i)+e-(i)-Zα/2·s(i),

y^(i)+e-(i)+Zα/2·s(i)]

(9)

y^(i)+e-(i)-n+1n·tα/2(n-1)·s(i),

y^(i)+e-(i)+n+1n·tα/2(n-1)·s(i)

(10)

由于实时进站客流量数值为整数，故需要对置信区间的下界向上取整，上界向下取整，取整后的置信区间左端点即为阈值下限，右端点即为阈值上限。

3 实时进站客流量异常检测与处理方法

由上文可得，基于混沌支持向量机回归模型的实时进站客流量异常检测与处理的方法步骤大致如下：

步骤1 根据C_C方法确定混沌时间序列的时间延迟τ和嵌入维数m，对混沌时间序列进行相空间重构，并对相空间中的每一维的数据进行标准正态分布转换，生成训练和测试样本集。

步骤2 将转换后的样本集代入到支持向量机回归模型中进行训练，并利用大范围网格搜索对模型中的惩罚系数C、不敏感系数ε以及指数径向基核函数参数λ进行寻优，得到优化后的预测模型。

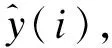
本文方法的流程描述如图1所示。

图1 进站客流量异常检测与处理流程图

4 实例分析

4.1 混沌特性分析及模型参数选定

本文数据源于南京地铁轨道交通2号线大行宫站2013年7月30日至2014年1月20日5：30—23：30之间的进站客流数据，进站客流数据的时间粒度取15 min(即第1天的5：30—5：45记为时段1，5：45—6：00记为时段2，…，23：15—23：30记为时段72，第2天的5：30—5：45记为时段73，以此类推)，该时间段内的进站客流数据的数学表示为x={x(i)|i=1,2,…,12 600}。选取长度N=3 000的子时间序列x={x(i)|i=1,2,…,3 000}，应用C_C方法计算时间序列的时间延迟τ和最优嵌入维数m，算得τ=3，m=15，利用小数据量法的改进方法求得该序列的最大Lyapunov指数λ1=0.06>0，故该地铁车站进站客流量时间序列具有混沌特性。

对原混沌时间序列进行相空间重构，并以2013年7月30日至2013年9月24日的数据作为训练数据，2013年9月25日至2013年12月28日数据作为验证数据，2013年12月29日至2014年1月20日的数据作为测试数据，对训练、验证和测试数据集进行标准化转换后，运用大范围网格搜索法优化支持向量机回归模型中的参数，即惩罚系数C、不敏感系数ε以及核函数参数λ，寻优得到优化后的模型参数C=360，ε=3，λ=0.03。

4.2 异常检测阈值确定

图2为2013年8月5—18日大行宫站进站客流数据分布图。由图可知，工作日的客流变化规律大致相同，非工作日的客流变化规律亦大致相同，但工作日与非工作日的客流分布情况差异较大。由计算可知，训练样本集中工作日与非工作日各时段残差序列的统计参量值差别较大，故各时段的模型训练残差数据要区分工作日与非工作日，利用支持向量机回归模型得到模型训练样本中各时段进站量残差数据，进而获取工作日与非工作日各时段模型预测残差的统计参量值，即样本均值、样本方差和样本数。为了测试本模型对两类日期进站量异常检测的效果，对2013年12月29日至2014年1月20日间的进站客流量数据进行了有效性检验，并给出2013年12月31日(工作日)阈值设定和异常检测的具体计算过程(非工作日计算过程与此类似)。

图2 2013年8月5—18日大行宫站进站客流量分布图

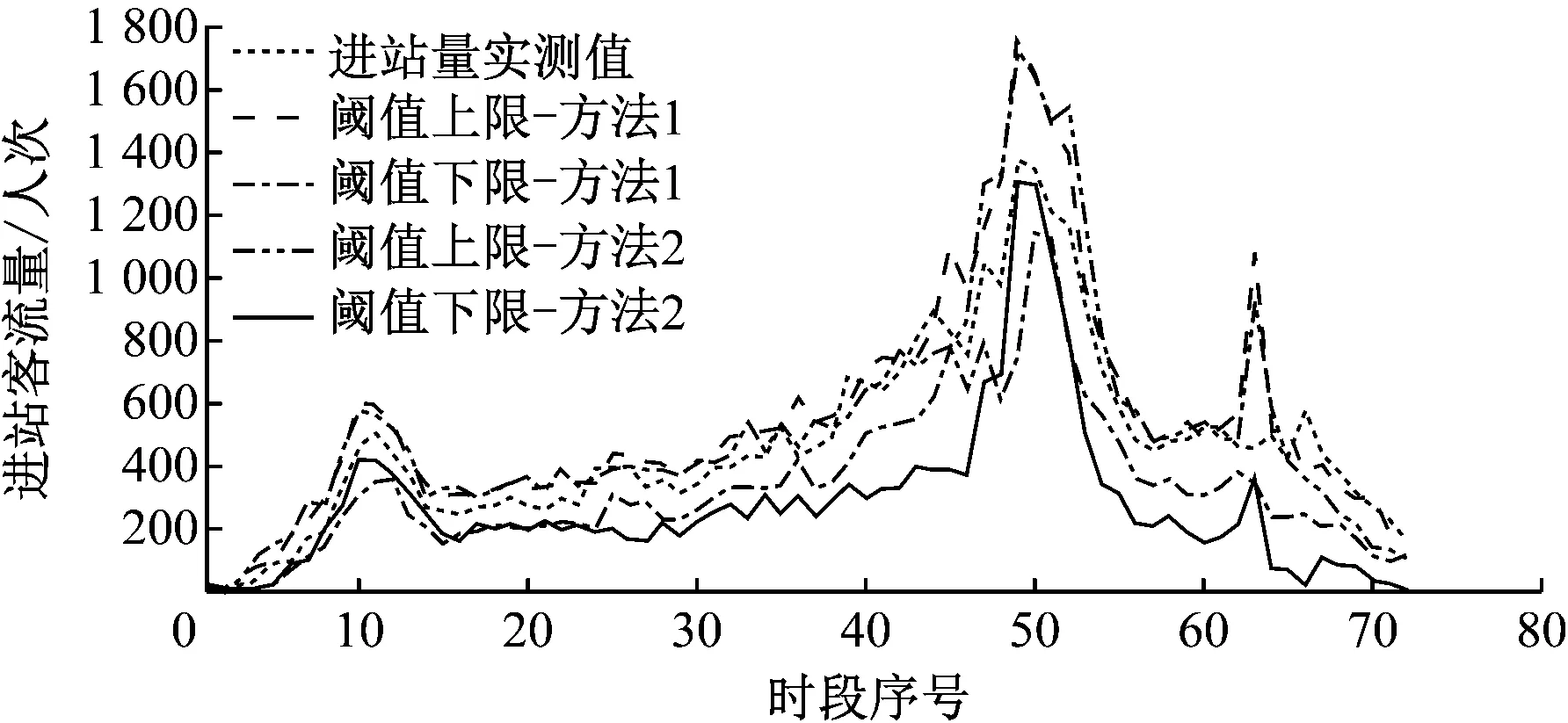
图3 2013年12月31日进站客流量异常检测阈值对比图

4.3 结果分析

应用本文阈值计算的方法(记为方法1)与文献[1]中的方法(记为方法2)得到2013年11月31日各时段的进站客流量异常检测阈值上、下限如图3所示。方法2的阈值范围主要是根据历史同期进站客流数据的样本均值和样本标准差计算确定的，并通过样本标准差和样本均值的比值对阈值范围是否过大进行判断，进而有效控制各时段阈值范围的大小；而方法1的阈值范围主要是由待检测时段的模型预测值、历史同类日期同时段进站客流数据模型预测残差序列的样本均值和样本标准差共同确定。因此，从方法机理角度分析可得，方法1相比方法2具有更好的客流规律适应能力和数据异常检测效果。通过实例计算可知，利用方法1对2013年12月29日至2014年1月20日间的进站客流量数据进行异常检测，计算得到各时段阈值范围大小的均值为223.4，数据异常检测的误报率为3.2%；而利用方法2计算得到的各时段阈值范围的大小均值为256.3，数据异常检测的误报率为5.8%。因此，方法1相较于方法2算得的各时段阈值范围收缩了12.8%，数据异常检测的误报率下降了44.8%，即本文方法有效收缩了实时进站客流量数据的有效性检测范围，降低了数据有效性检测的误报率，进一步加强了对数据有效性检测的能力。

5 结语

本文采用支持向量机回归模型进行实时进站客流量预测，根据训练集工作日和非工作日各时段拟合残差序列统计分布特性，确定实时进站客流量异常检测阈值。由实例可见，该方法有效收缩了进站客流量的异常检测范围，降低了数据异常检测的误报率，强化了对异常客流数据的检测能力，保证了实时获取客流数据的准确性和及时性，为乘客信息服务系统、实时客流预测以及大客流预警等应用提供了可靠的数据支持，从而增强了轨道交通的服务能力。