磁场中激光牵引热解石墨的理论与实验研究

李 琛，闫 江，訾昌葛，黄映洲，吴小志

(重庆大学 物理学院，重庆 401331)

热解石墨具有良好的抗磁性，能够悬浮在磁场中且其磁化率随温度线性变化. 因此，可以通过激光照射热解石墨的局部区域而导致石墨移动. 2013年日本青山学院大学首次实现用激光操纵磁悬浮石墨烯[1]. 具有负磁化率的抗磁性材料在磁场中受到排斥力，所以它们可以在磁场中被悬浮起来. 绝大部分材料仅在极低温条件下才会具有较强的抗磁性，相较于严苛的条件，一些最强的抗磁性材料，如热解石墨和铋，可以在室温下稳定悬浮在钕铁硼永磁体上，由于悬浮物与其他物体间不存在任何接触，所以可以通过很小的力进行控制，这在运输、驱动以及发展新能源等方面具有很大的研究价值.

本文中所描述的光学移动控制系统的建立仅基于钕铁硼永磁体、热解石墨片以及光源，由此所构建出的系统可以将光能直接转化为动能并且成本比较低，综合性价比很高. 通过安培分子电流假说、镜像法求解磁悬浮平台的磁场分布，通过数值模拟给出热场的分布，并且通过实验给出单个小磁体的磁场分布以及热解石墨片磁化率随温度的变化，基于此给出热解石墨片在磁场中的受力，用清晰完整的理论描述了激光牵引过程.

1 设计原理

恩绍定理[2]指出点粒子集不能被稳定维持在仅由电荷的静电相互作用构成的稳定静止的力学平衡结构. 由于恩绍定理的限制，很难使用永磁体或者简易的电磁铁实现悬浮，但可以实现抗磁性材料在磁场中的悬浮. 抗磁性材料在有外加磁场情况下的势能可以表示为[3-4]

(1)

其中,m为悬浮物的质量，g为重力加速度，μ0为真空磁导率，V为悬浮物体积，χ为磁化率，B为磁感应强度，z为悬浮高度. 稳定平衡条件为

(2)

由式(2)第二式也可以得到材料的磁化率为负，属于抗磁性材料. 由第一式可以得到材料在磁场中的受力为[5]

Fx=

(3)

Fy=

(4)

Fz=

(5)

用H替换B，将悬浮平台与抗磁性材料共同激发的磁场B替换成由悬浮平台激发的磁场与抗磁性材料激发的磁场2部分，其中激光加热引起的热分布影响抗磁性材料激发的磁场.

实验中使用的悬浮平台是由众多方形小磁铁排列而成，其排列方式如下：

1)小磁铁内部磁感应线垂直于纸面；

2)任意一块小磁铁和与其相邻的小磁铁磁极相反.

为了求解整个悬浮平台所激发的稳定磁场，首先计算单个小磁铁所激发的磁场，再将矢量场叠加，单个小磁铁激发的磁场为

dH= -

Γ(a-x,y,z)+Γ(x,a-y,z)+

Γ(a-y,x,z)+Γ(y,a-x,z)+

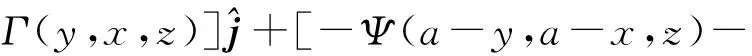
Ψ(y,a-x,z)-Ψ(a-x,a-y,z)-

Ψ(x,a-y,z)-Ψ(a-y,x,z)-

Ψ(y,x,z)-Ψ(a-x,y,z)-

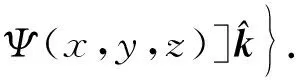
(6)

其中辅助函数为

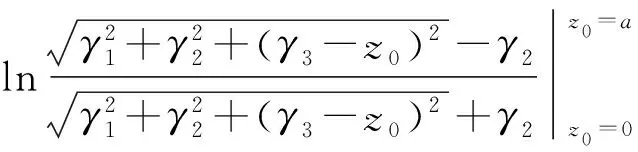
(7)

(8)

此结果与等效电流法给出的结果是相同的.

关于叠加矢量场：

H=H(x,y,z)=∑dH.

(9)

对于热场，列出热传导方程：

(10)

其中，ρ为热解石墨片的密度，cp为等压热容，λ为导热系数，P为单位体积的加热效率.

考虑到热辐射：

(11)

其中，σ为黑体辐射系数，ε为辐射率. 温度T分布在xoy平面上的数值解为

T=T(x,y).

(12)

解得温度分布如图1所示.

图1 温度分布

结合磁化率随温度变化方程

χ=βT+C,

(13)

其中β和C均为常量，可描述抗磁性材料激发的磁场：

M=χH=[βT(x,y)+C]H.

(14)

2 实验方法

2.1 磁化率的测量

实验采用液体浸泡，以达到控制实验温度的目的，则式(13)应改为[6]

(15)

其中ρ0为水的密度，B可从COMSOL的“体平均”得到.

选用圆柱形强永磁体，将悬浮物(即圆形热解石墨片)悬浮在势阱中. 选用不同厚度(不同质量)的热解石墨片，令其悬浮位置尽可能地贴近永磁体的表面(永磁体内部是均匀磁场，越贴近永磁体磁场越均匀)，逐次改变水的温度并且利用非接触式红外测温仪测量其温度，将热解石墨片的悬浮位置记录并且用软件读出其悬浮高度，如图2所示.

图2 验证磁化率随温度线性关系的装置示意图

2.2 磁场的测量

将小磁铁固定于坐标纸的合理位置，如使小磁铁内部磁感应线垂直于纸面，可以测量xoy平面内的磁场分布；如使小磁铁内部磁感应线平行于纸面，则可以测量zox或zoy平面内的磁场分布；在小磁铁下垫起不同高度的方状物质(磁化率几乎为零)，则可以实现对整个三维空间磁场强度测量. 将磁感应强度测量仪的探头对准x,y,z的某一方向，沿着坐标纸上某一直线滑动探头，同时记录位置与强度测量仪的显示数据.

2.3 临界牵引实验

a.搭建磁悬浮平台

选用边长为3 mm的立方体磁铁，水平放置指南针，将小磁铁从南北方向水平靠近指南针，若小磁铁指向东西方向，则可确定小磁体南北极，若指南针上下翻转或者转向，则转动小磁铁. 确定小磁铁的N极和S极后，做出标记.

将小磁铁按顺序排放，保证小磁铁内部磁感应线垂直于纸面，并且任一小磁铁与其相邻的小磁铁的内部磁化方向相反，搭建面积约10 cm×10 cm的悬浮平台.

b.准备悬浮物

本实验所选用的悬浮物是直径9 mm的热解石墨片，原装的热解石墨片型号与规格不同，只需砂纸打磨即可.

c.调整牵引

图3 激光牵引平台

将磁悬浮平台(如图3所示)放置在水平桌面上，将悬浮物悬浮在尽可能靠近平台中心(磁场更加均匀)的位置. 打开激光器调整到合理高度，调整激光前的准焦旋钮，使照射处激光半径最小，此时加热效果最佳，温度场热分布梯度最大，移动激光照射位置，即可实现牵引.

3 调试及结果分析

3.1 实验数据分析

3.1.1 磁化率测量数据分析

实验测得悬浮高度与温度的数据，使用Matlab对所测数据点进行拟合得到如图4所示的线性关系，实验结果测得：β=6.40×10-4K-1. 常温常压下，实验用热解石墨磁化率为-40.00[1]，则

χ=6.40×10-4T-40.19.

图4 悬浮高度与温度成线性关系

3.1.2 磁场测量数据分析

通过在2.2中所述的实验，将实验数据与理论曲线对比，得到如图5和图6所示.

图5 B-x实验数据与理论曲线对比图

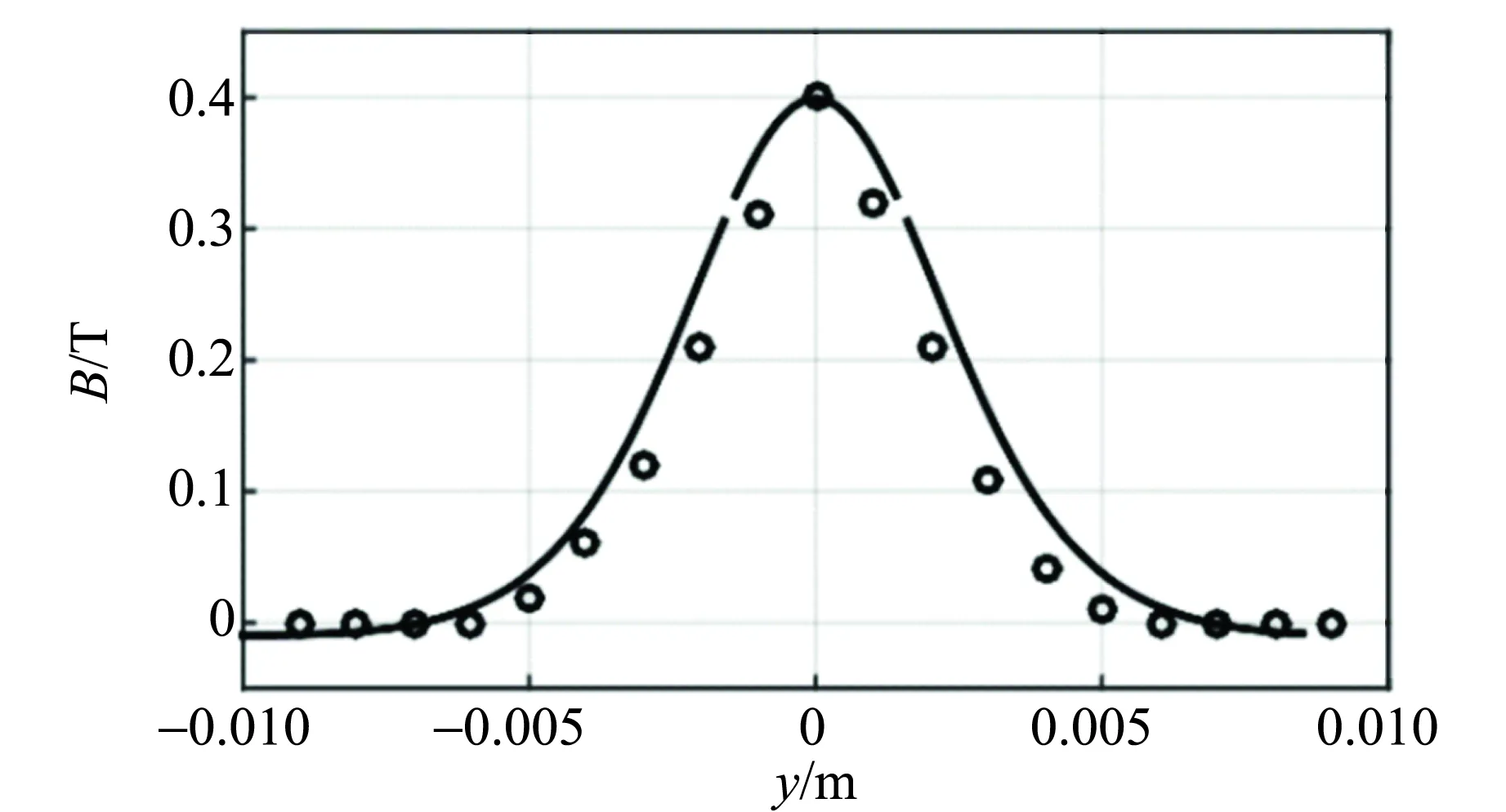
图6 B-y实验数据与理论曲线对比图

3.1.3 临界牵引分析

通过重复2.3实验，并由COMSOL模拟辅助，得临界牵引条件：激光功率为1.4 W,永磁体磁化强度为1.32×107A/m,激光器距悬浮物高度为110.0 mm,永磁体相对磁导率为1.05,悬浮物半径为6.0 mm,环境温度为297.3 K,悬浮物厚度为38 mm,悬浮物密度为2.4×103kg/m3, 热辐射率为0.87，常压热容为710 J/(kg·K),悬浮物导热系数为1 840 W/(m·K), 热解石墨相对磁导率为6.40×10-4T-39.19.

3.2 数值分析

3.2.1 热场的数值分析拟合

图7为热解石墨表面的热场分布图.

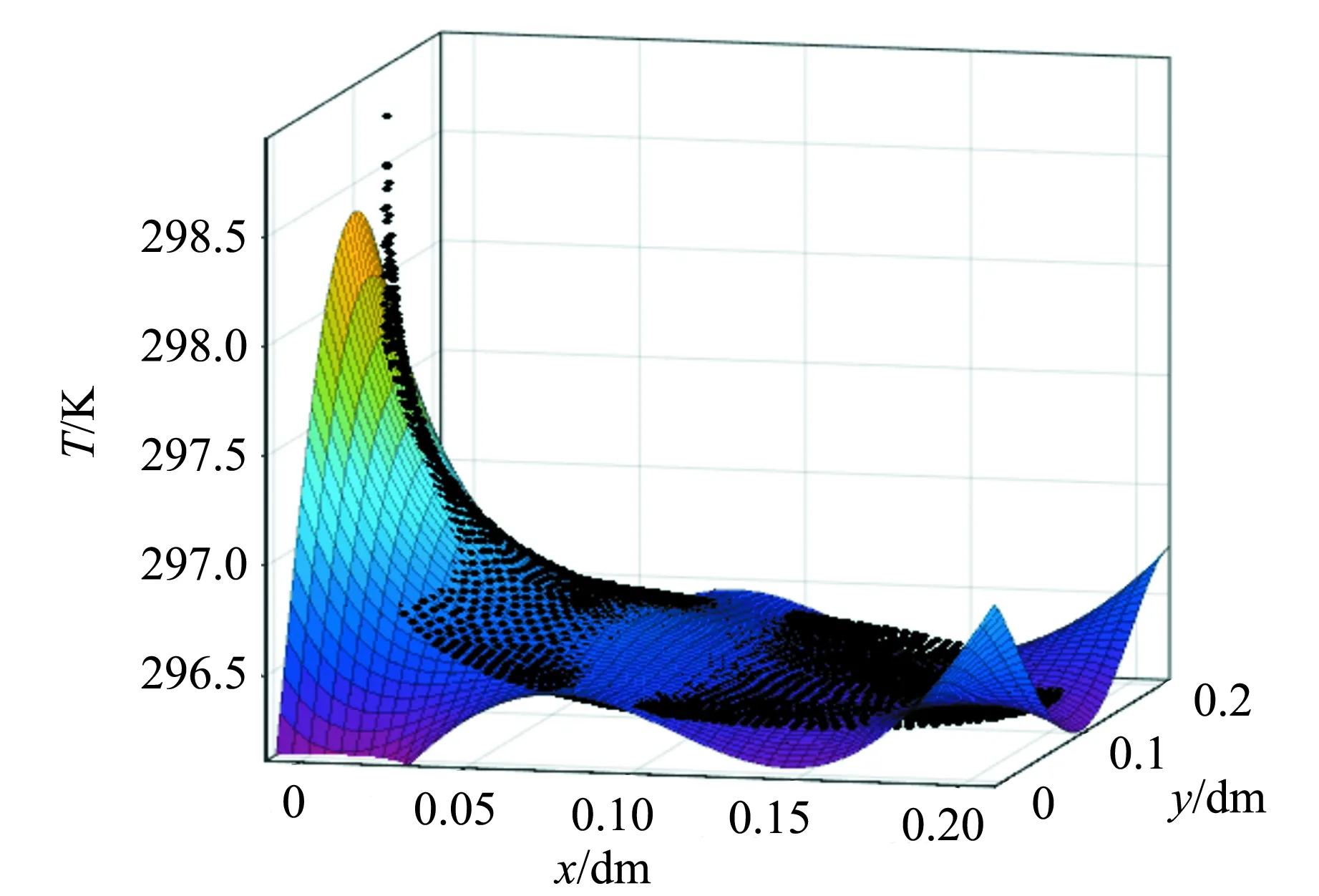
图7 热解石墨表面温度分布

3.2.2 磁化强度数值验证

商家给出的烧结钕铁硼强力磁铁的剩磁为1.32×107A/m,由前文可知求M的公式为

(16)

其中

Φx= -Γ(a-x,a-y,z)-Γ(a-x,y,z)+

Γ(x,a-y,z)+Γ(x,y,z),

Φy= -Γ(a-y,a-x,z)-Γ(a-y,x,z)+

Γ(y,a-x,z)+Γ(y,x,z),

Φz= -Ψ(a-y,a-x,z)-Ψ(y,a-x,z)-

Ψ(a-x,a-y,z)-Ψ(x,a-y,z)-

Ψ(a-y,x,z)-Ψ(y,x,z)-

Ψ(a-x,y,z)-Ψ(x,y,z),

其中辅助函数为式(7)和式(8).

最后结果如表1所示. 由表1得到

表1 任意5处数值计算得到的M值

4 数值实验

由于方程过于复杂，为了解出总体受力，需要依赖数学软件辅助运算. 为了简化研究过程，提高直观性，采用Matlab的派生软件COMSOL Multiphysics. 整个操作环境分为永磁体构成的悬浮平台、抗磁性材料构成的悬浮物以及包裹在周围的空气. 使用的2种物理场分别是“磁场，无电流(mfnc)”与“固体传热(ht)”，其间两物理场耦合采用“温度耦合(Tt)”. 研究该多物理场的稳态，其一是为了方便确认任意状态下的受力，其二是由于软件对稳态求解的优越性.

4.1 磁场，无电流(mfnc)

运行结果如图8.

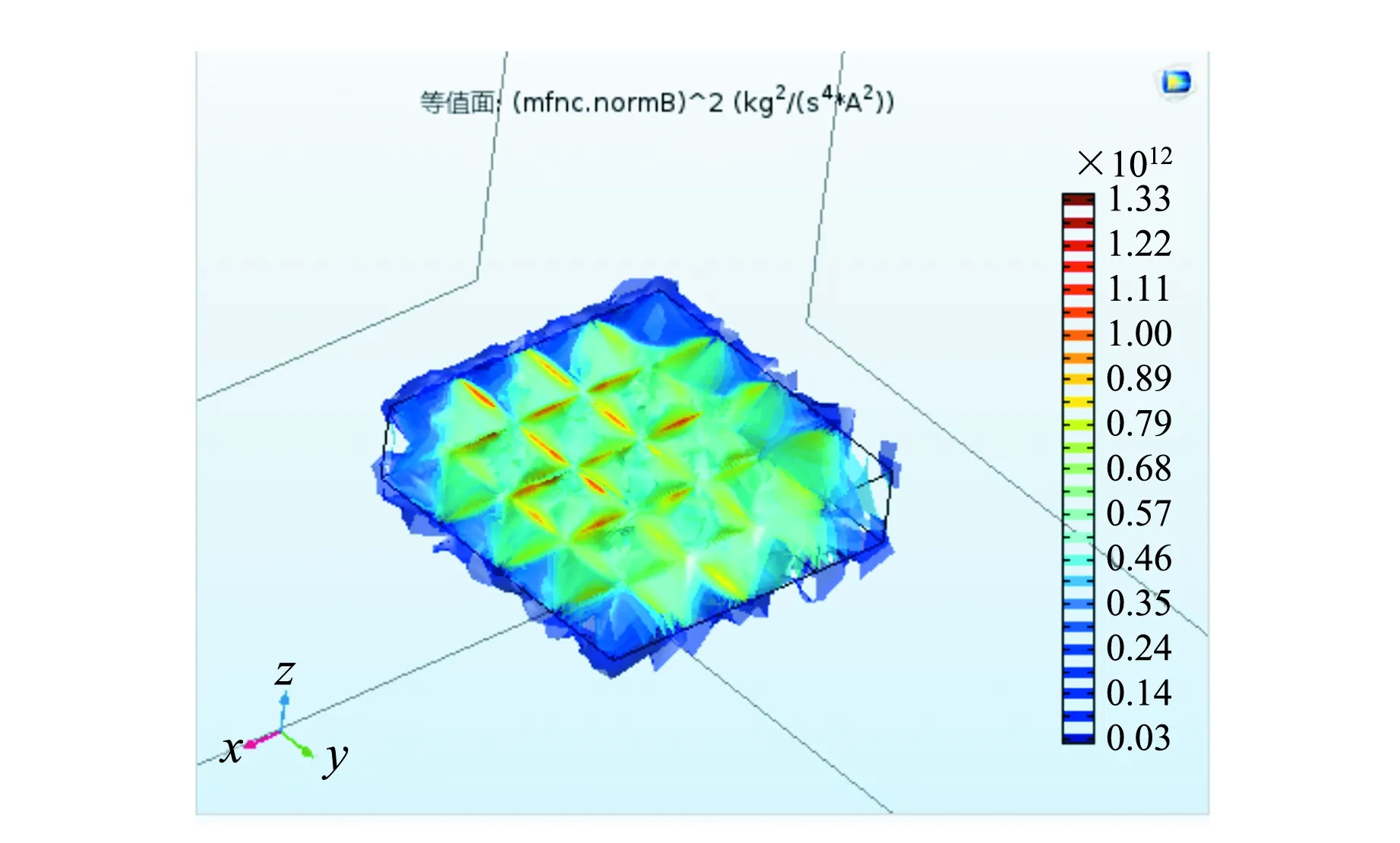
图8 磁场的COMSOL模拟

4.2 固体传热(ht)

使用漫射面实现热辐射，使用流体传热将四周空气引入热传导，使用温度来描述无限远处温度为实验室温度295 K. 在“定义”中设置“变量”引入悬浮物的相对磁导率与温度的关系.

μr=1+(βT+C).

(17)

热场运算结果如图9所示.

图9 热场的COMSOL模拟

4.3 APP的构建

为了方便运算，将COMSOL的结果结合到APP内，如图10所示.

(a)

(b)图10 APP窗口界面

该APP可实现：

a.方便改变几何、磁场、热场的参量；

b.直观显示运行结果，如磁场强度、磁感应强度、温度、相对磁导率；

c.直接得到最终受力结果.

通过该APP，用户可以便捷地求出任意坐标位置下圆形悬浮物的受力情况. 根据有限元的思想，将该结果接入Matlab窗口，可以实现对悬浮物整个牵引全过程的模拟.

5 实验现象补充说明

5.1 牵移的原因是光热而非光压

前期猜测热解石墨片被牵引的主要原因为激光的光压或光热.

光压可以通过

进行计算，其中R为材料的反射率，E为激光单位时间通过照射面积的能量，c为光速. 在实验模型中，光压在最理想的情况下量值仅10-8N，在非平稳的势能场上，这个力可能不足以克服势阱壁对热解石墨片的阻力而使之被牵移.

据此，进行了实验分析，在实验过程中将激光逆着热解石墨片预运动方向照射其预运动方向的前端，热解石墨片依然按照预运动方向移动(如图11所示)，即其实际运动方向与激光的光压水平分量相反. 因此结合理论分析和实验验证得出热解石墨片的运动不是光压，而是光热的牵引作用导致的.

图11 牵引实验

5.2 激光照射下，热解石墨片迅速达到热平衡且温差较小

激光功率直接影响牵引的效果，在使用COMSOL进行热解石墨的温度模拟时，发现功率越高的激光能够使热解石墨片达到的最大温度越高，达到最大温度所用的时间越短，两端形成的温差越大，从而使牵引更加容易.

容易看出，无论激光功率大小，其使热解石墨片两端达到恒定温差的时间都十分短暂，而且都在照射后1 s左右达到稳定. 在实验室中使用100 mW和1 W的激光对热解石墨片进行牵引，发现前者无法牵动热解石墨片，而后者效果十分显著.

使用非接触式激光测温计(测温计识别光波频率与牵引所用激光频率相差甚远，不会被其干扰)测量激光加热时的热解石墨片温度分布，发现加热点与边缘的温差在1 ℃左右.

5.3 热解石墨片的旋转实验及简要分析

除了牵引实验外，使用同心N和S极交替排布的圆柱磁铁悬浮热解石墨片，如图12所示.

图12 激光照射旋转实验装置示意图

激光照射热解石墨片中央，热解石墨片无明显现象；激光照射边缘时，热解石墨片发生了旋转；激光再次照射热解石墨片中间，热解石墨片停止旋转；激光照射热解石墨片另一边，热解石墨片再次旋转而且旋转方向与前相反. 激光照射旋转实验现象示意图如图13所示，箭头表示旋转方向，紫色点表示激光照射位置.

对此现象分析：悬浮后的热解石墨盘在光照射后立即向照射部位移动，此时，热解石墨片受到来自磁势壁的排斥力，理想情况下，排斥力与运动方向相反. 然而，由于由钕铁硼磁体产生的磁场的不均匀性，实际的排斥力可能会稍偏离重心线.

因此，产生朝向热解石墨片的切线的力而使热解石墨片发生旋转.

图13 激光照射旋转实验现象示意图

6 结束语

在光热效应下，实现了激光牵引. 用永磁体搭建悬浮平台，抗磁性物质做悬浮物. 从悬浮物受力公式出发，将其分为磁场与热场2部分影响，分别对2个场进行分析，结合Matlab给出理论公式与方案，通过实验验证了理论的自洽性. 使用COMSOL进行数值模拟，给出定位情况下的受力情况、磁场分布以及热场分布等. 建立了相关APP，使悬浮物在平台上各点的情况都可以计算得到，从而让牵引过程更加精确和直观.