电热法测热功当量实验数据处理方法
2018-11-02何建勋
何建勋,唐 芳
(北京航空航天大学 a.能源与动力工程学院;b.物理科学与核能工程学院,北京 100191)
热功当量实验是验证能量守恒和转化定律的基础实验[1],其在装置的设计、操作技能的训练和数据处理方法的研究等方面都有助于对学生能力的培养[2],因此无论在物理学的发展还是在实验教学中,热功当量的测量实验均具有较大的意义[2]. 目前实验教学中普遍采用电热法测量热功当量,我校教材中该实验的数据处理采用“差分代替微分”法求解热功当量[3],这种方法只需记录加热升温数据,但从我校实验经验上看,实验所得的线性相关系数较低、且热功当量测量误差通常较大[4].
本文基于温度补偿原理和牛顿冷却定律,对电热法测量热功当量实验提出了2种散热修正方法,即温度补偿法和线性回归法. 首先简单介绍电热法测量热功当量和2种新的散热修正方法;然后对同一批数据用不同的方法处理并比较;最后针对线性回归法,讨论测点数目和测点时间间隔对实验准确度的影响,给出实验方案选择建议.
1 电热法测量热功当量的基本原理
热功当量可定义为传热量和做功量单位之间的数量关系[1]. 电热法测量热功当量实验在量热器中进行,用电阻加热器向量热器系统加热,加热过程中电流做功为
(1)
式中,U为加热器两端的电压,R为加热器的电阻,t为加热时间. 在不考虑散热的情况下,即假设电流做功全部转化为热量,使盛水的量热器系统由初温T0升到T,系统吸收的热量为
Qab=(c0m0+c1m1+c2m2)(T-T0)=Cm(T-T0),
(2)
式中c0,c1,c2分别是水、量热器和电阻加热器的比热容;m0,m1,m2分别为其相应的质量;Cm为系统的总热容. 所以热功当量J满足:
(3)
即
如果各量均取国际单位,则热功当量理论值J=1. 然而,即使实验在量热器中进行,系统和外界不可避免地会发生热量交换,一般会根据牛顿冷却定律进行散热修正[3,5]. 当系统和环境温差较小时,牛顿冷却定律可表述为[6]:

(4)
其中δQra为系统的散热量,T和T∞分别为系统和环境的温度,k为系统的散热常量. 依据能量守恒关系,系统热力学能增量等于其从加热器的吸热量与其和外界散热量的代数和,综合式(1),(3)和(4),系统温度需满足
(5)
式(5)为按照牛顿冷却定律修正的热功当量测量公式.
2 2种散热修正方法的基本原理
2.1 温度补偿方法的原理
温度补偿法借鉴了测量冰的熔解热实验中广泛使用的补偿原理[2]. 在热源供热速率恒定且不大、系统导热性能良好、搅拌充分均匀的条件下,系统的温度变化过程可以认为是准静态过程,即在任意时刻系统都处于平衡状态[7],可以通过测量系统内一点的温度来代替系统温度.
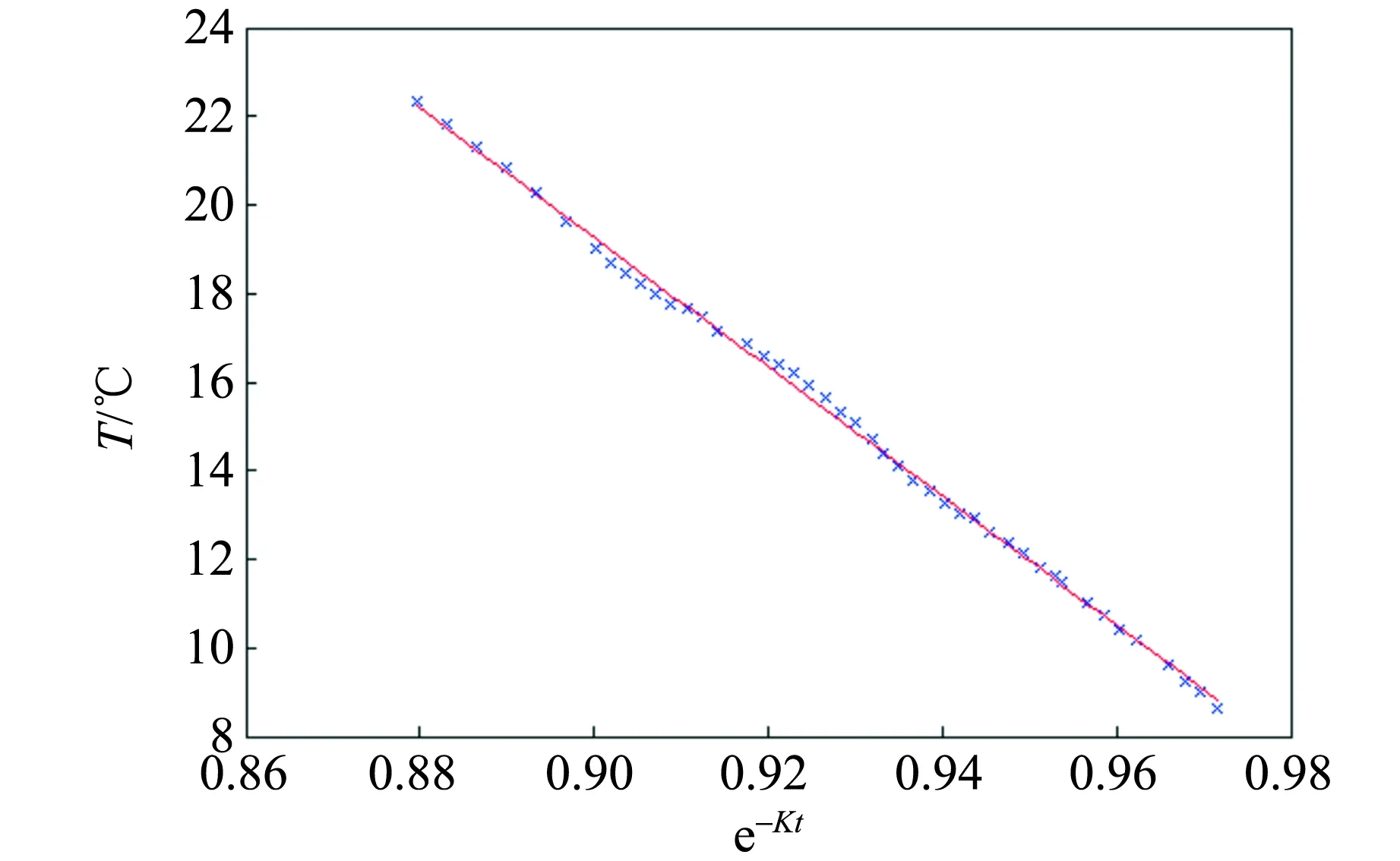
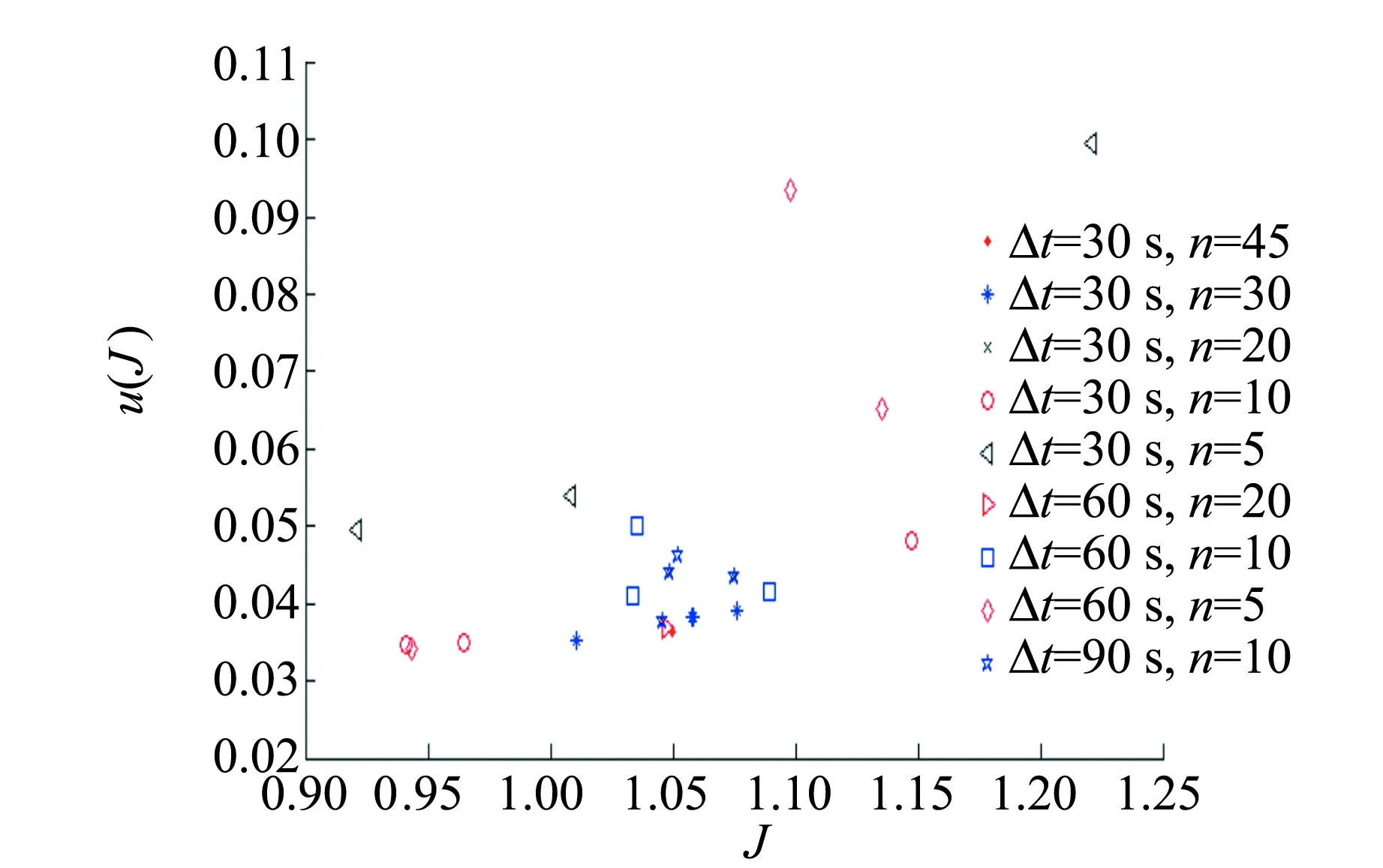
设实验中系统温度随时间变化的大致趋势如图1中黑线所示,其中0-1段为加热前的过程,由于此时各时刻系统温度低于环境温度,即T (6) 式(6)中等式左边为全过程中系统的热力学能增量,等式右边第一项为系统对环境的散热量δQra,第二项为系统从加热器吸热量δQab. 根据积分定义,等式右边第一项可用系统的T-t图像和T∞所围面积的代数和表示. 若用图1所示的面积定义,则: (7) 在T-t图像上取一时刻t1′,过t1′作垂直于t轴的直线,并延长线段0-1和2-3,使得其与T-t图像所围面积S2,S3和S5满足S2+S3=S5,则存在一假想加热过程,系统温度随时间的变化如图1中红线所示. 其中0~t1′为加热前的自然升温,电加热过程在t1′时刻瞬间完成,t1′~t3为加热后自然降温. 由于加热过程在瞬间完成,所以系统与环境间的传热不发生在电加热过程中,而仅发生在0~t1′、t1′~t3两过程中. 在假想加热过程中,系统和环境的传热可用图1所示面积表示为 (8) 图1 实验温度随时间变化的趋势和补偿原理 由于作图保证S2+S3=S5,由式(7)和(8),在图1所示的0-1-2-3过程和0-1′-2′-3过程中,系统向环境间的散热量相等,又因为系统的初末状态相同(均为0状态和3状态),依据能量守恒关系,系统向外界的吸热量等于初末状态热力学能的增量与系统向外界做功量之和[8],所以两过程中系统从加热器的吸热量Qab相等,可以用0-1′-2′-3过程代替实际过程进行研究. 而且,因为在0-1-2-3和0-1′-2′-3过程中,仅有1-2段和1′-2′段存在从加热器吸热的过程,所以1-2段和1′-2′段的加热量相等. 又因为1′-2′段的加热过程无时间积累,不存在对环境的散热,所以无论是0-1-2-3还是0-1′-2′-3过程,加热量Qab均等于1′状态和2′状态热力学能的差,即 (9) 在实验数据处理时,延长2个散热过程的温度曲线,并在t轴上取t1′时刻,使得T-t图像上的面积满足S2+S3=S5,得到修正后的初末温度T1′和T2′,代入式(9)即可计算热功当量. 上述温度补偿方法可以修正实验中的散热,其原理清晰且计算量小,可行性强;但必须测量自然升温和自然降温过程,所以尝试基于牛顿冷却定律的二重线性回归法. 由实验条件可得,本实验中系统和环境的换热可近似看作大空间内的自然对流换热. 由传热学实验关系式[6],大空间自然对流换热的散热常数k与系统和环境间的温度差ΔT有关,为 k=Cn(ΔT)n 其中n为由实验确定的指数,操作中根据特征格拉晓夫数Gr的范围而取不同的值,可取区间为(0.25,0.33),Cn为指前系数. 对本实验对应的对流换热条件,n取值应为0.33[6]. (10) 求解式(10)微分方程,可得加热过程中温度的变化为 (11) 同理可解得自然对流过程中温度的变化 T=C2e-Kt+T∞, (12) 式(11)和(12)中的C1和C2均为积分常量,由初始条件确定. 对式(11)和(12)进行线性化变换,将式(12)移项并取对数得 ln (T-T∞)=-Kt+lnC2. (13) 令Y=ln (T-T∞),X=t,则式(13)满足Y=-KX+c的形式. 所以在自然对流过程中对ln (T-T∞)和t做线性拟合,由拟合系数可求得K. 在加热过程中令Y=T,X=e-Kt,则式(11)同样满足Y=aX+b的形式. 所以,在加热过程中对T和e-Kt做线性拟合,由拟合结果可以计算热功当量: (14) 而且,由于假设全过程中系统与环境的散热常量保持不变,所以第二次拟合中的K值可用第一次拟合的结果代替,即第二次线性拟合和计算时的K值已知. 以下分别用温度补偿法和二重线性回归法,对同一组实验数据进行处理,并对处理结果进行比较. 取某次实验测量结果,作出加热前自然升温过程、加热过程和加热后自然降温过程中的T-t图像,并对自然升温和自然降温过程做线性拟合,对加热过程做多项式拟合. 可以得到,拟合相关系数均在0.99以上. 根据2.1节的温度补偿原理,做出类似图1的假想过程,用红线表示,即延长自然升温和自然降温过程,并使加热升温瞬间完成,如图2所示. 图2 某次实验数据及其温度补偿结果 由温度补偿法可得出已修正的加热初温T1′和末温T2′,代入式(9)即可求热功当量. 修正后的加热初末温度分别是:T1′=8.81 ℃,T2′=22.34 ℃,求得热功当量结果为J=1.03. 为方便比较,现选用与3.1节相同的测量数据,用二重线性回归法进行处理. 全过程升温范围约13 ℃,散热常数k在全过程中可看作常数. 根据自然降温过程的T-t测量结果,对ln (T-T∞)和t做线性拟合,拟合结果如图3所示. 图3 自然降温过程中ln (T-T∞)和t的线性拟合结果 拟合相关系数为r=-0.997 1,线性关系良好,由拟合斜率可以求得K=6.413 7×10-5. 假设全过程中K保持不变,在加热过程中对T和e-Kt做线性拟合如图4所示. 图4 加热升温过程中T和e-Kt线性拟合结果 拟合相关系数r=-0.999 2,线性关系良好,理论推导与实际测量结果无明显偏差,由拟合截距结合式(14)可计算热功当量,计算结果为 J=1.049 7. 现考虑由此方法求得热功当量的不确定度估计,测量结果的不确定度主要有仪器误差造成的B类不确定度和由拟合误差造成的A类不确定度. 相较于拟合误差,温度、时间、质量等测量的仪器误差很小可忽略不计. 所以这里在进行不确定度合成,仅对拟合误差造成的A类不确定度进行合成. 由第一次拟合关系式(12),结合回归系数不确定度的计算方法可求得 (15) 同理由第二次拟合关系式(11)可求得 (16) 由式(15)和(16)结合式(14)以及不确定度的合成原则可求得 按照上述方法,本节算例中的不确定度u(J)计算结果为u(J)=0.036 2≈0.04,所以本算例热功当量的最终表达为J=1.05±0.04. 2种方法均可对散热进行修正,得出较准确的热功当量结果,在原理和具体实践中都是可行的. 相较而言,温度补偿方法借助图形工具,将系统与环境的散热量转化为T-t图像中的面积,省却了复杂的散热微分方程的求解,使数据处理更加直观简便. 二重线性回归法可通过求解散热常量恒定假设下的散热微分方程,得出完整而严格的数据处理原理. 然而该方法处理过程相对较复杂计算量大. 并且实际过程中的散热常量并非恒定,而是和系统与环境的温度差有关[6],由此引入的近似也会带来实验误差. 二重线性回归方法可以得到完整严格的数据处理原理,但计算量过大的问题仍需解决. 理论上,在不影响结果准确度的前提下适当减少测量点的数目可以减少数据处理的工作量. 一般而言,在总时间不变的前提下增大相邻测点的时间间隔Δt,或在时间间隔不变的情况下减少测点的数目n均可减少测量点的数目. 为讨论这2种方法对准确度的影响,在相同条件下改变测点数目进行了多次实验,图5为加热升温阶段测点间隔及测点数目同计算结果的关系对比. 图5 加热升温测点间隔和测点数目对计算结果影响 总体而言,测点数目和相邻测点的时间间隔对实验结果存在影响. 加长实验时间并密集测点有助于降低实验结果的误差,提高实验结果的准确度. 然而过长的实验时间将会增加实验过程中环境因素的不确定性,不利于结果的准确. 由图5可得,当Δt取为30 s时,在n≥20的情况下实验结果的分布较密集,数据的重复性好;在n=10或5时,实验结果分布则较分散,数据的稳定性欠佳,且出现了较大不确定度的情况,说明拟合相关性不好. 当Δt由30 s增加到60 s而n不变时,计算结果的重复性和准确度即可得到改善,说明在测点数量不变时,适当增加实验的总时间,即增加相邻测点的时间间隔可降低实验结果的不确定性,使结果更稳定. 当Δt=60 s时,若n减小至5则同样会出现结果分散,此时实验结果的可信度低. 所以为了保证实验结果的准确性,测点间的时间间隔不宜过小,一般不能小于60 s;测点数量不宜过少,一般不能小于10;当时间间隔加长至90 s时,测点数量也需为10. Δt和n的最佳取值分别为Δt=60,n=10. 基于牛顿冷却定律,提出了2种对热功当量实验的数据处理方法,即温度补偿法和二重线性回归法,二者均可降低散热带来的系统误差,得到较准确的实验结果. 温度补偿法不涉及复杂的数学推导,数据处理更加直观和简便;线性回归方法来源于对散热微分方程的求解,在数学上更加严格,且能给出实验结果的不确定度估计. 为解决线性回归方法数据处理工作量大的问题,可在保证实验准确度的前提下适当减少实验测点的数目,合适的Δt和n取值为:Δt=60,n=10. 使用此方法进行数据处理,可以明显解决“差分代替微分求解散热量”方法中线性相关系数低、误差较大的问题,得到准确的结果.



2.2 二重线性回归方法的原理
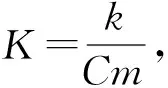
3 结果与讨论
3.1 温度补偿法的处理结果

3.2 二重线性回归法的处理结果

3.3 2种方法的比较
4 关于二重线性回归方法的进一步讨论
5 结束语
