高孔洞率复合保温砌块设计及热工性能影响因素

苏宇峰， 梁世英

(1.同济大学 材料科学与工程学院， 上海 201804； 2.同济大学 先进土木工程材料教育部重点实验室， 上海 201804)

复合保温砌块包括混凝土空心复合保温砌块和烧结复合保温砌块等，由实体材料及孔洞中填充的保温材料构成，在中国已经得到生产和应用.许国东等[1]分析了孔型、含水率和复合无机保温板对混凝土复合保温砌块热工性能的影响；Zach等[2]将真空绝热板填充于陶粒混凝土空心砌块的空腔中，以提高陶粒混凝土砌块的保温隔热性能；于献青等[3]总结了烧结复合保温砌块的研制过程，对比了夹芯和填芯2种复合方式对该砌块热工性能的影响；孙孟琪等[4]采用ANSYS软件研究了烧结保温砌块的孔洞数量、形状以及肋的数量对墙体传热性能的影响；浮广明等[5]通过ANSYS软件研究了孔的长宽比等不同因素对烧结保温多孔砌块热工性能的影响.ABAQUS有限元软件也经常应用于墙体传热分析.张国永等[6]采用ABAQUS软件对烧结复合保温砌块的热工性能进行数值模拟，研究了传热路径对其保温性能的影响.

为适应国内建筑节能新发展，需设计和研发高效复合保温砌块，以大幅提升自保温砌块外墙的热工性能.本文针对高孔洞率复合保温砌块，提出了孔型设计方法，并应用ABAQUS有限元软件研究了孔型排布、孔洞率和组成材料导热系数对其热工性能的影响.

1 试验

1.1 原材料

复合保温砌块中实体材料和填充的保温材料对其热工性能均有影响.参照不同干密度级别的混凝土、烧结砖或烧结砌块，以及膨胀珍珠岩、有机保温板、气凝胶等保温材料的导热系数，同时兼顾分析计算的系统性，本文设定了用于有限元模型计算的实体材料和保温材料的导热系数λS，λW，见表1.

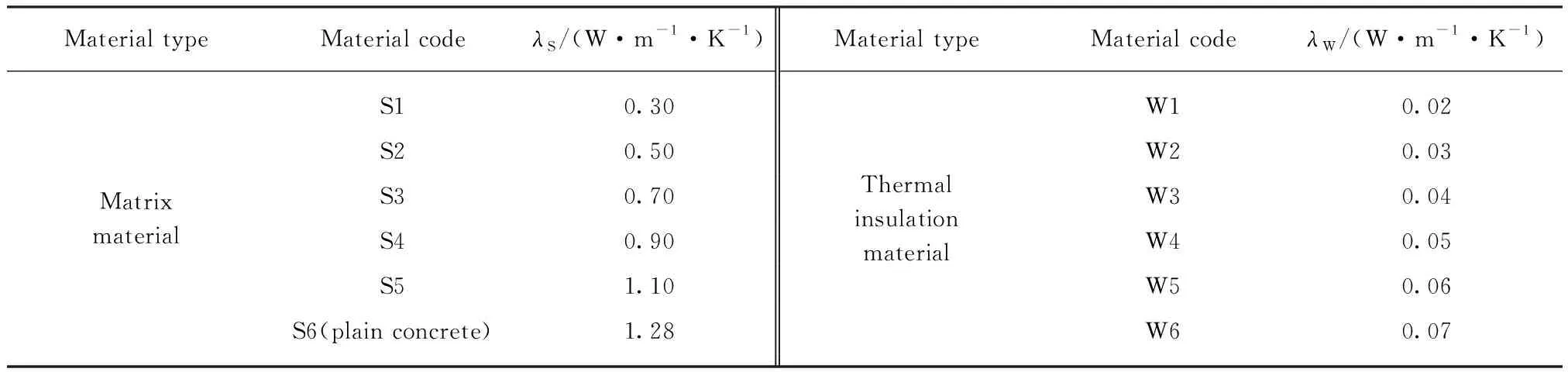
表1 实体材料和保温材料的导热系数

1.2 试验模型设计

参照混凝土基和烧结材料基复合保温砌块的国家标准，本文设计的复合保温砌块外观尺寸为390mm×240mm×190mm；孔型分别为单排孔、双排孔、普通三排孔和交错三排孔，用模型M1，M2，M3，M4表示，见图1；各模型中，平行于砌块长度方向的横壁(横肋)厚度(h)相同，垂直于砌块长度方向的纵肋厚度(b)也相同，即每个模型中的孔洞尺寸相同且均匀分布，其中模型M4中交错分布的纵肋厚度b′=1.5b.

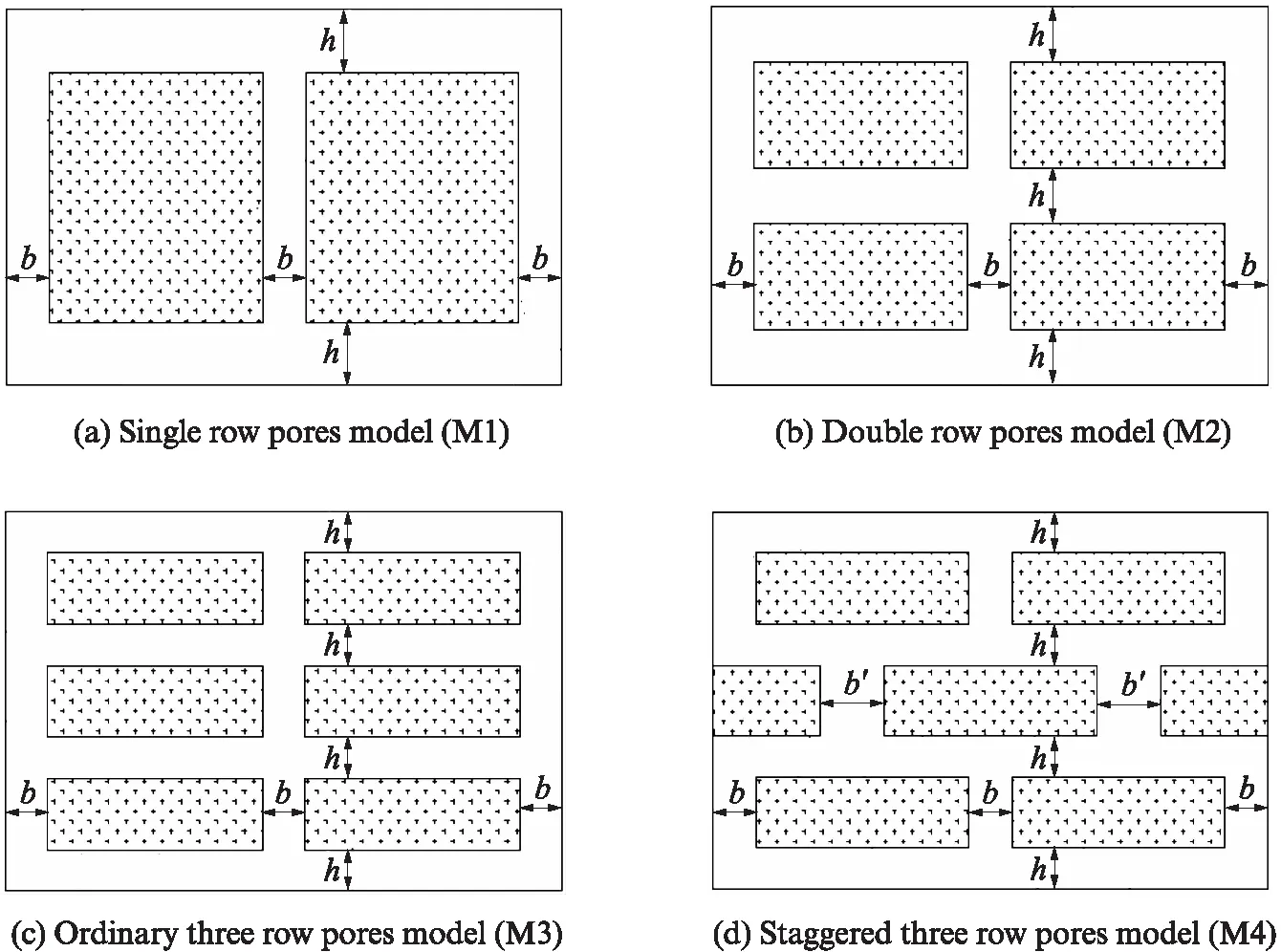
图1 模型示意图Fig.1 Model diagram

复合保温砌块的孔洞率k可按式(1)计算，转换后可得横壁(横肋)厚度h和纵肋厚度b的相互关系式，见式(2)和式(3).由此可设计出不同孔洞率下纵肋和横壁(横肋)尺寸，见表2.

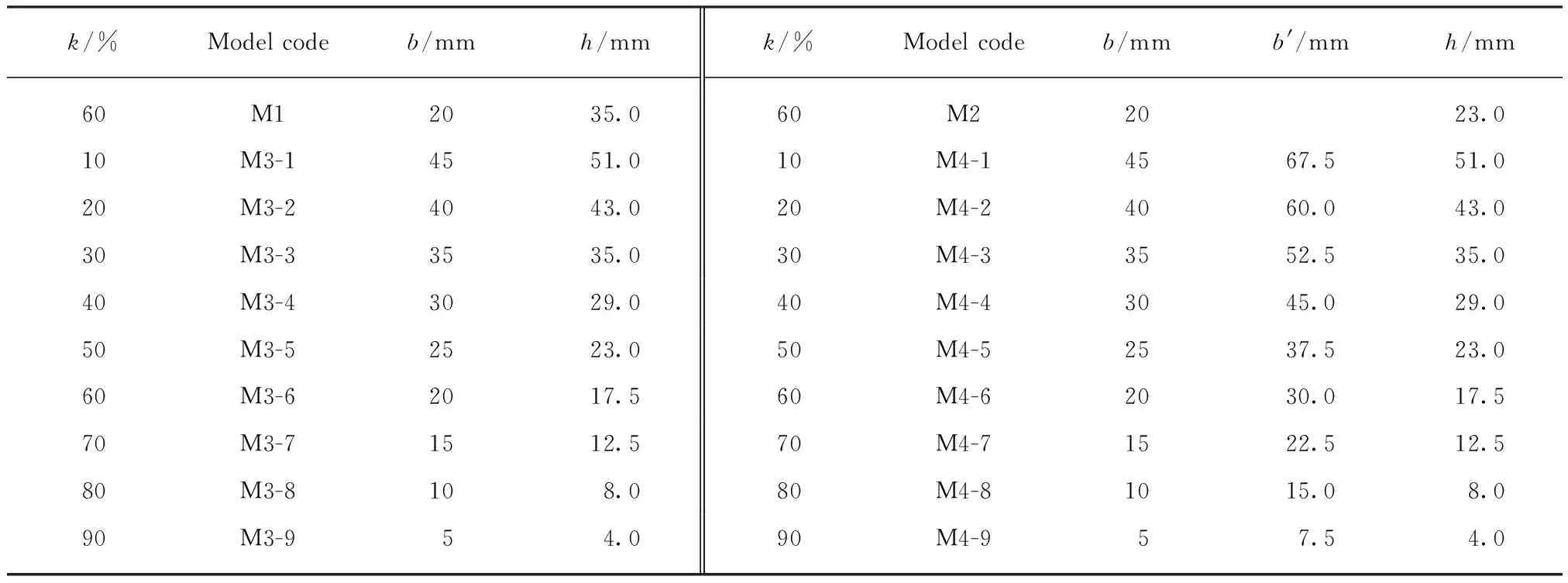
表2 模型编号和孔壁尺寸

(1)

(2)

(3)

式中：k为复合保温砌块孔洞率，%；L，H分别为复合保温砌块的长度和宽度，mm；m，n分别为纵肋和横壁(横肋)的个数.

1.3 ABAQUS传热分析过程

本文应用ABAQUS有限元软件对复合保温砌块进行稳态热分析，其计算过程[7]如下：

(1)根据1.2节中设计的复合保温砌块模型结构和尺寸创建部件.

(2)定义实体材料和保温材料的导热系数，本文未考虑材料干密度和比热容的影响.

(3)装配部件，并假设不同材料之间完全接触，即忽略不同材料之间的接触热阻[6].

(4)设置稳态热传递的分析步，并设置场输出为热通量.

(5)在复合保温砌块两侧表面施加温度荷载，分别为20℃和-10℃(模拟寒冷地区外墙内外表面的温度).复合保温砌块的其他边界均为理想绝热条件.

(6)选择适用于热传递的DC2D4四节点线性传热四边形单元，扫掠划分网格.

(7)提交作业并监控其分析状态，注意是否有警告和错误提醒.

(8)得到复合保温砌块的热流密度云图及各单元热流密度的计算结果.

由复合保温砌块中各单元的热流密度值，计算其平均热流密度q，则复合保温砌块的热阻R按式(4)计算；在灰缝厚度很小、对墙体传热影响很小时，复合保温砌块外墙的传热系数K按式(5)计算.

(4)

(5)

式中：R为复合保温砌块热阻，m2·K/W；t1，t2分别为复合保温砌块两侧的表面温度，℃；q为复合保温砌块平均热流密度，W/m2；K为砌块单一外墙的传热系数，W/(m2·K)；Ri，Re分别为单一外墙的内、外表面换热阻，m2·K/W.

2 结果分析及讨论

2.1 孔型对热工性能的影响

为分析孔型及其排布对复合保温砌块热工性能的影响，采用文献[8]中自保温砌块平均热阻的计算公式(见式(6))，计算模型M1，M2，M3-6的平均热阻；同时采用ABAQUS有限元软件计算孔洞率均为60%的模型M1，M2，M3-6和M4-6的热阻.计算时，实体材料选用S1，保温材料选用W6，计算结果见表3.

(6)

式中：F0为与热流方向垂直的总传热面积，m2；F1，F2，…，Fn分别为按平行于热流方向划分的各单元传热面积，m2；R0·1，R0·2，…，R0·n分别为各单元传热面部位的传热阻，m2·K/W；φ为修正系数.

表3 孔型及排布对模型热阻R的影响

由表3可知，模型M1，M2和M3-6根据式(6)计算得到的热阻是相同的，这是因为这3个模型不仅纵肋厚度相同，即各部分传热面积相同，而且各部位的传热阻也相同.而采用ABAQUS软件计算时，各模型热阻有微小差异，模型M3-6(普通三排孔)的热阻较模型M1(单排孔)增加了2.1%，即随着孔洞排数的增加，复合保温砌块的热阻有所增加，这与文献[1]中实测数据的趋势相符.

从表3中还可看出，采用ABAQUS有限元软件计算得到的结果略大于按文献[8]计算得到的结果，但其偏差均小于3%.参照GB 50176—2016《民用建筑热工设计规范》规定：对于由2种以上材料组成的非匀质围护结构，当相邻部分热阻的比值大于1.5时，其热阻应采用稳态传热软件计算.因此可认为采用ABAQUS等计算软件计算的热阻更有效.

模型M3-6和M4-6的孔洞率完全相同，而当模型M4-6在保持纵肋总厚度不变的情况下移动了部分纵肋位置时，其热阻较模型M3-6增加了1.6%.其原因一般被认为是热流更容易沿着实体部分传递，当砌块中纵肋交错排列时，传热路径延长了，致使砌块的热阻增加[6].

图2是采用ABAQUS软件计算得到的各模型热流密度云图.从图2中可以更清晰地分析模型各部位在传热过程中的作用.各模型中，热流密度最大值出现在模型M1中间的纵肋上(A处)；中间纵肋的热流密度随横肋个数增加而逐渐减小，但比两侧纵肋的热流密度大；纵肋的热流密度均比横壁(横肋)和保温材料中的热流密度大，即热流主要通过纵肋传递.

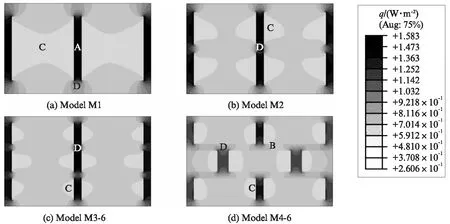
图2 热流密度云图Fig.2 Heat flux density contour

通过横壁(横肋)的热流密度比纵肋小，但比保温材料大，且影响相邻保温材料的热流.在模型M1中，其影响区域尚不足以贯通保温材料，但在模型M2和M3-6中，其影响区域已经贯通保温材料；在模型M4-6中，虽然中间的横肋是实体贯通的，但在热流密度云图中是不连贯的，即出现了某种程度的“断桥”现象(B处).

热流密度最小值出现在保温材料中，但其面积(C处)随孔洞排数的增加而逐步减小，且在模型M2，M3-6，M4-6中只出现在纵肋旁边.

纵肋和横壁(横肋)实体交接处(D处)，热流密度呈扩散态，说明横壁(横肋)分散了纵肋中集中的热流密度，热量在D处由纵肋扩散到横肋，即横肋中的热流密度较纵肋低.

通过以上分析可知，与单排孔砌块相比，双排孔和三排孔砌块由于增加了中间横肋，导致其热流密度云图发生了较大变化，部分降低了热流传递效率、增加了微量热阻；在交错三排孔模型M4-6中，由于纵肋不贯通，甚至在横肋处出现了某种程度的“断桥”，使热阻出现了较大增加.

2.2 孔洞率对热工性能的影响

为研究孔洞率对复合保温砌块热工性能的影响，采用ABAQUS软件模拟计算模型M3和M4系列的热阻.计算时，实体部分材料选用S1，保温材料选用W6，计算结果见图3.

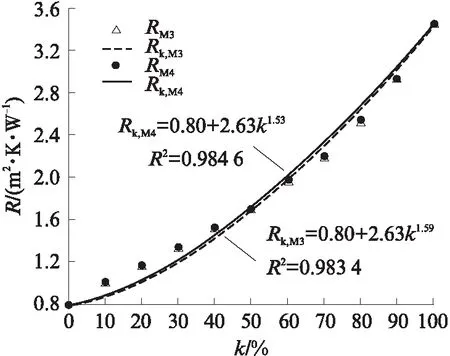
图3 孔洞率对热阻的影响Fig.3 Influence of porosity on thermal resistance

从图3可以看出，随着孔洞率的增加，普通三排孔和交错三排孔模型的热阻均逐渐增加.当孔洞率由10%增加到90%时，普通三排孔砌块的热阻从0.99m2·K/W增加到2.92m2·K/W，增加了195%；交错三排孔砌块的热阻从1.00m2·K/W增加到2.93m2·K/W，增加了193%.

采用MATLAB软件对试验数据进行拟合，得到普通三排孔和交错三排孔砌块的热阻随孔洞率k变化的计算公式，见式(7)和式(8)：

Rk，M3=0.80+2.63k1.59

(7)

Rk，M4=0.80+2.63k1.53

(8)

式中：Rk,M3，Rk,M4分别为模型M3系列和M4系列的热阻，m2·K/W.

采用上述类型公式，主要是兼顾孔洞率为0%和100%的极端情况.无论是普通三排孔还是交错三排孔，当孔洞率为0%时，砌块均无孔洞，全部由实体材料构成，其热阻为0.80m2·K/W；当孔洞率为100%时，砌块没有实体材料，全部为填充的保温材料，其热阻为3.43 m2·K/W.

由此可扩展得到与孔洞率k相关的复合保温砌块热阻的通用计算公式：

(9)

式中：Rk为与孔洞率相关的复合保温砌块热阻，m2·K/W；λS，λW分别为实体材料和保温材料的导热系数，W/(m·K)；a为试验常数.

2.3 实体材料对热工性能的影响

选用模型M3-6和M4-6来分析实体材料导热系数λS对复合保温砌块热阻的影响.计算时，保温材料为W6，实体材料分别为S1～S6，计算结果见图4.

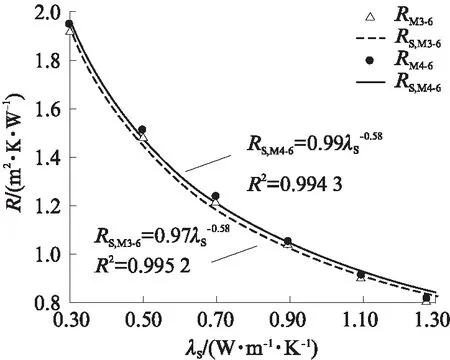
图4 实体材料导热系数对热阻的影响Fig.4 Influence of thermal conductivity of matrix material on thermal resistance

由图4可以看出，复合保温砌块的热阻随实体材料导热系数的降低而显著升高.当实体材料导热系数从1.28W/(m·K)降低到0.30W/(m·K)时，普通三排孔砌块的热阻从0.80m2·K/W增加到1.92m2·K/W，增加了140%；交错三排孔砌块的热阻从0.82m2·K/W显著增加到 1.95m2·K/W，增加了138%.按式(5)计算传热系数，普通三排孔砌块外墙由1.05W/(m2·K)降至0.48W/(m2·K)，交错三排孔砌块外墙由 1.03W/(m2·K)减小至0.48 W/(m2·K).

应用MATLAB软件对试验数据进行拟合，得到模型M3-6和M4-6的热阻与实体材料导热系数λS的关系公式，见式(10)和式(11)：

RS,M3-6=0.97λS-0.58

(10)

RS,M4-6=0.99λS-0.58

(11)

式中：RS，M3-6，RS,M4-6分别为与实体材料导热系数相关的模型M3-6和M4-6的热阻，m2·K/W.

式(10)，(11)也符合相应的极端情况：当实体材料导热系数为0时，实体材料部分的热阻趋近于无穷大，复合保温砌块的热阻也趋近于无穷大；当实体材料导热系数趋近于无穷大时，实体材料部分的热阻趋近于0，复合保温砌块的热阻也趋近于0.

2.4 保温材料对热工性能的影响

同样采用模型M3-6和M4-6来分析保温材料导热系数λW对复合保温砌块热阻的影响.计算时，实体材料为S1，保温材料分别为W1～W6，计算结果见图5.

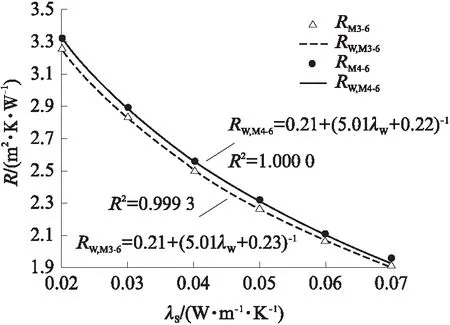
图5 保温材料导热系数对热阻的影响Fig.5 Influence of thermal conductivity of thermal insulation materials on thermal resistance

由图5可以看出，复合保温砌块的热阻随保温材料导热系数的降低而有较大的升高.当保温材料导热系数从0.07 W/(m·K)降低到0.02 W/(m·K)时，普通三排孔砌块的热阻从1.92 m2·K/W增加到3.25 m2·K/W，增加了69%；交错三排孔砌块的热阻从1.95 m2·K/W增加到 3.32 m2·K/W，增加了70%.按式(5)计算传热系数，普通三排孔砌块外墙和交错三排孔砌块外墙均由0.48 W/(m2·K)降至0.29 W/(m2·K).

应用MATLAB软件对试验数据进行拟合，得到模型M3-6和M4-6的热阻与保温材料导热系数的关系公式，见式(12)和式(13)：

RW,M3-6=0.21+(5.01λW+0.23)-1

(12)

RW,M4-6=0.21+(5.01λW+0.22)-1

(13)

式中：RW,M3-6，RW,M4-6分别为与保温材料导热系数相关的模型M3-6和M4-6的热阻，m2·K/W.

式(12)，(13)也兼顾了极端情况：当保温材料导热系数为0时，保温材料部分的热阻趋近于无穷大，但热流仍可通过实体材料部分传递，经ABAQUS软件计算，普通三排孔砌块的热阻为4.64 m2·K/W，而交错三排孔砌块的热阻为4.70 m2·K/W；当保温材料导热系数趋近于无穷大时，保温材料部分的热阻趋近于0，此时普通三排孔砌块和交错三排孔砌块的热阻均趋近于0.24 m2·K/W.

3 结论

(1)提出了复合保温砌块的设计方法，建立了孔洞率、横壁(横肋)厚度和纵肋厚度的关系式.

(2)复合保温砌块中的热流主要沿纵肋传递，横肋及其数量影响热流密度的分布；当纵肋交错排布时，局部出现热流的“断桥”现象，从而增加了复合保温砌块的热阻.

(3)复合保温砌块的热阻随孔洞率提高而增加，随实体材料导热系数降低而增加，随填充的保温材料导热系数降低而增加.通过ABAQUS数值模拟计算，得到复合保温砌块热阻与孔洞率、实体材料导热系数、保温材料导热系数的关系式，具有较高的相关性和工程指导意义.

(4)通过对240mm厚、孔洞率为60%的单排孔、双排孔和三排孔复合保温砌块的设计，使砌块热阻达到0.80～3.32 m2·K/W，即在灰缝对墙体传热影响很小时，单一砌块外墙的传热系数达到1.05～0.29 W/(m2·K)，能满足砌块和墙体热工性能大幅提升的需求.