非饱和开裂混凝土中水分运移研究

魏新江， 金立乔， 张苑竹， 丁钻辉

(1.浙江大学城市学院 土木工程系， 浙江 杭州 310015； 2.浙江大学 建筑工程学院， 浙江 杭州 310058)

水分是混凝土中物质运移的载体，水分的运移和分布直接影响着混凝土溶蚀、冻融破坏和钢筋锈蚀的速度和程度，因此研究混凝土中水分运移过程，对于分析混凝土结构的性能劣化，进行耐久性设计十分重要.

水分在孔隙介质中的运移分为饱和渗流和非饱和渗流.而混凝土事实上很难达到完全饱和.Leech等[1]通过核磁共振(NMR)技术研究了混凝土内部的相对湿度，证明了混凝土的非饱和特性；Powers等[2]通过222d浸泡试验发现长期浸泡在水中的混凝土试块也无法达到完全饱和；即便是长期承受高水压的海底隧道，取芯试验表明其服役数十年后仅在混凝土表面一定深度内达到完全饱和，超过该深度的混凝土仍处于非饱和状态[3].因此，混凝土中水分运移应该按照非饱和孔隙介质中的水分迁移进行研究.

混凝土结构通常处于带裂缝工作状态，Kermani[4]在1991年提出微裂缝会显著影响混凝土的渗透性，Aldea等[5]和Wang等[6]试验研究发现裂缝宽度大于50m或100m的微裂缝会引起混凝土渗透性的显著增长.Picandet 等[7]和Rastiello等[8]试验研究了裂缝宽度对混凝土透水性和透气性的影响，证明开裂混凝土的渗水量与裂缝宽度的立方成正比，此即符合裂隙渗流的立方定律(以下简称立方定律).王立成等[9-10]提出了混凝土细观格构网络模型，基于非饱和流体理论和立方定律，对开裂混凝土裂缝处相对含水量进行了数值分析.Zhang等[11-12]用中子检测技术对非饱和混凝土裂缝中水分早期渗透进行了试验研究.

本文基于非饱和混凝土中水分运动方程[13]和立方定律，根据双重孔隙介质模型[14]建立非饱和开裂混凝土中水分运动方程，同时通过室内渗水试验研究混凝土初始饱和度、水胶比和裂缝宽度对渗水深度的影响，采用TOUGH 2软件数值模拟非饱和开裂混凝土中水分运移流速和混凝土饱和度的变化，以期为进一步开展混凝土渗漏预测和耐久性设计提供帮助.

1 基本理论

非饱和混凝土中的水分运动可以采用Richards方程[13]描述，结合Van Genuchten-Mualem模型[15-16]，可以表示为：

u= -K(θ)ψ=

(1)

式中：u为流速，m/s；θ为混凝土含水量；K(θ)为非饱和渗透系数，m/s；为那勃勒算子；ψ为单位质量水分运动的总驱动势，Pa；Ks为饱和渗透系数，m/s；kr为相对渗透率，0≤kr≤1；s为饱和度，为残余含水量，θs为饱和含水量；m为与孔隙分布特征有关的经验参数，由试验拟合确定；ρw为水的密度，kg/m3；g为重力加速度，m/s2.

非饱和混凝土中水分等温水平运移的驱动势主要是基质势ψm，ψm与毛细吸力相关，按照Van Genuchten-Mualem模型[15-16]可以取为：

(2)

式中：α是与材料有关的经验参数，由试验拟合确定.

开裂混凝土的渗透性远大于完好混凝土，对于带单条平行裂缝的混凝土来说，其渗透系数可用立方定律来表述[9]：

(3)

将式(3)代入式(1)，可以得到非饱和开裂混凝土中裂缝处水分运动方程：

(4)

式中：uc为混凝土裂缝处水分流速，m/s.

根据双重孔隙介质模型[14]，开裂混凝土可以等效为由混凝土和裂缝2种具有不同水力参数的孔隙介质组成的复合孔隙材料.相比混凝土，裂缝具有更大的孔隙率和渗透系数，因此开裂混凝土中水分渗流问题就可以转换为水分在混凝土和裂缝这2种孔隙介质中运动的叠加.外界水分穿越裂缝入渗混凝土时，其流速在裂缝处按式(4)求解，在混凝土内按式(1)求解，在裂缝边缘式(4)，(1)满足连续条件.采用式(1)和式(4)的运动方程，结合质量守恒方程，再根据具体问题的初始条件和边界条件就可以求得混凝土各位置的饱和度s.

混凝土各点的含水量很难通过试验仪器直接检测，目前核磁共振技术、中子检测技术可以推定混凝土的含水量θ(x)，其余测试手段可以通过试块的吸水量、渗水深度等[17-18]来推定水分入渗混凝土的过程和分布.本文在试验中选用易于观察和检测的渗水深度来表征水分入渗开裂混凝土的状况，研究与混凝土初始饱和度相关的基质势、水胶比和裂缝宽度等因素对水分运移的影响，并通过数值模拟研究非饱和开裂混凝土饱和度、水分流速以及平均渗水深度的变化.

2 室内试验

2.1 试块制备

本试验配置了3种水胶比(mw/mb)的混凝土，其配合比如表1所示.其中水泥采用P·O 42.5普通硅酸盐水泥；粉煤灰采用Ⅱ级粉煤灰；细骨料选用中砂；粗骨料选用砾石，其中粒径5～10mm的含量*文中涉及的含量、比值等均为质量分数或质量比.为35%，粒径 10～25mm的含量为65%；减水剂选用聚羧酸型减水剂；水为自来水.

试验采用内部预制进水孔洞和裂缝的混凝土长方体试块(图1).试块正中的进水孔洞直径为 6mm、高度为100mm，孔洞左右两侧沿试块轴线布置有预设裂缝.试块制作利用150mm边长的立方体标准模具，在中轴线处插入8mm厚的木板进行分隔，以便同时制作2块试块.预制进水孔洞和裂缝采用φ6光圆钢筋和不锈钢薄片组成模具，在混凝土浇筑前准确定位模具，混凝土浇筑后静置至混凝土初凝前将模具平稳拔出.试块浇筑2d后拆模送至(20±2) ℃、相对湿度大于95%的养护箱中养护28d.

表1 混凝土试块配合比

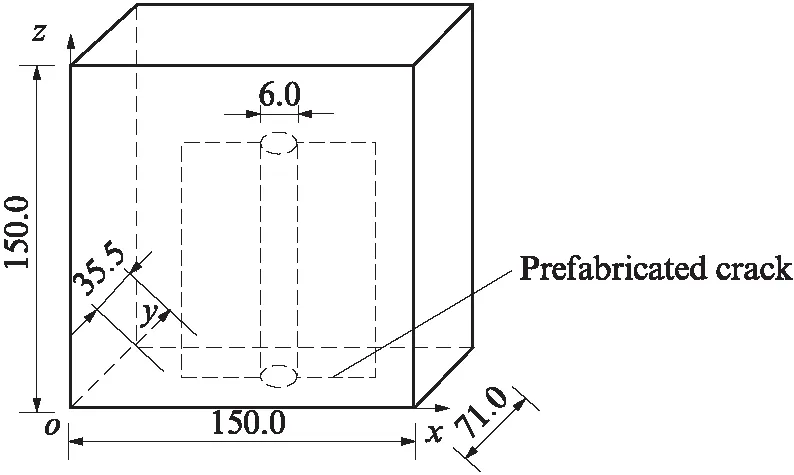
图1 开裂混凝土试块示意图Fig.1 Schematic diagram of cracked concrete specimen(size：mm)

为了保证试验时试块的预制孔洞为唯一进水通道，试验前先将与压力室接触的试块底面打磨，然后用环氧超能胶封闭裂缝.完成渗水试验后将试块在万能压力机上垂直于预制裂缝高度的1/2处(z=50mm)进行劈裂，然后采用FTLF-2型裂缝测宽仪(量程8mm，精度0.01mm)测量试块的实际裂缝宽度.测量发现裂缝宽度实测值都在预制值附近波动，这是因为不锈钢钢片较薄，拔出时对预制裂缝周围的混凝土会产生扰动，拔出后混凝土又会自行闭合.总体而言，w=0.3mm 时的预制情况好于w=0.1mm 和w=0.5mm时，但实测裂缝宽度的绝对误差值均未超过0.1mm，满足本试验对裂缝宽度的预制要求.

2.2 室内试验

2.2.1试块的初始饱和度

为了研究基质势ψm对非饱和开裂混凝土中水分运移的影响，本试验设计了3种初始饱和度：自然状态以及在105℃烘箱中烘0.5，8.0h.

先用电子天平称量混凝土试块，记录试块自然状态下的初始质量m0；再将试块放入105℃烘箱中干燥至恒重,记录残余质量mr；然后将烘干的试块完全浸没于水中，每天称重直至其质量不再变化，记录完全饱和质量ms；将完全饱和试块放入105℃烘箱中分别烘0.5，8.0h，记录试块在这2种初始饱和度状态下的初始质量m0；最后按式(5)计算混凝土在3种初始质量下的初始饱和度s0，结果如表2所示.

(5)

2.2.2试验步骤

本试验采用智能控压渗透装置进行开裂混凝土渗水试验.该装置包括储水罐、数字控制压力表、增压泵、传感器和管道.试验前先将开裂混凝土试块的预制孔洞与压力室出水口对齐，在控制压力表上设定好水压P0和加压时间t后开启渗透装置的水阀，增压泵提供压力推动储水罐内的水通过试块的预制孔洞和裂缝入渗开裂混凝土.当达到各试验工况(表2)预定加压时间后取出试块，用万能压力机劈裂试块，然后采用游标卡尺分别量出沿裂缝方向和垂直裂缝方向的渗水深度.

表2 试验工况表

3 结果分析与讨论

3.1 开裂混凝土试块的渗水深度

从试块劈裂后的渗水图(图2)可以看出：水分沿预制孔洞和裂缝成梭形入渗分布，沿裂缝方向的渗水深度远大于垂直裂缝方向的渗水深度，说明混凝土裂缝处渗透性高于未开裂处.

图2 试块劈裂后的渗水图Fig.2 Penetration figure of specimen after split

以工况1～4为例，将12，24，48，72 h沿裂缝方向和垂直裂缝方向的渗水深度描点连线，示意水分在1/2试块中的渗水轨迹(图3).由图3可以看出，2个方向的渗水深度随时间延长而增长，沿裂缝方向的渗水深度基本等于裂缝长度(30mm)与垂直裂缝方向的渗水深度之和，因此可以认为压力水从预制孔壁入渗混凝土后迅速沿裂缝方向渗透到裂缝底端，并进一步向混凝土内部入渗，与垂直裂缝方向的入渗速率基本同步，渗水深度相当.在后续分析中，各工况下的渗水深度取沿裂缝方向左右的裂缝底端渗水深度平均值.

图3 工况1～4的渗水深度分布Fig.3 Distraction of penetration depth of working conditions 1-4

图4 不同初始饱和度下试块的渗水深度Fig.4 Penetration depth of specimens under different initial saturation degrees

3.2 初始饱和度的影响

在不同初始饱和度条件下(工况1～12)开裂混凝土试块的渗水深度如图4所示.由图4可以看出：混凝土初始饱和度越小，渗水深度越大，反映出与初始饱和度对应的毛细吸力是水分运动的主要驱动力；混凝土初始饱和度越小，渗水深度随着加压时间的延长增长越快，即入渗速率越大.这是因为压力水穿过预制孔洞壁和裂缝壁入渗非饱和混凝土试块时，孔洞壁和裂缝壁存在饱和进水面层，此处驱动总势ψ(x=72mm)=ψ(x=78mm)=ψ0=0.3MPa；而紧邻的混凝土处于非饱和状态，驱动总势ψ=ψm.从式(2)可知，s0越小则ψm越小(其绝对值越大)，相应的ψ=ψ0(x=72mm)-ψ(x<72mm)或ψ=ψ0(x=78mm)-ψ(x>78mm)越大．从式(1)可知，s0越小则水分流速越快，导致水分入渗流量越大，饱和度增长越快，与试块初始饱和度的差异越明显，渗水深度也越大.

从图4还可以看出，随着加压时间的增加，s0=0.32，0.72时混凝土的渗水深度斜率总体逐渐趋于平缓.这是由于随着饱和度s的提高，基质势ψm逐渐提高，在水压(P0=0.3MPa)不变的条件下ψ逐渐减小，因此从式(1)和式(4)可判断此时水分流速也逐渐下降.

3.3 水胶比的影响

不同水胶比条件下(工况1～4,13～20)开裂混凝土试块的渗水深度见图5.由图5可以看出：混凝土水胶比越小，渗水深度越小，这是由于水胶比越小混凝土越致密，孔隙率越小，因此水分越不容易渗入.

图5 不同水胶比下试块的渗水深度Fig.5 Penetration depth of specimens under different water binder ratios

3.4 裂缝宽度的影响

不同裂缝宽度条件下(工况1～4和21～28)开裂混凝土试块的渗水深度见图6.由图6可以看出，混凝土预制裂缝宽度越大，渗水深度越大.根据式(4)，裂缝宽度w越大，水分流速uc越快，因此水分入渗流量越大，混凝土饱和度s增长越快，s与试块初始饱和度s0的差异越明显，渗水深度也越大.但w=0.1mm和w=0.5mm时的试验结果规律性不如w=0.3mm时，这可能与预制裂缝宽度的误差有关.

图6 不同裂缝宽度下试块渗水深度Fig.6 Penetration depth of specimens under different crack widths

4 数值模拟

4.1 数值建模

图7 模型网格划分Fig.7 Mesh diagram of the model

4.2 分析与讨论

4.2.1饱和度的变化

以工况1～4为例，数值分析得到非饱和开裂混凝土的模拟饱和度分布云图，如图8所示.由图8可见，裂缝处由于渗透系数较大而首先达到饱和，随后模拟饱和度沿着裂缝和进水面逐渐提高，反映出水分向混凝土内部运移，饱和度分布形状与试验获得的渗水形状(图2)相似.

以工况1，4和工况5,8的参数建模，数值分析不同初始饱和度条件下非饱和开裂混凝土单侧模拟饱和度的变化，图9是x=60mm处模拟饱和度的数值分析结果.由图9可以看出：当t=12h时，裂缝附近水分饱和度已接近完全饱和，而模型远端的饱和度还基本等于初始饱和度s0；当t=72h时，整个模型接近完全饱和；s0=0.32模型从模型远端s=s0

图8 工况1～4下非饱和开裂混凝土的模拟饱和度云图Fig.8 Simulated saturation profiles of cracked unsaturated concretes under working conditions 1-4

图9 不同初始饱和度下非饱和开裂混凝土 单侧模拟饱和度Fig.9 Simulated saturations of cracked unsaturated concretes under different initial saturations (one side)

增长到s=1的速度快于s0=0.72模型，但由于两者的初始饱和度相差较大，s0=0.32模型的整体饱和度还是小于后者，这一规律与文献[9]中的数值模拟结果吻合.如果用水分完全饱和区范围来表征渗水深度，则不能反映3.2节中初始饱和度越低渗水深度越大的试验现象．本文认为试块上显现的渗水深度应该与试块的初始饱和度相关，水分入渗后混凝土饱和度s与s0的差值越大，则渗水深度越大.

4.2.2流速的变化

以工况1，4，5，8，21，24的参数建模，数值分析不同初始饱和度和裂缝宽度下模型内水分流速的变化，结果见图10.从图10可以看出：由于裂缝左右两侧水分流动方向相反，因此流速呈现以裂缝为对称轴的反对称分布；在裂缝边缘，由于水分是从渗透性大的裂缝区域进入渗透性小的混凝土区域，因此流速增长最大；离裂缝越远，流速越小.从图10还可以看出：s0越小则流速u越大；w越大则流速u越大，流速曲线与横坐标围成的面积越大，相应的平均流速越高；随着加压时间的延长，近裂缝处最大流速逐渐下降，而远离裂缝处流速有所提高，总体趋势是模型内流速差趋缓，平均流速随加压时间延长而逐渐降低.流速是混凝土饱和度增量的函数(见式(1))，这也可以解释4.2.1节模拟饱和度的变化规律，并与3.2节的试验规律吻合.

图10 不同初始饱和度和裂缝宽度下非饱和 开裂混凝土的模拟流速Fig.10 Simulated flow velocity of cracked unsaturated concretes under different initial saturations and different crack widths

图10模拟得到的流速小于文献[18]中完好混凝土的模拟流速，原因是后者建模时压力水直接施加在150mm高的孔壁范围，而本模型中压力水只作用在d=6mm的半圆形进水面范围.

4.2.3渗水深度的变化

根据文献[20]，混凝土中渗水深度可用水分平均流速与入渗时间求解，即：

(6)

式中：S为在时间T内的渗水深度，m.

根据4.2.2节的模拟流速，按式(6)计算得到不同初始饱和度和裂缝宽度下的渗水深度，见图11.由图11可见：非饱和开裂混凝土初始饱和度越低，渗水深度越大；裂缝宽度越大，渗水深度越大，而且渗水深度增长符合先快后慢的特点，这是由于入渗平均流速随着加压时间的延长而逐渐下降所致.

图11 不同初始饱和度和裂缝宽度下的模拟渗水深度Fig.11 Simulated penetration depth under different initial saturations and crack widths

5 结论

非饱和开裂混凝土的初始饱和度越小、裂缝宽度越大，则渗水深度越大，渗水深度增长先快后慢，反映出非饱和混凝土的基质势是驱动水分运移的主要因素，并且裂缝宽度与混凝土渗透性正相关.采用本文建立的非饱和开裂混凝土中水分运动方程可以合理地解释试验结果.另外，数值分析发现水分入渗开裂混凝土后流速差和平均流速随时间延长逐渐降低，采用平均流速计算渗水深度可以较好地反映渗水试验中渗水深度的变化规律.