矿物组分分布对花岗岩力学性质影响的PFC模拟分析

2018-11-02陈世江郭国潇肖永健

中国钨业 2018年4期

陈世江，郭国潇，肖永健

（1.内蒙古科技大学矿业研究院，内蒙古包头 014010；2.华电内蒙古能源有限公司土默特发电分公司，内蒙古包头 014100）

CHEN Shijiang1,GUO Guoxiao1,XIAO Yongjian2

(1.Inner Mongolia University of Science and Technology Institute of Mining,Baotou 014010,Inner Mongolia,China;2.Huadian Inner Mongolia Co.,Ltd.,Tumote Power Generation Branch,Baotou 014100,Inner Mongolia,China)

岩石的力学性质是工程岩体分类、岩石工程设计的基础。大量的岩石力学试验表明，岩石试样的物理力学参数存在离散性。造成这种离散性的原因，除了试验条件的因素外，更重要的是岩石矿物组成、微构造等自身非均质性的缘故。由于岩石矿物组分、微构造分布的复杂性，即使是同一岩样，在不同方向表现出的力学性能也不一样[1-6]，即岩石力学性质存在各向异性特征。为了探究岩石力学性质的各向异性特征，王家兴[7]等人对石英云母片进行了单轴抗压试验，选取不同荷载与片理夹角3组试样，对试样的各向异性特征进行试验研究，试验结果表明，不同片理角度试样的强度差值较大，试样单轴抗压强度值跨度较广。闫小兵[8]等人对地壳岩石进行了一系列试验研究，试验结果表明，不同样品的变异性程度变化较大，这主要受到样品中的孔隙的含量、裂隙的形态与分布的控制。岩石不同方向的强度和岩石中云母的含量呈定向正相关关系，这表明酸性岩石的各向异性大小在很大程度上受到岩石中云母含量以及定向程度的控制。岩石力学试验是破坏性的，不能重复进行，因此上述探讨并非完全意义上岩石各向异性特征的研究，但研究结果给了研究者很好的启示。我国大部分产钨矿山中钨矿田的形成与分布广泛的花岗岩密切相关，主要矿床多产于花岗岩岩体或花岗岩围岩接触带中[9]，所以对花岗岩各向异性特性的试验探索对由花岗岩组成的矿脉或围岩的性质研究具有部分指导意义。

研究基于颗粒流理论[10-11]，借用PFC数值模拟软件建立单轴压缩试验模型，通过参数调试得到与室内试验宏观力学参数相匹配的细观力学参数，并以此为基础，对6组数值模型进行单轴压缩模拟试验，研究其在矿物组分含量相同而分布不同的情况下，模型宏观力学性质的差别及其各向异性特征。

1 单轴抗压强度各向异性数值模拟

图1为花岗岩单轴试验示意图（图（b）为图（a）顺时针旋转90°后所得）。该试件从不同的方向进行加载，其力学性质是不同的，这是因为岩石各物质组分虽相同，但在加载方向上，各物质组分及其内部微构造的分布是不同的，因此，研究欲应用PFC数值模拟方法，通过控制物质组分含量，改变其分布特征，来实现岩石单轴抗压强度各向异性的探究。

图1 各向异性花岗岩单轴试验示意图Fig.1 Anisotropic granite uniaxial test schematic

数值模拟模型尺寸与室内试验试件尺寸一致，选用50 mm×100 mm的模型尺寸。进行数值模拟试验时，首先生成模型墙体并在墙体内生成颗粒；然后添加黏结模型且达到初始平衡；再通过给墙体赋予速度，模拟单轴压缩加载过程。与此同时记录整个试验过程中颗粒与墙体的位移、不平衡力，再通过内置编辑的FISH函数等后处理方式得到模型宏观破坏过程中的各类数据及力学参数，如图2所示。

图2 模拟加载示意图Fig.2 Simulated loading diagram

2 细观模型力学参数值的确定

2.1 接触模型的选用

模拟岩石类材料，需要设置黏结模型来表征颗粒之间有类似胶结物的存在。选用平行黏结模型（PBM model）来模拟模型的加载，平行黏结模型颗粒间的黏结破坏后会立即导致模型整体宏观强度的下降，这样与岩石类材料真实破坏过程更贴近。

2.2 矿物组分含量的确定

在进行花岗岩室内试验前，应用数码相机获取花岗岩试件图像。对一组3个试件随机单独抽取的图像使用Matlab灰度图像统计分析，通过分割阈值为 80、165 将像素区间划分为 0～80、81～165、166～255（255为白色，0为黑色），将细观组分分为三类，分别为云母、长石、石英，如图3所示。再对统计数据进行归一化处理，最后得到花岗岩各组分比例。因最后选取的室内试件为第2组试件，所以得到的花岗岩各组分比例为11%的云母、62%的长石、27%的石英。

图3 花岗岩数字图像Fig.3 Granite digital image

2.3 细观力学参数值的确定方法

因为PFC数值模拟需采用颗粒和黏结的细观力学参数来共同表征数值模型的宏观力学性质，且这些细观力学性质参数无法从实验室直接获取，因此在模拟试验开始之前要对模型的细观物理力学性质参数进行标定。

对于花岗岩各组分之间力学性质参数的比例关系问题，国内的一些学者，如李进昭[11]以及徐金明[12]等人已经做过大量研究工作，得到了一系列花岗岩各组分之间力学性质参数比例关系较为合理的参数。根据文献中所给出的数值参数建议，再对数值模拟模型进行一系列“试错”试验[13-14]，反复改变颗粒与黏结的细观参数，直到数值模拟试验得到的细观力学参数与室内宏观力学参数值相匹配时即表示细观参数调试完成。

室内试验使用的机器是万测（WANCE）微机控制电液伺服万能试验机，选用了一组三个50 mm×100 mm的花岗岩试件进行单轴压缩试验，室内试验如图4所示。在三个试验结果中选取了一个试验效果较好的花岗岩试件进行试验数据处理，获得的宏观物理力学性质值为：单轴抗压强度σ=124.6 MPa，弹性模量E=41.3 GPa，然后在数值模拟程序中通过“试错法”[15]多次调整对比并考虑各组分之间的物理力学参数比例关系，使得数值模拟模型得到的宏观力学参数贴近于室内试验中花岗岩的宏观力学性质参数值，最后确定该模型的各项细观力学性质参数，如表1及表2所示。

图4 花岗岩室内试验图Fig.4 Granite indoor test chart

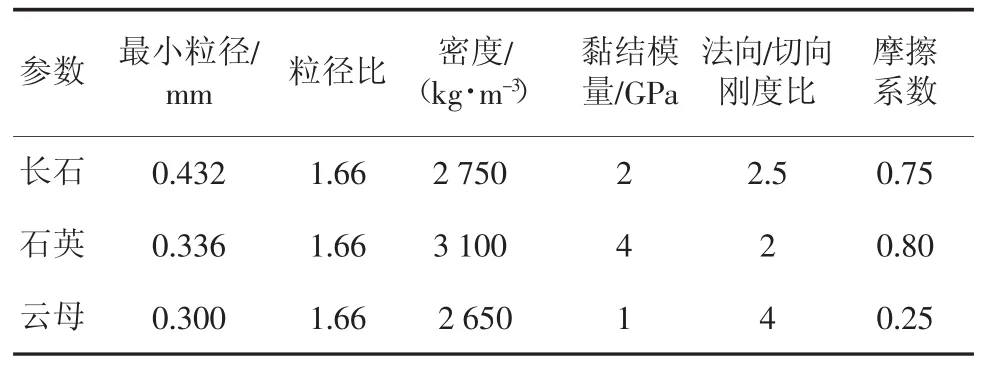
表1 颗粒单元的细观参数Tab.1 Microscopic parameters of particle units

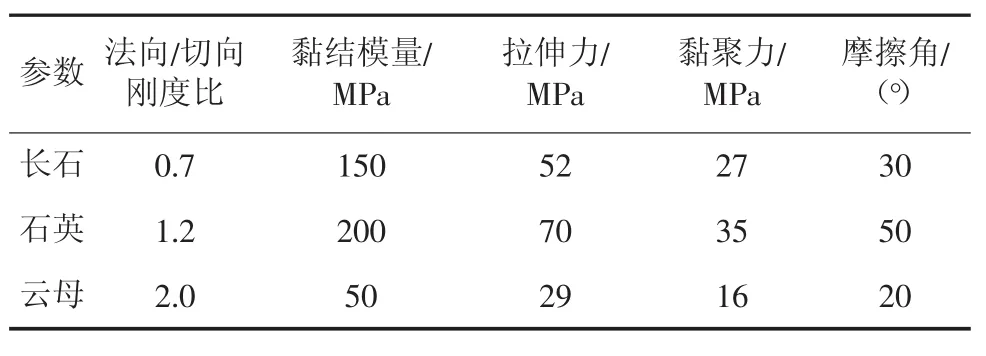
表2 接触黏结模型的细观参数Tab.2 Microscopic parameters of the contact bonding model

2.4 数值模拟模型与室内试验的宏观参数对比

将最后确定的模型各项细观力学性质参数应用于数值模型中，并进行单轴压缩模拟试验，得到模型的应力-应变曲线，两组试验的应力-应变曲线如图5所示。数值模拟试验与室内试验的应力-应变曲线存在略微偏差，但整体呈现出来的趋势比较一致，且因为室内试验电阻应变片在岩石崩坏时已破坏或脱落，所以岩石的峰后残余强度特征不明显。

经计算后，PFC数值模拟模型的力学性质参数与室内试验力学性质参数对比见表3。由表3和图5可知，数值模型与室内试验的宏观力学参数结果吻合较好，可以使用这组细观力学参数组成的数值模型来近似模拟所选取的室内花岗岩。

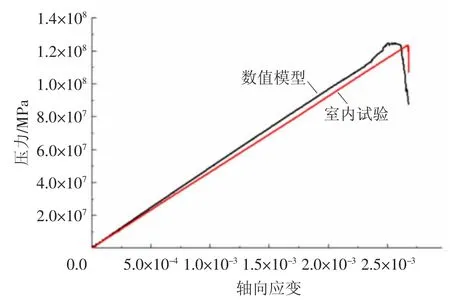
图5 匹配应力-应变曲线Fig.5 Matched stress-strain curve

表3 数值模型与室内试验的力学参数对比Tab.3 Comparison of mechanical parameters between numerical models and laboratory tests

3 花岗岩单轴抗压强度的各向异性模拟试验

为了研究同一岩样单轴抗压强度的各向异性特征，数值试验在固定矿物组分含量相同的情况下，通过改变颗粒分布随机数来实现岩样组分分布的改变。总共建立了6组数值模型，且保证不同模型之间只有颗粒分布随机数不同，其他所有细观力学参数都相同，然后再对6组数值模型分别进行单轴压缩模拟试验。

3.1 相同组分含量、不同分布模型的生成方法

相同组分：通过颗粒级配方法，固定百分比生成三种组分颗粒。

不同分布：通过改变颗粒分布随机数，从而使得颗粒分布改变。

6组数值模型的应力-应变曲线及最终破坏模型如图6所示。图中横坐标为纵向应变的值，纵坐标为纵向应力的值。feldspar对应长石，颗粒颜色为灰色；mica对应云母，颗粒颜色为黑色；quartz对应石英，颗粒颜色为白色。

经统计计算，得到各颗粒模型的宏观力学性质参数见表4和图7。由图6、图7和表4可知，在相同矿物组分但矿物分布不同的情况下，各颗粒模型之间的单轴抗压强度值差别较大，模型的单轴抗压强度值最大可达到134.15 MPa，最小的单轴抗压强度为113.73MPa，相差20.4 MPa。而各模型的弹性模量值变化不大，基本稳定在39.50 GPa左右。

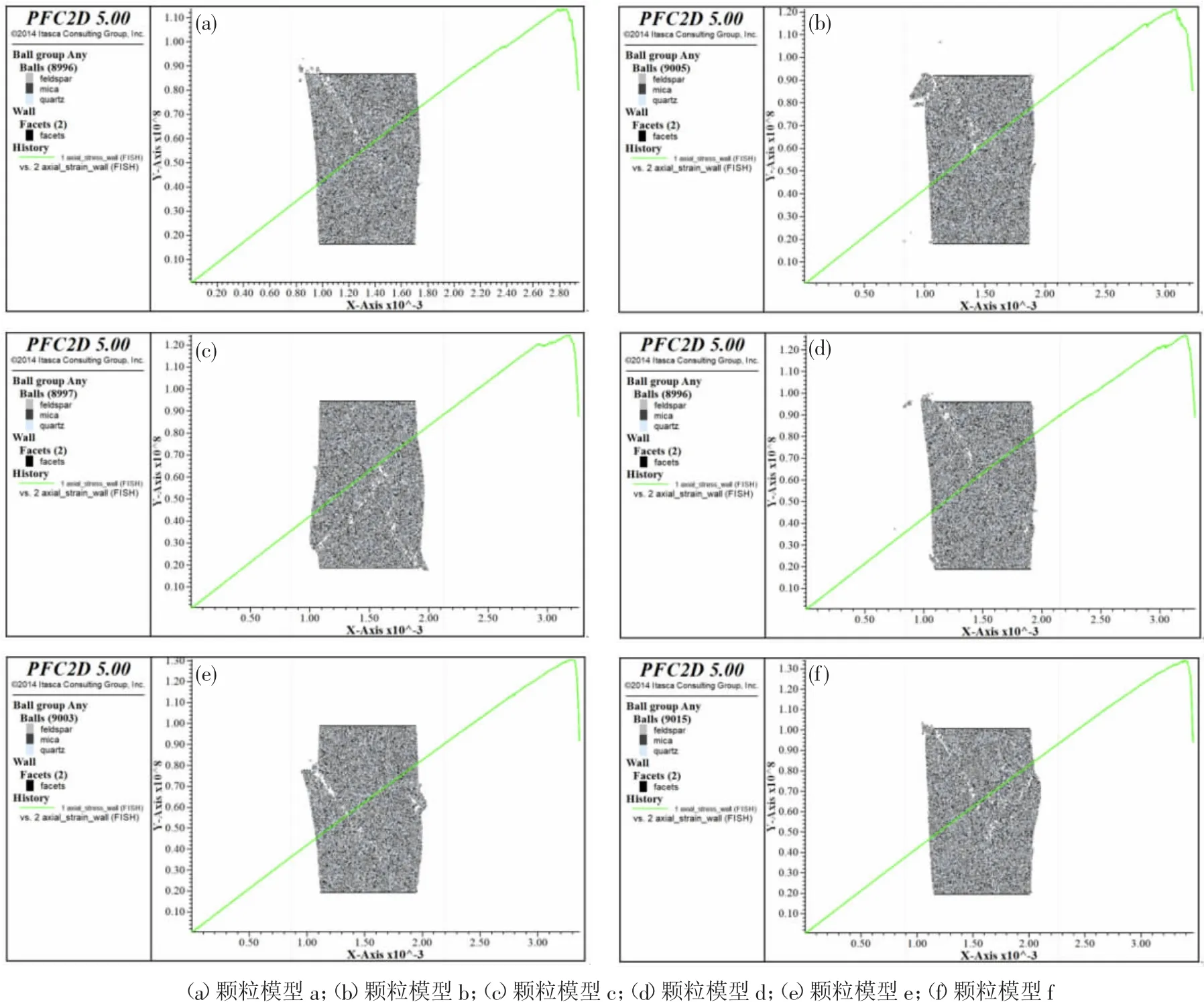
图6 矿物颗粒不同分布模型的应力应变曲线和破坏模型图Fig.6 Stress-strain curves and failure model diagrams for different distribution models of mineral particles

图7 6组颗粒模型应力-应变曲线Fig.7 Stress-strain plots for six groups of particle models

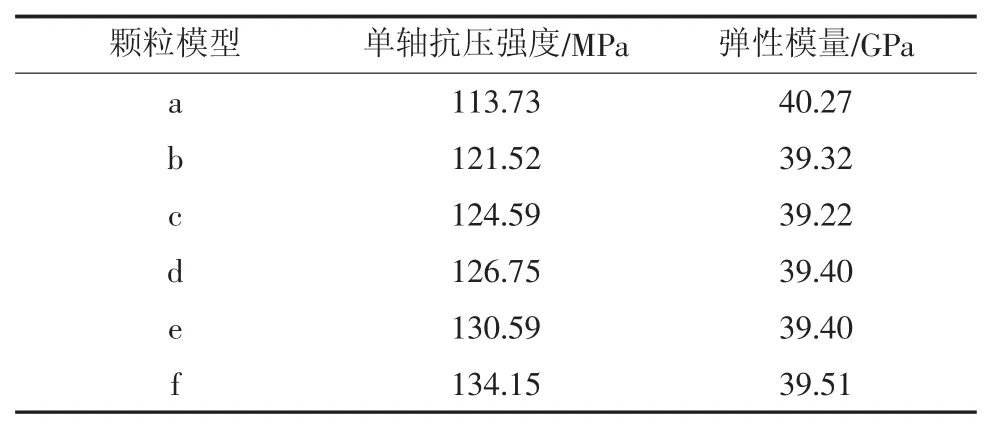
表4 各颗粒模型的宏观力学参数Tab.4 Macro-mechanical parameters of each particle model

3.2 数值模型破裂分析

对6个数值模型加载各个时期的模型图进行观测分析，发现所有模型基本都是从上下两端部开始破坏，然后逐渐贯通发育为宏观大裂隙；破坏区基本都是在云母（黑色颗粒）成分较为密集的区域开始发展，云母相对于其他两种组分（长石、石英）来说物理力学性质较差，其集中区易遭破坏，所以云母集中的区域最先发生破裂；云母分布越集中的模型其强度越低，云母分布越分散的模型强度越高，说明云母的分布情况影响数值模型的强度及其破坏样式，进一步说明了岩石材料的宏观力学特征是其内部材料的细观力学特性的综合反映、印证了岩石细观分布结构控制其宏观破坏模式这一论点。