Lingo法在装配线平衡设计中的应用

贾舒媛，田亚凤，彭玲玲，杜 倩，顾永虎

（攀枝花学院，攀枝花 617000）

1 现有装配线问题分析

企业要想提高产量，降低成本，其装配线的平衡设计是必不可少的。本课题选用电风扇的装配线为研究对象。实地调查，对该企业风扇装配线的具体的流程进行了考察和记录。对各个工序进行作业时间的测定，本文采用秒表时间研究法测定计算每道工序的作业时间，运用三倍标准差法进行异常值的剔除，最后计算每道工序的算数平均数作为每道工序的实际操作时间。评比系数为1，宽放系数为0.1，则经过计算后，得出装配线上各工序标准作业时间，如表1所示。考虑到企业工艺要求，表1中各工序名称不在此陈述，不影响本文研究。

公司日工作时间为8小时，该装配线日产量在670台，生产节拍为37秒，装配线有24个工位，每个工位有一名操作者。该生产线平衡率=各工序时间之和/（瓶颈工序×工序数）×100%=523/（37×24）×100% =56.66%。可以看出，目前该装配线不平衡，非瓶颈工序等待时间较长，瓶颈工序半成品堆积较多，且现有装配线工位有24个，占地面积大，故该装配作业线急需平衡改善。

2 Lingo模型的建立与求解

本文将用Lingo法在不改变产品工艺流程的情况下，对装配线进行装配线平衡设计，通过该方案的平衡优化设计，愿求得一个平衡率更高的装配线。

2.1 数学模型的建立

Lingo主要是求解数学函数，因此在进行lingo程序的编制之前，应将平衡问题转换成数学模型，我们先给出以下定义：

C为装配线节拍；K为工位的数量；k代表第k个工位；

Tasks={1，2，…，}作业工序的集合；其中m为作业工序个数；I，j为作业工序的序号；

ti为第i个工序的作业时间；

Pred为作业工序的顺序合集，既前置工序与后置工序的关系合集。

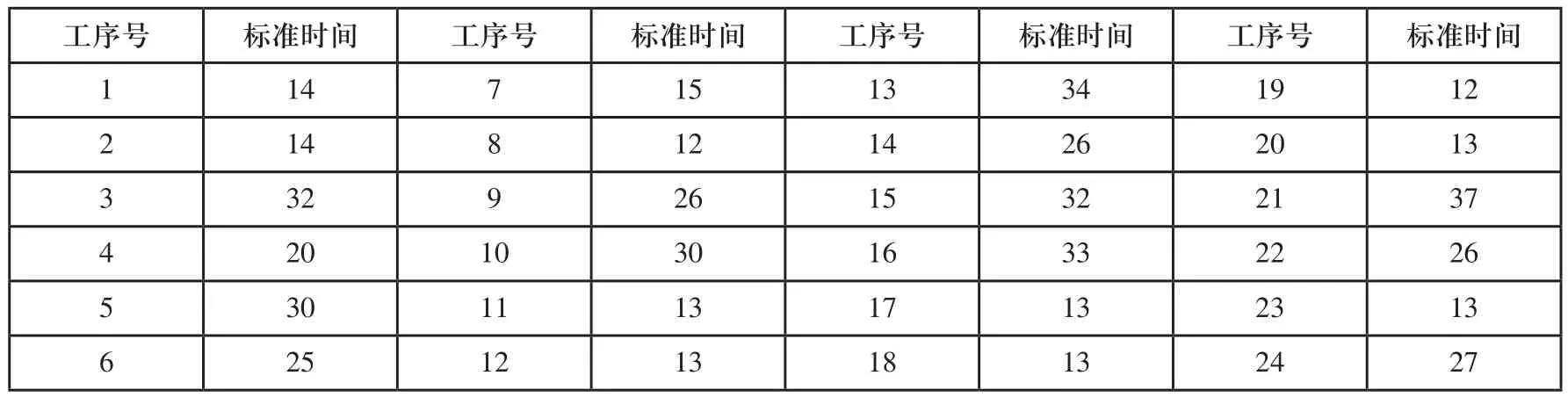
表1 工序对应表（时间单位：秒）

进行上述定义之后，我们将平衡问题转换为数学的函数模型。对于第II类平衡问题，需要优化的是装配线节拍，尽量在要求工位数量下使得节拍最小，因此其目标函数为：

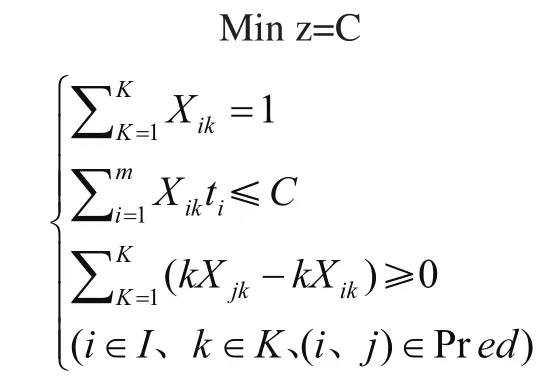
其中Min z=C为目标函数，追求整条流水线节拍最小。

2.2 程序的编制与求解

前文我们已将数学模型建立完成，根据数学模型编制的Lingo程序如下所示：

将程序输入Lingo程序，本次求解程序运行52秒得出本次Lingo的平衡求解的最优解，最优节拍为46秒，将其处理总结绘制成如表2所示的表格。

图1 Lingo模型求解时间柱形图

表2 Lingo模型求解结果

将程序输入Lingo程序，得出本次Lingo的平衡求解的最优解，最优节拍为46秒，根据各个工位的作业时间，绘制出各个工作站的平均符合图画出工位的作业时间图如图1所示。根据图1可以看出，工位1、工位7、工位9的作业时间最长为46s，工时最短的工位为13工位，作业时间为27s，工作站的作业时间最长和最短之间相差19s。该方案平衡率=523/（46×13）=87.4582%，平衡率超过了85%，说明平衡效果水平“良好”。

2.3 方案对比

本节将计算和评比上述方案的关键指标。

1）平衡率：

2）平滑指数SI：

3 结束语

本课题对某小家电有限公司的家用电风扇装配线深入研究，找出了其存在的主要问题，通过Lingo软件建模得到装配线平衡方案，通过关键指标评价该方案。该方案使产线平衡率得到很大提高，平衡性能达到良好级别，也使整个装配线负荷更均匀。通过装配线优化设计完成装配模式的改变，为实现均衡生产提供条件。