基于扩展卡尔曼滤波的小型无人机锂电池组SOC估计
2018-11-02王顺利谢滟馨
张 丽,王顺利,陈 蕾,苏 杰,谢滟馨
(西南科技大学 信息工程学院,绵阳 621010)
0 引言
小型电动无人机由于其体积小、重量轻、机动灵活和成本低等特点,广泛应用于军事和民用方面[1]。动力电池是小型无人机最关键部分。锂电池因具有自放电率低、能量密度高和使用寿命长等优点成为小型无人机的首选电源。于是管理小型无人机动力锂电池成为必要,而管理锂电池的最核心内容之一是对锂电池SOC进行估算。
电池的SOC是指电池的剩余容量与其完全充电状态的容量的比值。它不能被直接测量,只能通过测量电池的电流和电压等物理量来估算SOC。因为实际应用中传感器测量到的电压、电流等数据都受到噪声的污染,而传统的SOC估算方法如安时积分法、开路电压法等估算方法对降低噪声效果不理想,所以存在误差大,难以实时估算电池的SOC等缺点。
卡尔曼滤波算法[2]是处理噪声的利器。经典卡尔曼适用于线性领域。小型无人机锂电池SOC是一种非线性系统,经典卡尔曼滤波算法不适用,因此本文采用扩展卡尔曼算法对电池SOC进行估算。
通过搭建小型无人机锂电池测试平台,将本文的算法进行了实验应用测试,验证了该算法的有效性。结果表明,该方法可使状态估计值具有较小的误差和快速跟随性,基本满足了对小型无人机锂电池SOC估计的需求。
1 理论分析
1.1 锂电池状态模型及其参数辨识研究
精确的电池模型对电池的SOC估算至关重要。目前常用的电池模型有电化学模型[3]、人工神经元网络模型[4]、等效电路模型等。电化学模型一般适用于锂电池的研发和改进阶段,不适用于电池管理系统的研究。人工神经元网络模型需要大量的实验数据,对电池历史数据依赖性太大,也不适合本文的研究。
典型的电路模型有Rint模型、Thevenin模型[5]、PNGV模型[6]和Massimo Ceraolo模型等。对比分析发现,Thevenin模型既可以很好地表示电池端电压的突变型,又可以表现其渐变性,而且计算量规模合适。所以本文采用Thevenin模型。电池Thevenin模型如图1所示。
该模型将锂电池等效为由电动势E、欧姆电阻R0、极化电阻R1、极化电容C、电池电流i和端电压V组成的模型。该模型有如下电气关系。

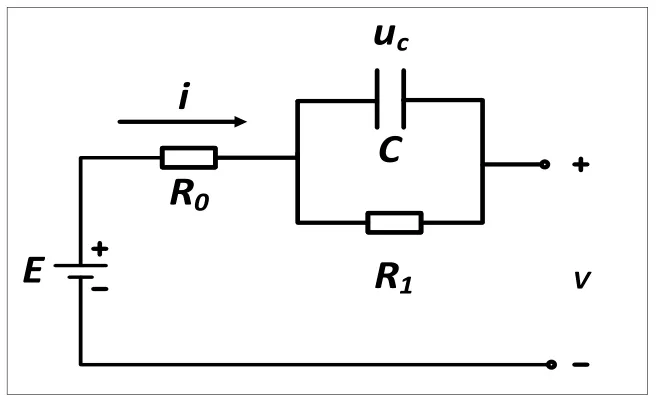
图1 小型无人机锂电池组戴维南模型
如式(1)所示。式(1)的第一部分和第二部分分别是Thevenin模型的KVL和KCL关系。
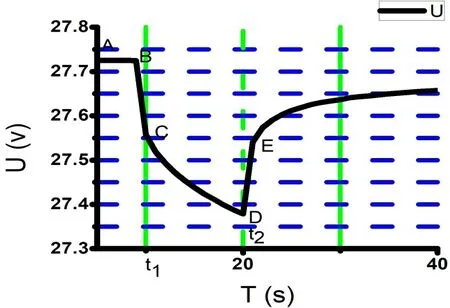
图2 钴酸锂电池组HPPC实验曲线示意图
一般进行混合动力脉冲能力特性实验[7](Hybrid Pulse Power Characteristic,HPPC)来辨识模型中的各个参数。如图2所示。
图2中BC段电压突变是由于电池欧姆内阻R0引起的,欧姆内阻。CD段电压变化表现的是极化内阻,极化内阻1。针对模型中的RC一阶电路,时间常量是一个常量,,于是极化电容
1.2 锂电池SOC估算方法研究
估算锂电池SOC的方法有很多种,比较典型的方法有安时积分法、开路电压法、放电实验法、神经网络法和卡尔曼滤波法[8]等方法。
开路电压法是用电池的开路电压U来估算电池的SOC。U-SOC的函数关系可表示为Ut=F(SOCt)。通过测量电池的开路电压,通过U-SOC关系式确定电池SOC。但是锂电池工作状态下难以获得准确的开路电压,所以该方法误差较大。
安时积分法是根据SOC的定义来估算,SOC的定义式如式(2)所示。
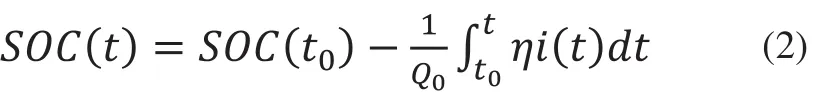
一般取电池满电时刻为t0,此时有电池标称电容Q0,η是一个补偿电池放电倍率、温度和电池健康状态等对SOC的影响。因为工作状态下获取锂电池充放电电流存在误差,所以SOC估算也存在较大误差。
放电实验法相当可靠,但是对人力物力消耗大,不能在线估计,一般用于实验研究。神经网络法需要大量训练数据,对历史数据依赖大,计算量大,测量精度会严重影响估计精度。
应用卡尔曼滤波算法估计锂电池SOC,具有精度高和实时性好等优点。本文将锂电池极化电压uc和SOC作为系统状态量,电流i作为系统输入量,然后构建状态方程和观测方程,再对方程进行离散化和线性化,最后应用卡尔曼算法多SOC进行估计。
1.3 扩展卡尔曼算法研究
卡尔曼滤波算法是一种利用线性状态方程,通过系统输入输出数据,对系统当前状态进行估计的一种算法。因为卡尔曼滤波算法完全是在时域进行估算,没有进行时域和频域的相互转换,所以计算量小,实时估计效果相当好。经典卡尔曼算法适用于线性系统,而锂电池SOC系统是非线性的。扩展卡尔曼算法是对经典卡尔曼算法的改进。它是把非线性空间方程通过泰勒展开,舍去二阶及以上项得到近似的线性空间方程,然后对线性空间方程应用卡尔曼滤波算法,从而估算当前空间状态的一种算法。它适用于离散非线性系统。
离散非线性系统空间可表示为:

式(3)第1部分表示状态方程,第二部分表示观测方程。K是离散时间,Xk+1是n维状态向量,Zk是m维观测向量,Wk和Vk是相互独立的高斯白噪声。为了应用卡尔曼滤波,对非线性函数f(*)和h(*)围绕进行一阶泰勒展开。展开结果如式(4)所示。

对式(4),令:
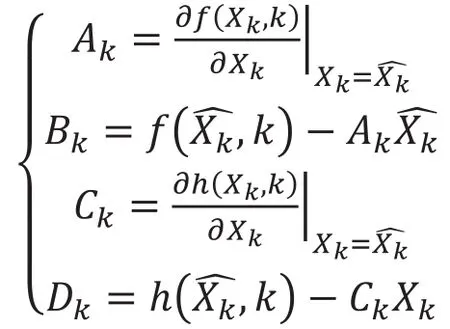
则式(4)可以线性化为:
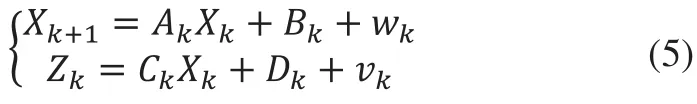
对线性化后的模型(5)应用Kalman滤波基本方程便得到扩展Kalman滤波的递推过程。

式(6)中,P是均方误差,K是卡尔曼增益。I是n×m单位阵。Q和R分别是w和v的方差,一般不随系统变化。
滤波初值和滤波方差分别为X(0)=E[X(0)],P(0)=var[X(0)]。(K+1)周期中滤波步骤如下。先由k时刻的状态和均方误差估算当前时刻的状态和均方误差得到先验状态和先验均方误差,然后计算当前时刻的卡尔曼增益Kk+1。最后用Kk+1修正先验状态得到当前时刻的状态,并且修正先验均方误差得到当前时刻的均方误差。
2 实验验证
本文采用小型无人机常用的钴酸锂电池进行实验验证。该电池单体额定电容4Ah,额定电压3.7V,工作电压范围3.7~4.15V。为了高仿实际工况下的小型无人机锂电池组工作状态,本文采用串联7节4Ah钴酸锂电池单体的锂电池组进行实验验证。
2.1 E-SOC关系曲线实验
在不同SOC下静置40分钟,然后测得开路电压,此时开路电压与锂电池电动E势相等。然后对E-SOC数据进行7阶多项式拟合。得到的E-SOC曲线如图3所示,E-SOC关系如式(7)所示。
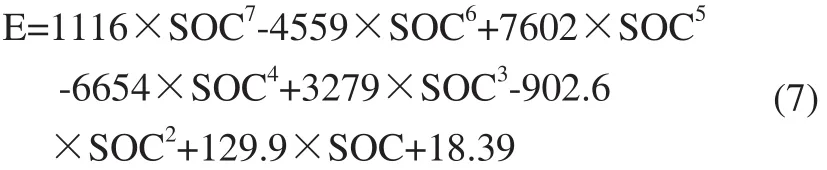

图3 钴酸锂组电池E-SOC曲线
2.2 模型参数辨识实验
本文通过进行混合动力脉冲能力特性实验(Hybrid PulsePower Characteristic,HPPC)来确定模型的参数。本实验共设置9个采样点采集各参数与SOC的关系。分别采集SOC从100%到10%的数据,SOC每变化10%采集一次数据。充电和放电各做一次,取两次的均值。数据如表1所示。
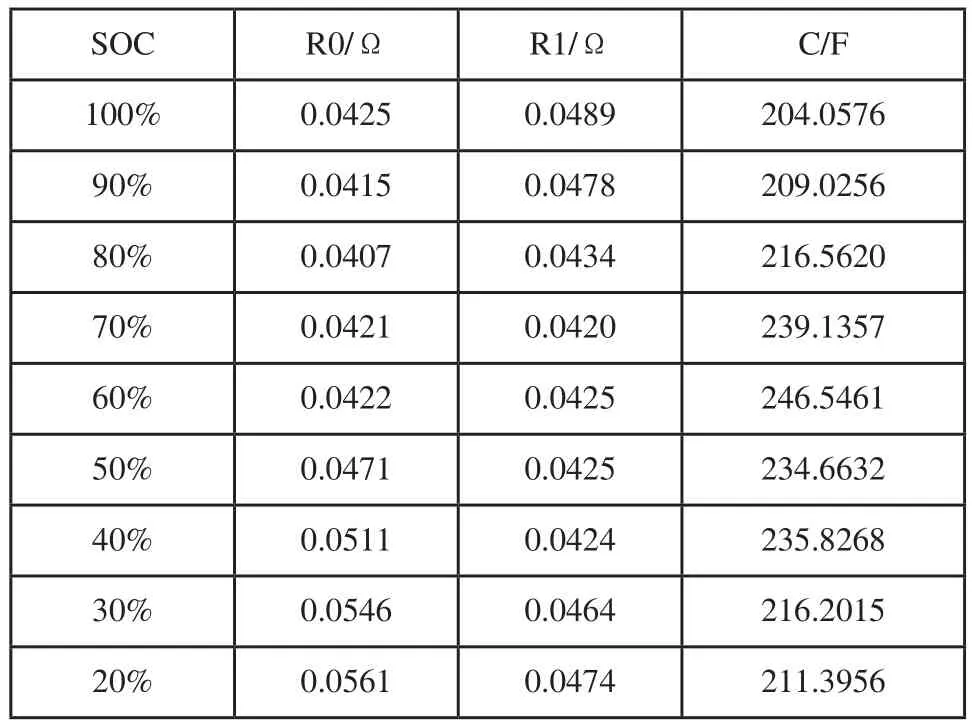
表1 钴酸锂电池Thevenin模型参数与SOC关系表
对各参数关于SOC进行7阶多项式拟合,得到:

2.3 EKF估算小型无人机锂电池SOC实验
通过0.5C恒流放电,联合式(1)、式(2)、式(6)和式(7)~式(10),对本文提出的EKF估算小型无人机锂电池SOC算法进行了验证。处理效果如图4所示。
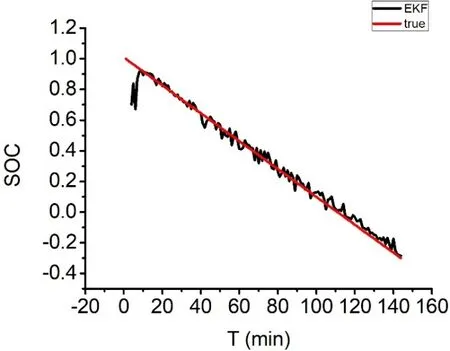
图4 EKF估算钴酸锂电池SOC
图4中,红色曲线是真实SOC,黑色曲线是扩展卡尔曼估计的SOC曲线。

图5 EKF估算钴酸锂锂电SOC误差曲线
误差分析结果如图5所示。图5中黑色曲线是SOC的扩展卡尔曼估算值和真实值的差。发现SOC估算低于4%,在误差允许范围之内。
3 结束语
本文针对小型无人机动力锂电池组SOC在线估计问题,将锂电池组进行Thevenin模型等效,提出了一种基于卡尔曼滤波算法的估算方法。用串联7节4Ah钴酸锂电池组来模仿小型无人机锂电池组进行实验验证。实验结果表明,本文提出的方法对小型无人机锂电池SOC估算误差低于4%,在允许范围内,可以满足小型无人机锂电池组SOC在线估算的要求。
