基于柔性神经网络模糊PID的永磁同步电机调速研究

苏德淳，王仲根

（安徽理工大学 电气与信息工程学院，淮南 232001）

0 引言

永磁同步电机（PMSM）有着体积小、结构简单、效率高、易于维护等优点[1]，广泛应用于驱动系统中，对其控制方法的研究具有重要意义。

PMSM控制系统是一个典型的强耦合、非线性、多变量的复杂时变系统。传统PID控制过分依赖控制对象模型参数，鲁棒性较差。在系统受到内部参数的变化及外扰动时，将难以满足复杂工况的应用场景。文献[2～4]在此基础上引入模糊控制算法对参数进行动态调整，使PID控制器获得更好的控制效果。文献[5]将神经网络引入永磁同步电机PI控制中，提高了控制系统的响应速度，同时减小电机振荡幅度，使其具有较好的鲁棒性。文献[6,7]将神经网络应用于机械人、机械臂的控制中，在相同的期望轨迹条件下，神经网络算法具有更好的跟踪性能。文献[8]表明自适应RBF模糊神经网络控制能快速抑制柔性铰接梁弯曲振动。文献[9]将柔性神经网络用于电机磁轴承径向力的控制系统中，改进了突加负载情况下悬浮开关磁阻电机轴承的径向位移控制系统，明显缩短了转子位置跟踪的动态调节时间。文献[10]为削弱开关磁阻电机（SRM）运行时的转矩脉动，在其直接瞬时转矩控制系统中引入柔性神经网络，验证了低速运行时，柔性神经网络算法对SRM具有良好的控制效果。

本文提出了基于柔性神经网络模糊PID的永磁同步电机控制系统，将模糊PID控制应用在速度控制器中，在保持原有特点的同时结合了柔性神经网络收敛性更稳定与收敛速度更快的优点，并据此对模糊PID的输出变量进行优化。通过MATLAB/Simulink对三种控制算法的电机控制系统进行建模与仿真，验证了采用柔性神经网络模糊PID的PMSM系统响应快、控制精度高、鲁棒性及抗扰动能力强, 提高了对PMSM的控制精度。

1 永磁同步电机数学模型

在d-q坐标系下构建永磁同步电机数学模型，作出如下假设：线性的电机磁路，忽略磁路饱和、涡流与磁滞的影响；电机空载电动势为正弦波分布，无高次谐波；定子电流为对称的三相正弦电流[11]。基于以上假设，得电机数学模型如下：

磁链方程：

转矩方程：

式中：ud，uq分别为d，q轴电压；id，iq分别为d，q轴电流；Ld，Lq分别为d，q轴电感；Rs为定子电阻；ϕf为永磁体的励磁磁链；ϕd，ϕq分别为d，q轴磁链分量；Te为电磁转矩；p为极对数。

2 永磁同步电机柔性神经网络模糊PID控制系统

2.1 柔性神经网络

神经网络算法属于局部逼近法，有着良好的逼近非线性映射的能力。若有足够多的隐含层和隐含层节点，则其可逼近任意的非线性映射[12,13]。

柔性神经网络（FNN）是一种单向传播的多层前向网络，具有传统神经网络（如BP神经网络）结构与权值调整算法，其映射函数参数可调，增加了系统的灵活性[14]。

柔性神经网络隐含层映射函数选取双极柔性S函数：

对式中参数x和a求偏微分：

网络输出层节点的激励函数取单极柔性函数：

对式中参数x和b求偏微分：

FNN算法应用了梯度下降法调整连接权值，同时也在调整柔性函数的参数，输出层调整算法为：

式中：vjl为网络隐含层第j个节点和输出层第l个节点之间的权值，bl为网络输出层第j个节点和输出层第l个节点之间的激励函数。

设误差反馈学习方法的性能指标函数为：

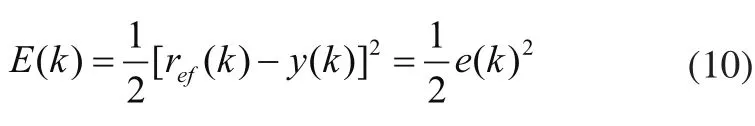
式中：ref(k)为参考转矩信号；y(k)为电机输出的瞬时转矩信号。

为克服局部极小值问题，加快算法收敛，采用带动量项的梯度法。α为动量因子，η表示网络学习率。

隐含层调整算法为：

式中：wij为网络隐含层第i个节点和输入层第j个节点之间的权值，aj为网络隐含层第i个节点和输出层第j个节点之间的激励函数。

本文的柔性神经网络采用4-6-3的结构，如图1所示。

图1 柔性神经网络结构图

神经网络控制器通过以上算法自适应改变联接权值和映射的参数，从而调节输出层神经元，即PID的3个控制参数kp，ki，kd。

2.2 模糊PID控制器设计

二维模糊控制器相当于一个参数可变的PD控制器，本身没有积分环节，因此会存在稳态误差[15]。为消除稳态误差，经积分环节和模糊控制器并联，将其视作参数可变的PID控制器。再与原有的电机直接转矩调速系统的PI控制并联，对其参数进行修正，得到合适的参数，模糊控制结构如图2所示。

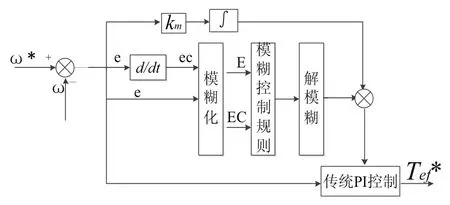
图2 模糊控制框图

模糊控制规则表征了模糊控制输入量和模糊控制量之间的关系。本文所采用的模糊控制规则，根据专家经验建立如表1、表2所示。

表1 KP模糊控制规则

表2 KD模糊控制规则

将柔性神经网络PID与模糊PID控制结合，建立柔性神经网络模糊PID的控制算法，可以改善单个算法在控制非线性系统中的不足。如图3所示的控制系统采用双闭环控制，系统的外环为速度环，通过模糊PID控制器对速度进行调节；内环为转矩环，柔性神经网络PID实现了对转矩的控制。

图3 控制系统框图

3 仿真验证

3.1 仿真模型

通过MATLAB/Simulink建立了如图4所示的仿真模型。仿真参数如下：极对数p=2，定子电阻Rs=2.875Ω，磁链ψf=0.175Wb，定子d轴电感Ld=0.0085H，q轴电感Lq=0.0085H，转动惯量J=0.0008kg·m。

3.2 仿真结果分析

设给定转速为1500r/min，仿真时间为0.1s，为使转速降显示明显，在0.03s时，突加较大的负载即TL=20N。在相同条件下，对本文所述的模糊PID控制、柔性神经网络PID控制及柔性神经网络模糊PID控制对永磁同步电机控制系统进行仿真，并比较结果。柔性神经网络模糊PID控制、模糊PID控制、柔性神经网络PID控制的电机转速如图5所示。

在电机的启动过程中，模糊PID控制的电机虽然转速上升较快，但是其转速不达速且到达稳定转速的时间较长。柔性神经网络PID控制与柔性神经网络模糊PID控制的电机在启动阶段中转速上升速度相同，但柔性神经网络模糊PID能到达的稳定转速较柔性神经网络PID高且能更迅速的稳定下来。

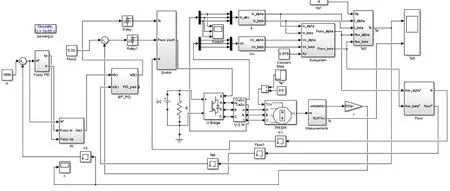
图4 仿真模型

图5 电机启动过程

在突加负载后，如图6～图8所示，模糊PID控制的电机转速下降40r/min，柔性神经网络PID控制的电机转速下降为50r/min，在模糊PID控制下的转速降较低但柔性神经网络PID控制在降速后的转速较模糊PID更稳定，柔性神经网络模糊PID控制的转速只下降了30r/min同时电机降速后的转速稳定性较模糊PID控制有了较大的提升。

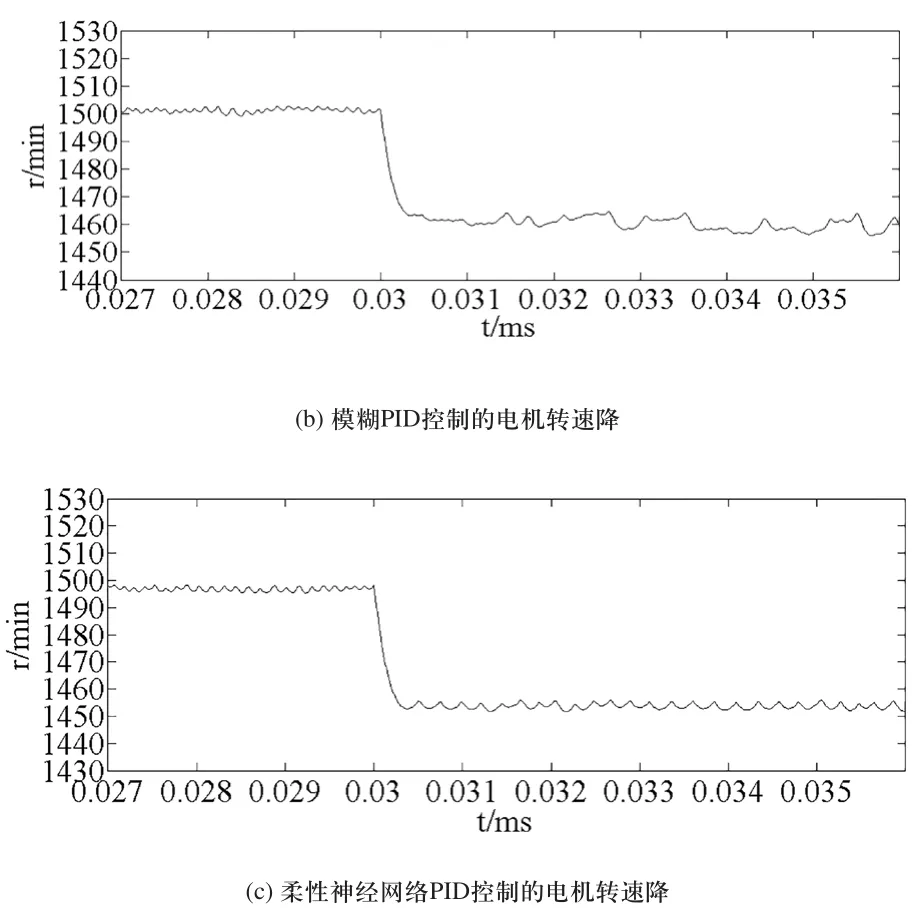
图6 三种控制算法电机转速降比较

突加负载后，柔性神经网络控制下的电机转速下降的较模糊PID控制更多，恢复稳定转速所需时间较长。而柔性神经网络模糊PID控制下的电机转速降较小，且恢复到的稳定转速较高，具有较好的鲁棒性。三种控制算法电机转速比较如表3所示。

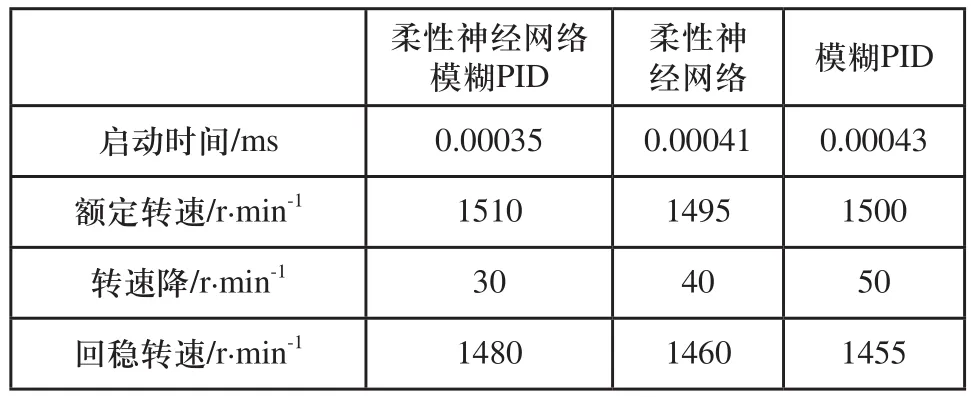
表3 三种控制算法电机转速比较

3.3 转速变化仿真分析

设置电机转速为800r/min，在0.02秒设置电机转速跳变为1500r/min，从图7仿真曲线看出，柔性神经网络模糊PID控制在跳变过程中能更快的到达跳变后的转速。

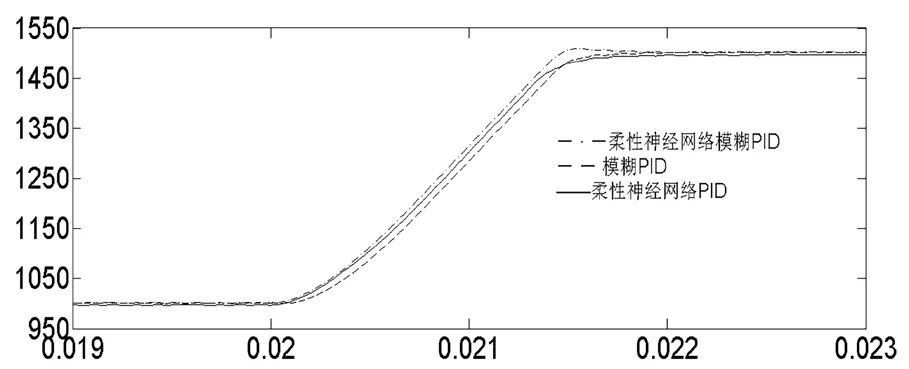
图7 三种控制算法电机转速跳变比较

综上所述，柔性神经网络模糊PID控制与模糊PID、柔性神经网络控制相比较，具有响应速度快、自适应能力强和鲁棒性较好等优点，性能优于模糊PID与柔性神经网络控制。故将柔性神经网络模糊PID控制应用于PMSM控制系统，可得到良好的控制效果。

4 结论

为提高永磁同步电机控制系统的动态性能，本文基于柔性神经网络模糊PID控制对PMSM转速进行调节。柔性神经网络模糊PID控制是在模糊PID控制输出变量的基础上引入柔性神经网络对输出变量进行进一步的修正。

通过MATLAB/Simulink建立其模型，并进行了仿真，仿真结果表明：与模糊PID、柔性神经网络PID控制的电机调速系统相比，应用了柔性神经网络模糊PID算法的PMSM调速系统，可提高电机启动的响应速度，减小启动过程中的振荡时间与幅度，自适应能力和抗干扰能力显著增强，验证了系统具有良好的鲁棒性，电机动态性能得到明显提高。