基于SVD算法的车前影像轨迹提取方法研究

李耀南，周 星，夏修浩

（宁夏大学 机械工程学院，银川 750021）

0 引言

目前，汽车普遍安装倒车影像系统，车前影像系统尚未大面积运用。倒车轨迹的确定是通过计算汽车的运动学方程，求解其运动轨迹方程，根据相对应的运动学模型，对摄像头采集到的数据作处理变换，最终得到可整合在显示屏上的倒车轨迹。文献[1]基于最小二乘法的曲线拟合理论，实现了对倒车轨迹的预测，但是由于其采样点数少，对标定轨迹的有效信息利用也就越少，拟合的轨迹方程的精确度低，且其运行速度较低。文献[2]利用摄像机标定理论，推导出实时倒车轨迹方程算法，通过读取倒车运动车辆方向盘的旋转角度值，可将在世界坐标系下推导的倒车轨迹算法经过摄像机坐标系、成像坐标系和图像坐标系的坐标变换得到倒车预测轨迹，但是在摄像机标定算法理论上需要一个纯二维标定板，而标定纸的取材不同往往会带来误差，而坐标之间的多次变换，运算速度低。文献[3]提出的实时预测倒车轨迹线的计算是通过将CAN总线上的角度传感器的实时信息作为输入，用实时倒车轨迹算法计算出来，这种计算的运算速度较慢。文献[4]提出了一种在特征点匹配的基础上，根据测距原理对特征点进行了深度信息恢复，完成测距目的，根据车辆运动模型，推导出倒车运动轨迹方程，并且轨迹方程高度参数化，方便了平台的迁移。文献[5]提出一种嵌入式汽车鸟瞰全景图拼接算法，可获得近距离道路环境的图像，更好的消除了盲区，提高行驶的安全性，但是由于其价格昂贵，普通汽车消费者无法承担。

受以上研究启发，本文提出了一种基于SVD（Singular Value Decomposition）算法的车前影像轨迹提取方法。轨迹线由动态辅助线和静态辅助线构成，其中动态辅助线与车辆行车轨迹保持一致，辅助司机判断车辆在道路中的行驶情况。静态辅助线为安全预警线，它反映车辆在道路中的位置，反馈给司机直观的图像显示，避免车辆剐蹭并减少在狭窄路况行驶时司机的误判几率，通过仿真实验及误差分析，基于SVD算法对车前影像轨迹的提取可靠性较高，效果良好。

1 车前影像轨迹系统的提取方法

按照阿克曼转向定律[7]，得到车前影像原始图像坐标点，通过SVD（Singular Value Decomposition）算法求出透视变化矩阵，将运动轨迹经透视变化后得到车前影像轨迹的采样点。根据得到的采样点，绘制静态和动态辅助线。对陀螺仪转向角进行设置，使动态辅助线能够较为准确的与陀螺仪采集的数据做出相应的轨迹变化，进而预测车辆行驶时的运动轨迹。微处理器把摄像头实时传输的视频经过处理后，将静态辅助线和动态辅助线与摄像头实时视频叠加后在人机界面中呈现。具体方法设计如图1所示。

1.1 透视变换原理

透视变换（Perspective Transformation）是将一个图像经过投影变换后，得到一个新的视平面。透视矩阵的一般表达形式[8]如式(1)所示。

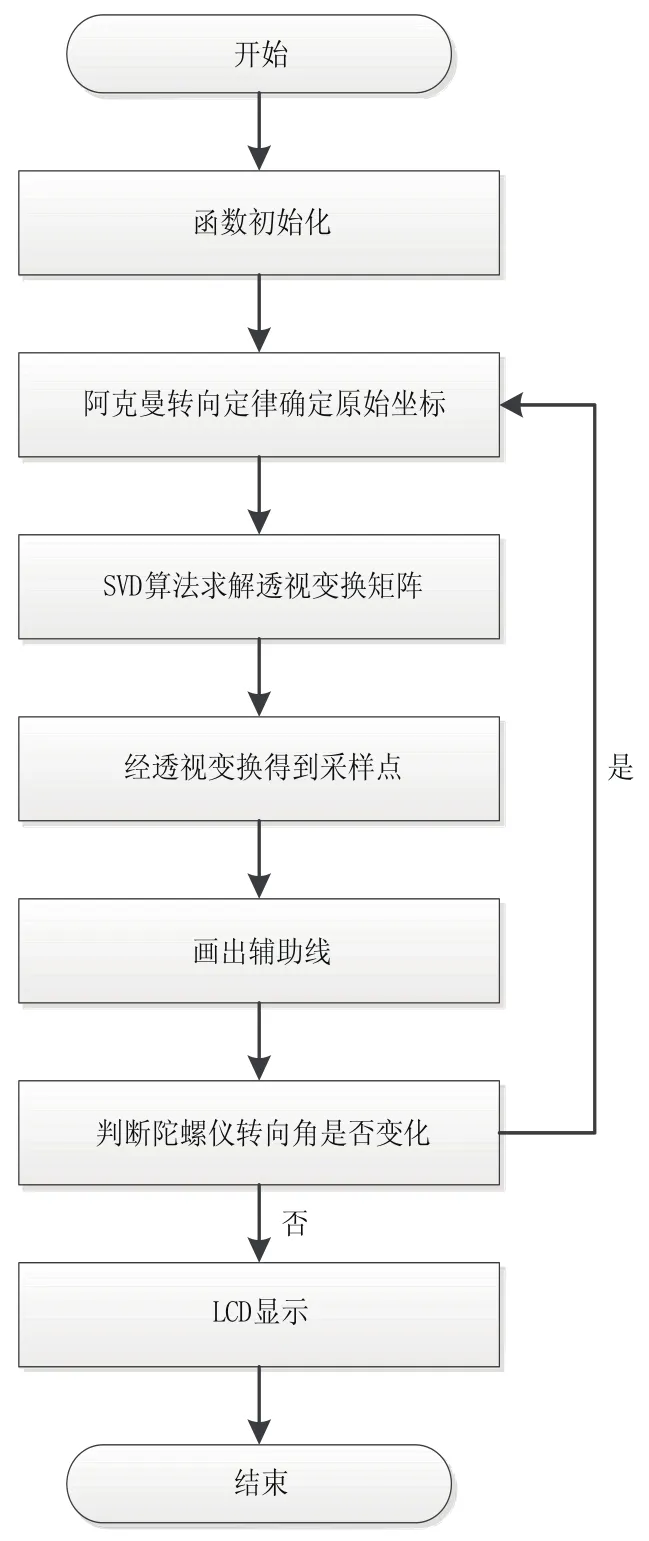
图1 车前影像轨迹提取方法

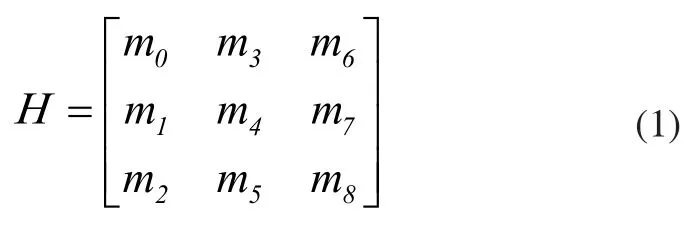
将该透视变换矩阵进行处理后得到透视变换矩阵如下：

A2= [m′2m′5]表示图像的平移，A3=[m′6m′7]T表示对图像进行透视变换。

根据该透视变换的原理运用如下公式对运动轨迹点进行透视变换：

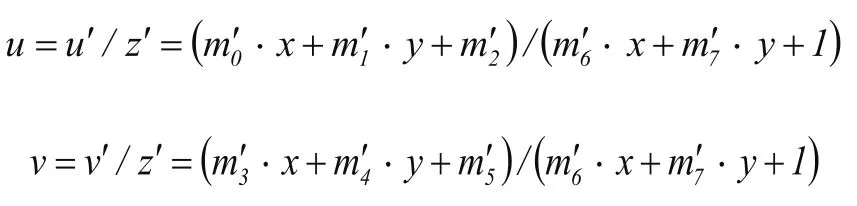
即：

其中为(u′，v′，z′)齐次坐标[9]，原始图像坐标为(x，y)，其齐次坐标为(x，y，1)。变换后图像的图像坐标为(u,v)，[m′6，m′7]T表示透视变换矩阵的透视参数[10]，m′0-m′5为该透视变换矩阵的畸变参数[11]。这里所述的原始图像坐标指的是经过阿克曼转向定律得到的车前影像运动轨迹点，而变换后的图像坐标即为所求的车前影像轨迹采样点。

1.2 SVD算法原理

SVD（奇异值分解）算法的物理意义是：能将任何形式的矩阵用几个子矩阵相乘表示，而这几个子矩阵皆比原矩阵简单，能起到降低维数的作用，其定义[12]如下：

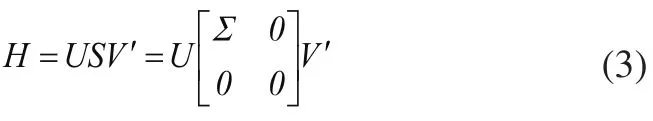
其中Σ是非负对角矩阵，且∑=diag(σ1，σ2，…，σn)，σ1≥σ2≥…≥σn≥0，是S的非零奇异值。

通过SVD算法求解对应的透视变换矩阵，其在本文中具体方法如图2所示。

步骤1：任意构建出一个透视变换矩阵作为基本变换。

步骤2：判断所构建出的矩阵是否满足特定功能，如构建出的矩阵能否实现图形变换的功能，即平移、旋转、比例变换，以及实现透视投影变换等。主要是判断独立透视参数的数量，多于或者少于应有的数量，会使绘制的辅助线杂乱无章或者缩成一个点，违背透视变换矩阵的原理，应该重新构建。

步骤3：SVD算法求解透视变换矩阵，具体的算法如下：

SVD 算法步骤：

1）首先定义一个m×n实矩阵，U为m×m的左奇异矩阵，V为n×n的右奇异矩阵，S奇异值向量。并规定奇异值在S矩阵的对角线上，其他值为0。

图2 SVD算法流程图

2）对该实矩阵进行奇异值分解。取n个奇异值，并对该n个奇异值分别进行判断，若σn＜1.0E-9d将该奇异值舍弃。

3）输出U、S、V矩阵。

4）判断返回值，其大于0则分解成功。若其返回值小于0，则重复上述步骤。

步骤4：判断求出的A3中的参数是否小于零。透视参数小于零，则能够增强其透视感，使绘制的辅助线具有层次感。

步骤5：得到透视变换矩阵。

步骤6：结束。

1.3 采样点的求解

依据阿克曼转向定律[7]，确定车前影像运动轨迹原始坐标点，本文构建全局坐标系Xi0Yi和车辆局部坐标系XtMbYt，如图3所示。

图3 车辆局部坐标系与全局坐标系

Mf为前轴的中点坐标，Mb为局部坐标系原点，θ为局部和全局参考系之间的角度差，0′为瞬时中心点，汽车转向时绕着该点做圆周滚动。且前内轮与前外轮转角应满足定义[13]：ctgβ-ctgɑ=K/L式中β表示汽车前外轮转角，ɑ表示汽车前内轮转角，K表示两主销中心距，L表示轴距。在进行轨迹点的采取时，本文将这些参数分别进行初始化设置：内轮最大转角ɑ=42°，因为一般最大偏转角大约在(34°-42°)[14]，前外轮转角β=40°，要求其转角最大误差为2°，K/L=0.43，本文以K=1420mm，L=3300mm的汽车为例。全局坐标点与局部坐标点之间应满足关系式[15]：

通过Matlab R2013a处理后，其采集到的轨迹原始坐标如表1所示。

本文对SVD算法中参数进行了初始化设置，即m=n=3，表示为一个3×3的实矩阵。则奇异值个数n=3。

调用Matlab R2013a中的SVD算法指令求出U、S、V矩阵分别为：

根据SVD算法原理，即H=USV′，V′是指V的逆矩阵，得到透视变换矩阵H：

将该透视矩阵进行变换后可得：

其中该透视变换矩阵中的透视参数（-0.3288，-0.0365）小于0，该透视变换矩阵能满足要求。

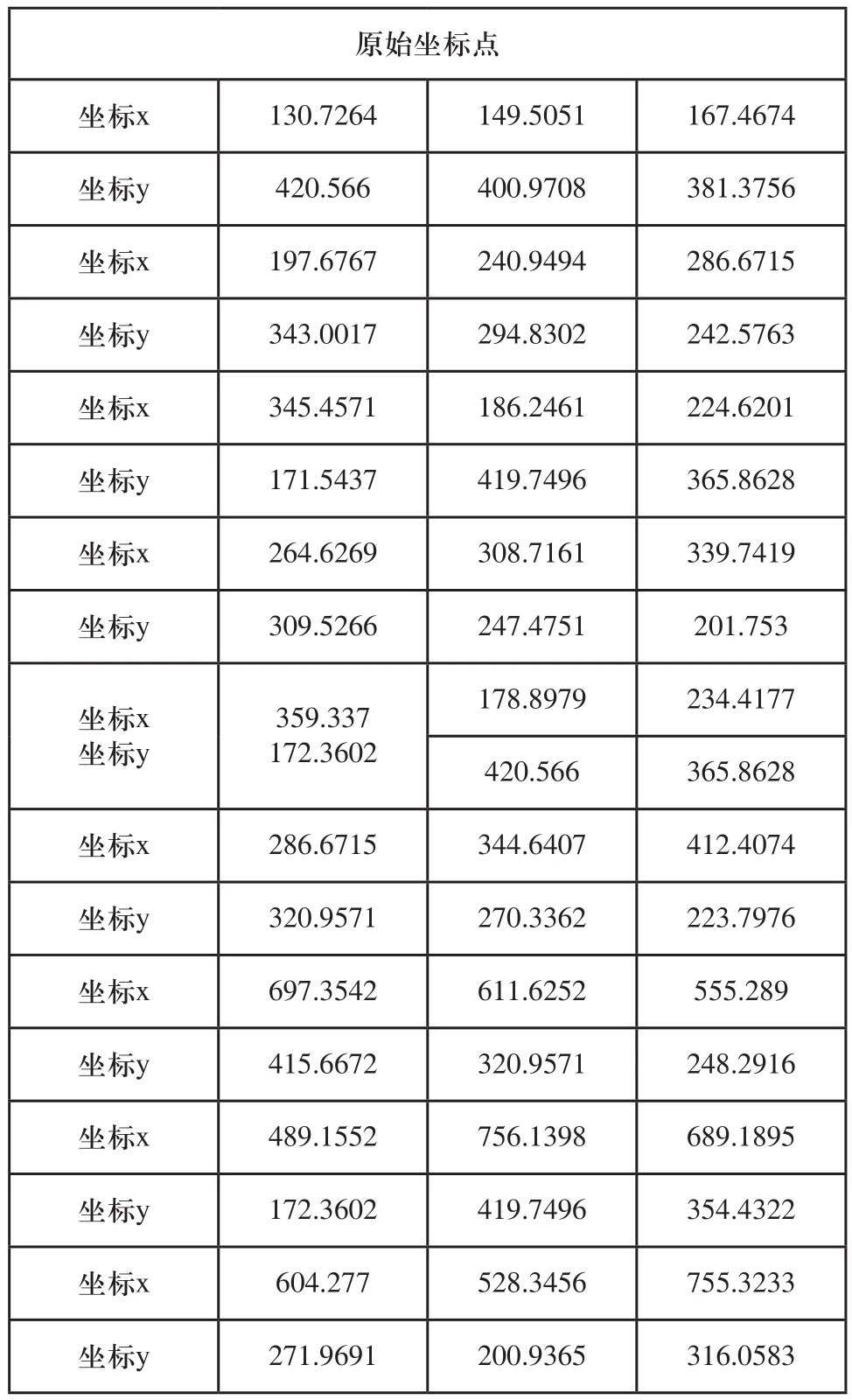
表1 原始坐标点

分别把原始点的坐标x和坐标y生成一组9×3的矩阵，用该坐标矩阵乘以透视变换矩阵H，即可得一组采样点坐标，如表2所示。

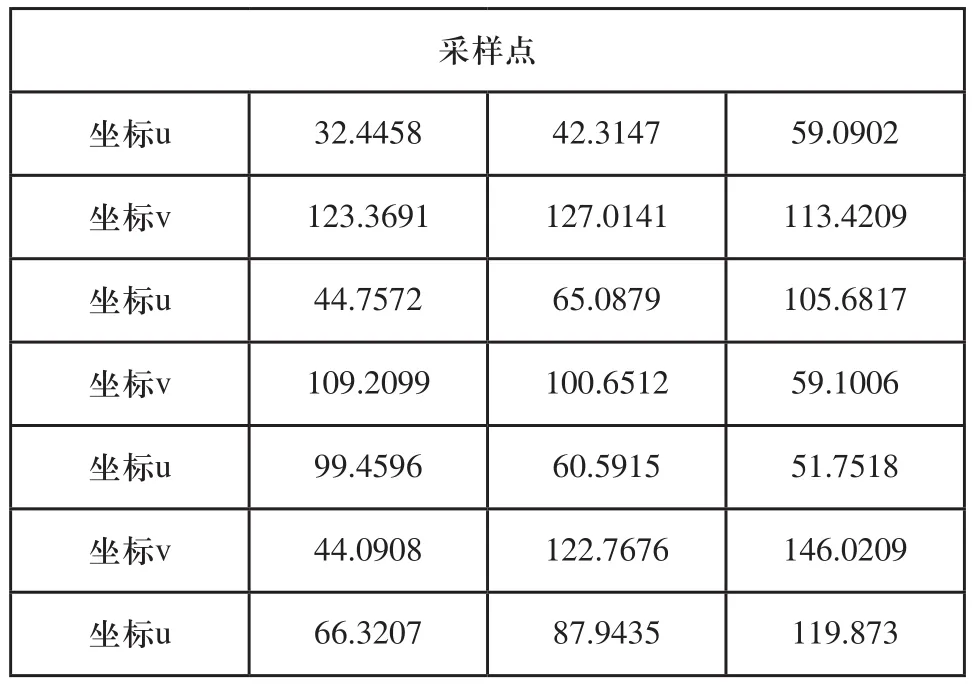
表2 采样点坐标

续（表2）

根据透视变换求解得到的采样点绘制车前影像轨迹，如图4所示，用实线绘制静态辅助直线，虚线绘制动态轨迹线。

图4 车前影像轨迹线

图中的1号线为安全线，它向车辆两侧各延伸一定的相同的距离，当前方的障碍物落在此线以外，车辆处于绝对安全的行驶状态，车辆可以顺利行驶。2号线是根据车辆自身的宽度所绘制的静态辅助线，当障碍物出现在红线之内，车辆不能自由通过前方的道路，此时司机应该做出相应的调整。3号线是动态辅助线，它与车轮的转向角保持一致，能较准确的预测车辆行驶轨迹。通过该车前辅助线进行辅助判断，有助于司机更好的掌握车辆在复杂路况下的行车位置，降低狭窄路况对车辆磨损剐蹭的发生。

基于SVD算法对车前影像轨迹的提取，使得绘制出的静态辅助线较为平滑，动态辅助线也较为精确的反应出车辆的偏转角度，同时能对车辆偏转轨迹进行较精准的预测，抗干扰能力强。

2 实验设计

根据车前辅助线的生成原理，若使动态辅助线能够实时预测车前影像的运动轨迹，需要对陀螺仪转向角进行设置，将其集成到影像图中，再经过图像的实时处理，便可准确的将车前辅助线显示在显示屏。实时处理的主要内容是处理摄像头采集到的图像，实时传输到人机界面上，该过程包括了对图像的校正处理，对静态、动态辅助线的集成。

为验证系统的可行性，本文制作小车模型，选择微雪Raspberry Pi 3 Model B树莓派作为微处理器，开发板运算能力满足画线要求。摄像头型号为Raspberry Pi Camera OV5647；显示器型号为微雪5寸HDMI LCD显示屏：角度传感器型号L3G4200D：其最终呈现在显示屏上的效果如图5所示。

图5 实际效果图

实验结果：图中在地面上的两条黑线为模拟实际路况所画，动态辅助线能够较为准确的与陀螺仪采集的数据做出相应的轨迹变化，来预测车辆前进的运动轨迹。静态辅助线也更直观的表示出车辆在道路上的行驶位置。

与传统的倒车影像不同，该车前影像能够帮助司机在行驶中对前方路况做出更好的判断。在狭窄路段，该系统可给予司机一个本车车宽是否适合通过前方路况的清晰认识。在转弯路段，动态辅助线可较为准确的预测车辆偏转角度，司机做出相应的调整，降低隐患。

3 结论分析

为检验车前影像轨迹系统的可靠性，本文在PC端进行了仿真模拟，由于在PC端进行仿真时，无天气、能见度、光照、行人、路况等因数的影响，可近似的认为PC端呈现出来的静态与动态辅助线是理想轨迹。通过小车模型上呈现的车前影像轨迹与PC端呈现的理想轨迹进行对比，分析该模拟轨迹的相似率，此相似率是指通过对比模拟轨迹与理想轨迹的相似程度。

由于汽车的前轮最大偏转角因车型而异，一般最大偏转角大约在（34°-42°）之间。通过角度传感器可以快速准确的测出前轮的转向角度[16]。本文选取的转向角度值分别是 0°、8°、-8°、15°、-15°、30°、-30°、40°，规定负号表示方向盘向右偏转。通过Matlab分别将小车模型采集的不同偏转角度下的模拟轨迹与理想轨迹进行轨迹线提取与细化处理，如图6所示，并进行相似度对比。对比结果如表3所示。基于文献[1]中所描述的最小二乘法对轨迹拟合的相似度如图7所示。

图6 误差分析图

图7 两种轨迹提取方式相似度对比图

表3 基于SVD算法的轨迹提取的相似度结果

通过对以上实验数据的对比分析后发现，基于SVD算法对车前影像轨迹的提取比文献[1]基于最小二乘法拟合出的辅助线准确度高，且多项式拟合的轨迹，其运算量随拟合精度增高而增大，而本文的方法则无此弊端。

基于SVD算法提取的模拟轨迹与理想轨迹的相似度结果在0.90～0.92的原因如下：

1）相机拍摄照片时由于拍摄高度不同，拍摄光线的不同都会使得在对照片进行处理的时候带来误差。

2）对照片进行细化处理时，我们只选择了其中一条动态辅助线进行相似度对比处理。

3）在对偏转角进行选取的时候，忽略了小车与地面的摩擦，使得在同一角度下的模拟轨迹与理想轨迹本身就存在了误差。

4 结束语

本文提出的基于SVD算法对车前影像轨迹的提取，能对动态轨迹实现较为精确的预测。相比于最小二乘法拟合的车前影像轨迹，该法绘制的轨迹具有更高的可靠性。以一种更加直观的方式降低司机对车辆能否通过狭窄路况的误判。如何将该系统推广到无人驾驶技术中，是进一步研究的方向。