不可压缩流动的非结构网格自适应方法研究*

姜晓坤 李廷秋

(武汉理工大学交通学院 武汉 430063)

0 引 言

自适应策略设计的基本思想是基于现有数据对数值解做出误差估计，根据得到的误差指示器调整网格单元或基函数阶数.调整网格单元密度的自适应方法被称为h自适应方法，保持了基函数的阶不变，得到代数的收敛阶，具有较快的收敛性. 与弹性连续介质中的有限元方法不同，不可压缩流动的数值计算需要处理压力速度耦合问题. 分裂格式可以避免在计算对流-扩散，流体流动等问题中求解耦合方程.Selim等[1]讨论了基于增量压力修正分裂格式 (incremental pressure correction scheme, IPCS)的自适应有限元法求解不可压缩流动，观察到时间步长与动量方程计算误差呈线性关系，与连续性方程的计算误差呈平方关系. Shen等[2]利用离散微分算子推导了一致分裂格式在流场计算中压力-速度的最优误差估计，但将一致分裂格式应用在自适应方法还未见研究. 不同于IPCS这类基于压力/速度修正的分裂格式，一致分裂格式没有分裂误差，在涡量和压力求解上可完全准确求解. 一致分裂格式具有无条件稳定的特点，较能满足海洋工程复杂流场计算中高精度、高稳定性的要求.

文中基于一致分裂格式，针对物体边界网格密度不足的问题，开发了基于误差指示器的非结构网格自动加密模块，应用在有限元流场求解程序上.讨论了网格加密比率、最大加密迭代次数以及初始网格密度在圆柱绕流问题上的误差分析. 依照不同的受力构建了误差指示器. 最后讨论了方形体绕流计算中不同分裂格式的计算效率与计算精度情况.

1 求解器数值验证

计算误差η由空间离散误差ηh，时间离散误差ηc及数值误差ηk组成.

|η|=|ηh+ηk+ηc|

(1)

文中主要讨论通过加密网格减小空间离散误差ηh的手段提高计算精度，首先验证一致分裂格式的求解器在求解绕流问题上具有一定的数值精度，即在保证了数值精度的条件下，可以将ηk近似为0.

待求解的N-S方程与连续性方程可简要表达为

ut-νΔu+uu+p=0,▽·u=0

(2)

式中:u为速度矢量;ν为粘性系数;p为压力.

基于文献[3]中的DFG 2D-2基准测试验证有限元求解器在非结构化网格下的数值精度. 计算域见图1，来流速度定义为

(3)

式中：y为速度入口处纵向坐标；Re=100.

图1 验证算例的计算域

图2 验证算例t=8 s时刻圆柱附近速度云图与网格划分

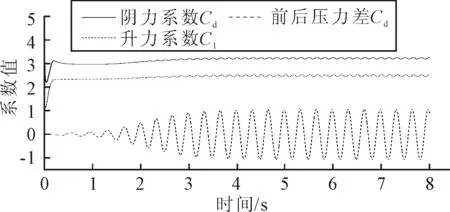
图3 验证算例圆柱受力系数历程曲线

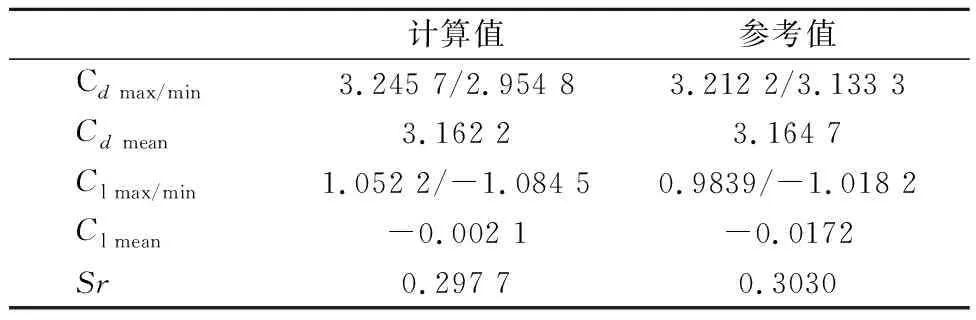
计算值参考值Cd max/min3.245 7/2.954 83.212 2/3.133 3Cd mean3.162 23.164 7Cl max/min1.052 2/-1.084 50.9839/-1.018 2Cl mean-0.002 1-0.0172Sr0.297 70.3030

注：Cvd-阻力系数；Cl-升力系数;max,min,mean-最大值、最小值与平均值.

验证算例表明，基于一致分裂格式的流场求解器有较好的数值精度与稳定性.

2 基于一致分裂格式的自适应方法

2.1 一致分裂格式

一致分裂格式由Guermond等[4]提出，其基本思想是基于空间的连续性推导出压力变分式，并结合不可压缩连续性方程求解压力的近似值，然后对压力进行插值并带入动量方程更新速度. 一致分裂格式的流程如下.

(4)

步骤2将压力近似值带入动量方程的变分形式求解当前速度.

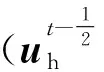
(5)

式中：v为速度场至希尔伯特空间的投影向量；σ为科氏应力张量；ε为速度的对称梯度，定义为

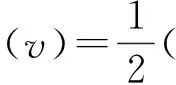
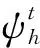
[,,q]/Δt

(6)

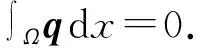
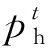
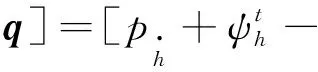
(7)

与速度/压力修正算法相比，一致分裂格式在压力上没有分裂误差. 一致分裂格式在压力收敛上速度更快，可以达到二阶的收敛速度，而增量压力修正方法压力收敛速度仅为一阶。

2.2 误差指示器与自适应算法

误差先验估计是一个对偶问题，相关的数学推导可参考文献[5]，本文仅对误差表达与指示器做一般性阐述.

首先，根据伴随方程的解φ得到误差目标函数M为

M(e)=r(e,φ)=r(u,φ)-r(U,φ)=-r(U,φ)

(8)

式中:误差e可表示为e=u-U，u为对偶问题中的测试函数(test function)解，U为变分方程近似解. 将目标函数表达为空间离散形式：

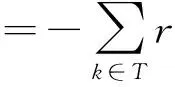
(9)

式中：k为每次迭代步中需要加密的网格比例. 需要加密的网格单元误差指示器为εk=|r(U,φ)k|. 为了防止自适应全局加密时指示器r(U,φ)=0而局部的误差指示器不为0的情况，将误差指示器修改为

εk=|[r(U,φ),Z-πhZ]k|

(10)

式中：πh为矢量速度场与压力在半离散空间上的插值.

自适应算法流程为：

步骤1选择初始的网格作为起始猜测值.

步骤2基于一致分裂格式求解t=j时刻的速度与压力.

步骤3利用求解弱对偶问题的残差绝对值与速度/压力之间进行插值，求得每一个单元的误差指示器εk.

步骤4使用Rivara加密方法[6]对网格比例k的网格进行加密，当小于最大迭代次数或不满足收敛准则时，返回步骤3.

在构建误差指示器时，得到插值πh时需要分析耦合方程的误差. 使用一致分裂格式无需讨论分裂误差项，误差指示器εk计算更加简洁.

3 自适应方法数值分析

3.1 圆柱体绕流问题的自适应

根据以上算法，采用与验证算例相同的计算域，在流体完全流入计算域的时刻，开始网格迭代自动加密. 圆柱绕流在迭代的非结构网格自适应示意图见图4.使用全局加密的方法，可以观察到自适应模块在圆柱附近自动加密了网格. 与手工加密网格的结果(见图2)相比，自适应网格具有一定的非对称性，且加密区域集中在圆柱分离点处. 该示意图说明非结构网格自适应模块很好的处理了初始网格过于稀疏的问题，并且在圆柱尾流处加密幅度较小，较能符合区域自适应的要求.

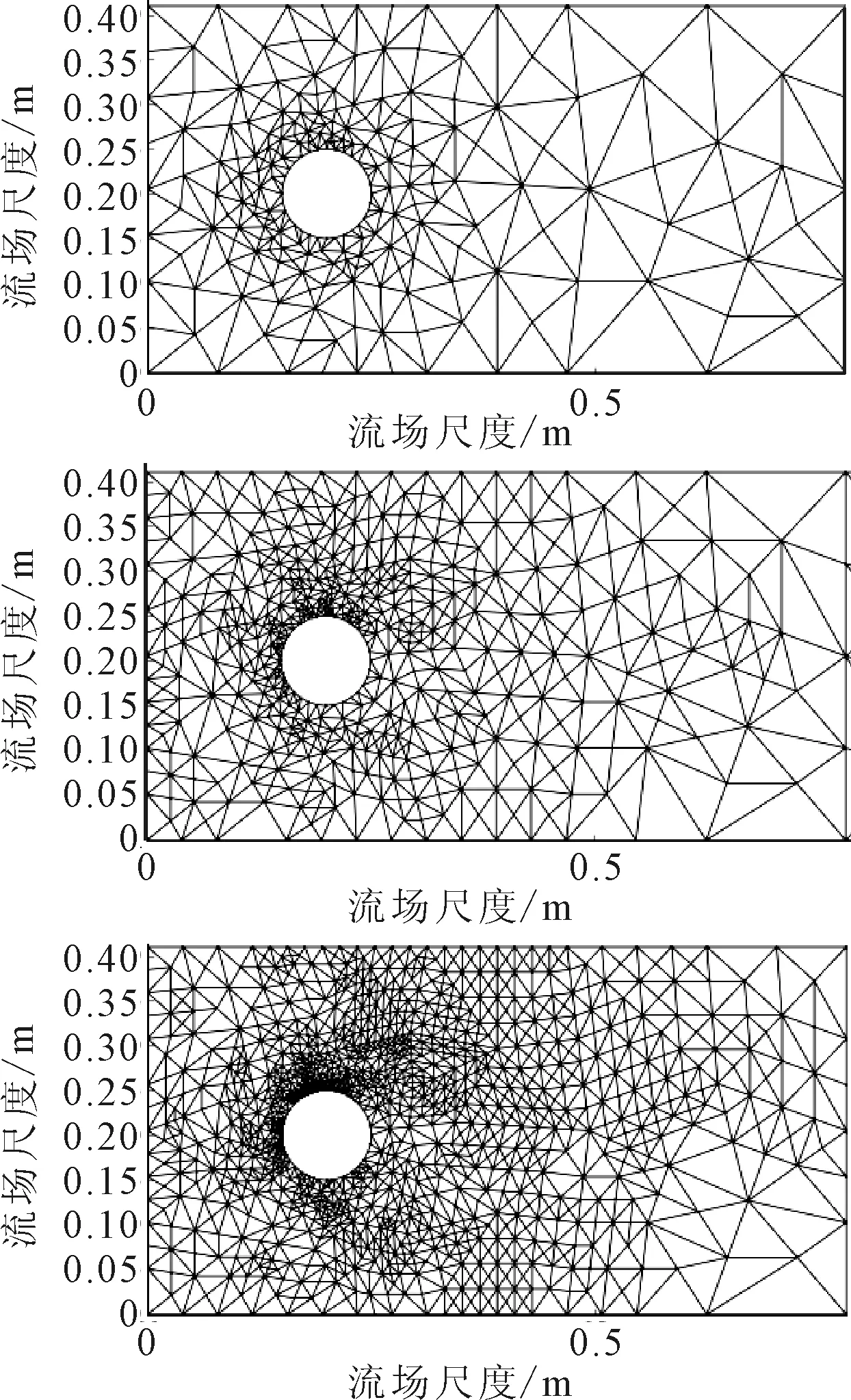
图4 三个加密迭代步下的圆柱绕流网格自适应

在自适应误差估计时，需要误差目标函数，分别定义为

压差阻力(M1):

压差升力(M2):

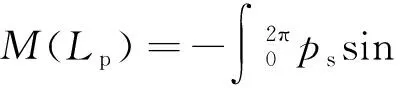
摩擦阻力(M3):

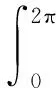
(11)

文献[7]对圆柱后方的尾涡进行了自动加密，但在海洋工程实际应用中，更关心的是圆柱体的受力尤其是升力系数的计算精度，基于圆柱压力构造的目标函数更符合工程实际需求.

三种误差目标函数下网格加密比率k值以及最大迭代次数对计算误差的影响见图5，其中，refined表示初始网格加密后的结果. 可以观察到：①网格加密比率k对计算误差没有显著影响，当最大迭代次数达到一定次数后，计算精度有逐渐收敛的过程；②应用不同受力构造的误差目标函数，其计算误差有较大差异，且摩擦阻力构造的误差函数的网格加密对圆柱绕流数值精度有显著提高.

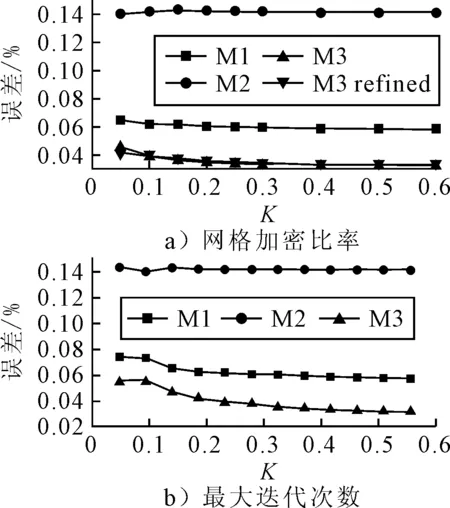
图5 圆柱绕流不同误差目标函数随网格加密比率及最大迭代次数计算精度曲线

3.2 方型体绕流问题的自适应

方形体绕流算例主要讨论尖锐界面下的自适应策略及自适应方法在非对称绕流问题下的计算情况，计算域设置与文献[1]一致.

基于均匀的非结构网格，方型体绕流在五个迭代步下的自适应见图6，可以观察到尖锐点处的网格得到了很好加密，对梯度变化较慢的区域如角落处的网格加密较小，同时自适应模块在方型体顶部后方流速较快的区域也加密了网格，对应的速度云图也得到了一定的光顺.

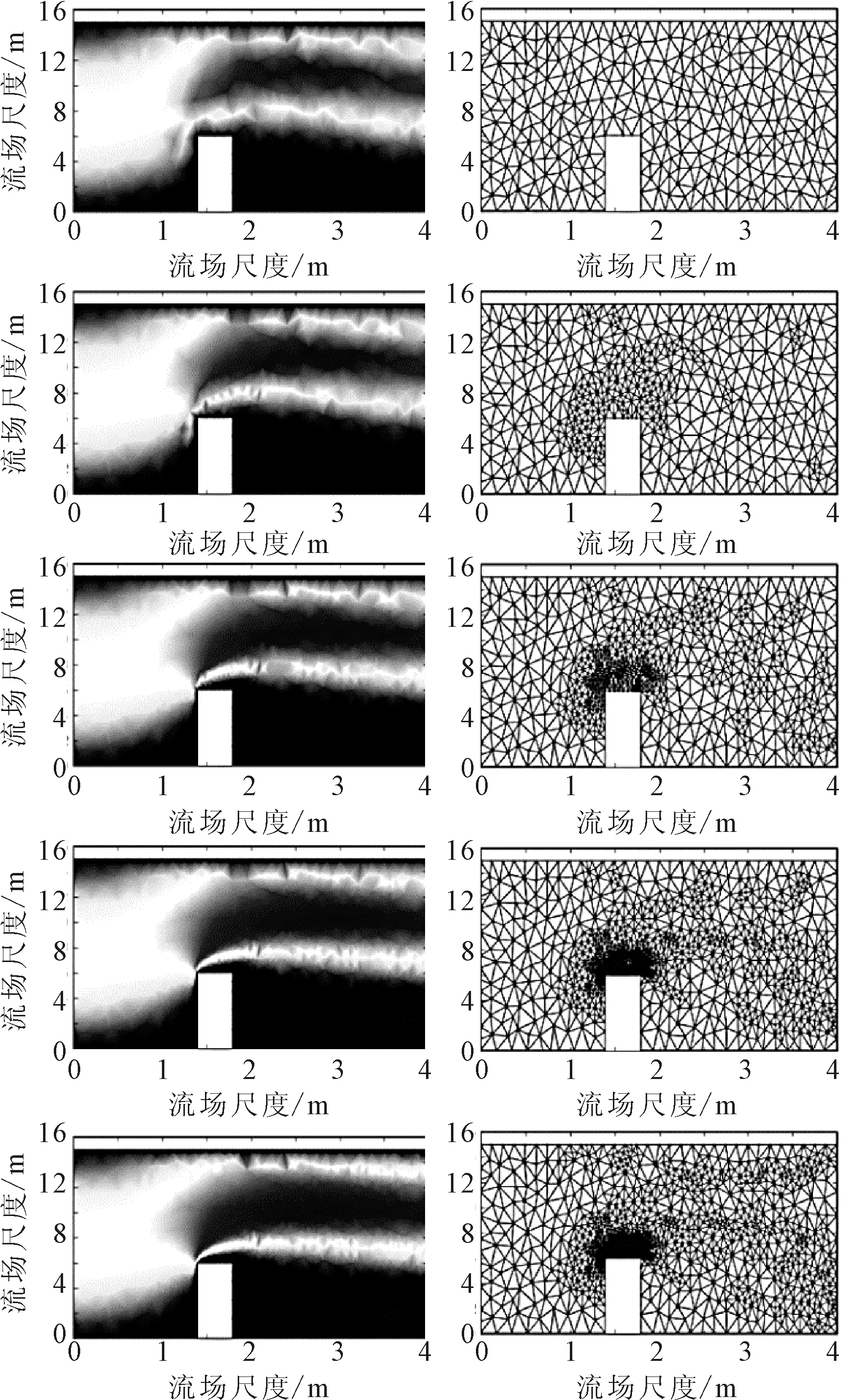
图6 方型体绕流迭代自适应的速度云图与网格变化

不同误差目标函数随网格变化比率k的变化曲线见图7，和图5a)不同，压差升力的计算精度明显高于摩擦阻力和压差阻力，且随着网格加密比率的增大，计算精度反而有减小的情况. 贴壁的方型体绕流与圆柱绕流问题不同在于：流体在迎流面会向上流动，作用于物体一个向上的升力，而将阻力作为误差目标函数并不能反映出这一受力. 圆柱绕流的升力一直在零值处作周期性振荡，网格自适应如果对频率较快的波动流场进行网格调整，计算耗时较长.

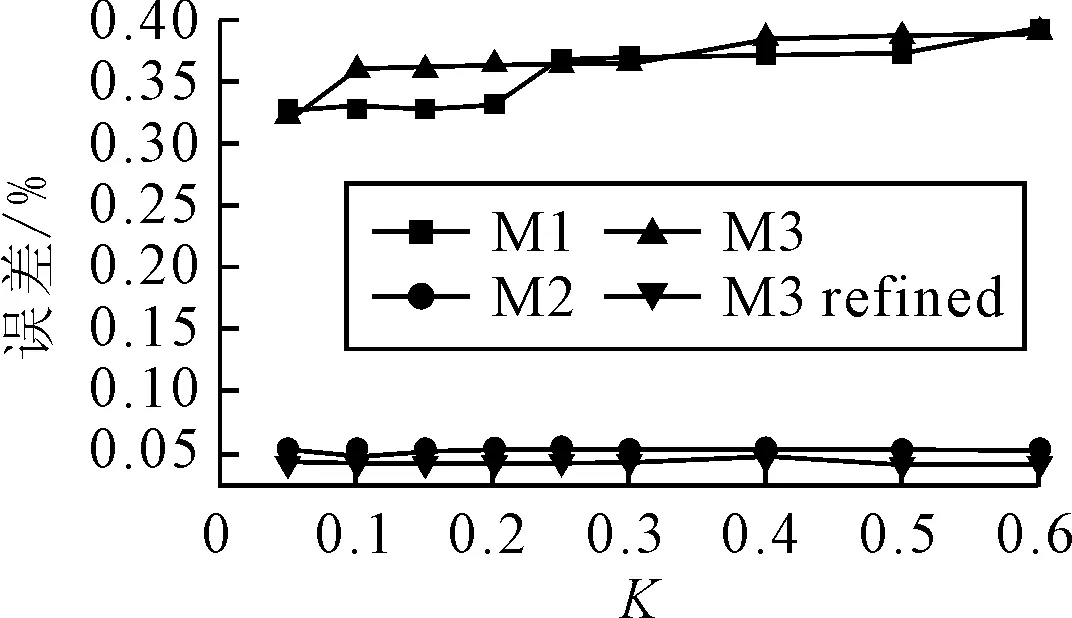
图7 圆柱绕流不同误差目标函数随网格加密比率计算精度曲线

Chorin投影法、增量压力修正，以及一致分裂格式随网格数的增加其计算时间与计算精度曲线见图8.

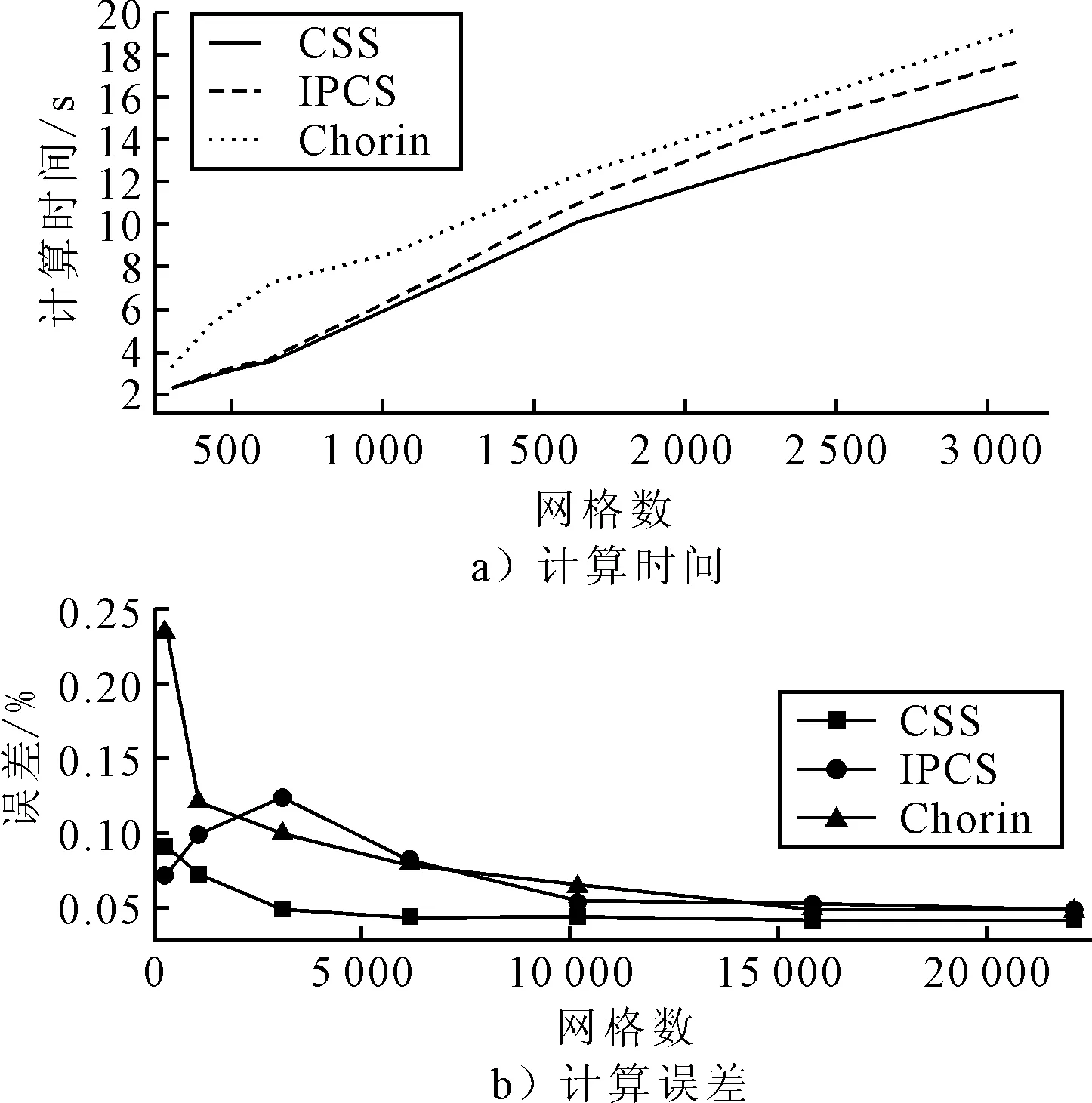
图8 方体绕流不同分裂格式的计算时间及计算误差随网格数变化曲线

由图8可知，一致分裂格式在网格数量增加后相比与经典的分裂格式在计算效率和计算精度上均有一定的优势，但差异不大. 一致分裂格式在网格数量较小时计算精度的波动性较小，随着网格数量的增大，其计算效率有显著的提升.

4 结 束 语

本文主要对绕流问题下非结构网格自适应策略进行了讨论，得出结论有：最大加密迭代次数、初始网格密度以及网格加密比率对计算误差并无显著影响；使用不同的受力特征构造的误差目标函数计算误差影响较大，一致分裂格式与增量压力修正格式与投影法相比，在计算速度上有一定优势.应用到自适应方法时，一致分裂格式无误差项，稳定性较好.

关于自适应算法在计算流体力学的应用值得进一步研究的问题有:①瞬态问题的先验误差估计,即时间步长的自适应调整[9]；②一致分裂格式对周期性边界条件的适应性较差, 而其改进形式或其他现代分裂格式在自适应方法中的应用需要进一步探讨[10]；③运动物体以及多体问题的网格自适应问题，其核心在于网格自动生成的方式，基于笛卡尔网格以及切割网格法的h块自适应方法[11]在这一领域具有良好的研究价值.