递归边缘保持型双目立体匹配算法研究*

帅 然 吕植勇 刘昌伟 赖俊豪

(武汉理工大学国家水运安全工程技术研究中心1) 武汉 430063) (武汉理工大学能源与动力工程学院2) 武汉 430063)

0 引 言

局部立体匹配算法研究的早期出现了一种基于固定大小窗口的局部立体匹配算法(fixed window，FW)，该算法具有比较简单的计算过程[1]，在双目图像立体匹配算法研究的初期占有重要地位.由于双边滤波(bilateral filter，BF)技术很早就应用于图像处理领域，Gao等[2]发现可以将这种技术推广到双目视觉领域后，提出自适应权值双目立体匹配算法(adaptive weight，AW).该算法的计算复杂度比较高，能够获得与先进全局匹配算法相近的匹配精度，但是在实时性方面的表现却不尽人意.

李超[3]提出了一种具有固定时间常数的立体匹配算法，以前经典的双边滤波式局部立体匹配算法在进行匹配时需要用到匹配窗口，因此最后的计算复杂度与窗口的半径的平方成线性关系，而他提出的算法在匹配计算时与窗口大小无关，计算复杂度为一个固定时间常数O(1).在此研究基础上，Zhang等[4]提出了改进型的自适应权值双目立体匹配算法，该算法也具有运行时间为常数的特点，该算法虽处理灰度图像且匹配效率也较高，但与能处理彩色图像的传统自适应权值算法相比，在匹配精度和效率方面还是有差距.He等[5]借助联合积分直方图技术，提出了新的改进型自适应权值立体匹配算法，该算法不仅能够处理多通道的彩色图像而且计算复杂度也具有固定时间常数，更重要的是与以前的算法相比，匹配精度也有较大的提升.

CostFilter算法[6]是当前匹配精度最高的局部立体匹配算法，性能指标接近最为优秀的全局立体匹配算法，进一步推动了局部立体匹配算法的研究工作.因此总的来说近年来的发展趋势和重点仍旧是在局部匹配算法上，主要是追求计算效率的高效化和匹配精度的高质量上，本文后面提到的主要图像处理算法思想也是基于此目的来展开研究与开发的.

1 双目图像处理算法的建模

1.1 递归型信号滤波数学模型

IIR数字低通滤波器是一种很重要的数字滤波器，其具有设计简单、方便实现等特点，在语音信号处理过程中运用得比较广泛.常用的IIR的输入输出差差分方程表达式为

λjF(n-j)

(1)

式中：N为前N个输出时刻；M为当前有M个输入信号，且一般N>M.IIR滤波器系统存在反馈作用，反馈系数为λ，ξ为输入系数，而且该差分方程的实际运算过程中一般通过递归的编程方式来实现，所以该数字低通滤波器也称为递归型数字滤波器.最简单的一阶递归数字信号低通滤波器的差分方程表达式为

ξiI(n-1)+

(2)

1.2 递归型图像滤波数学模型

当把递归信号滤波模型引入到图像滤波领域时，需要做如下处理：首先将输入图像I按照Y轴方向划分为yn条扫描线，其中第yi条扫描线又包括[I(yi,1)，I(yi,2)，I(yi,3)，…，I(yi,n)，…]这些像素点，见图1.

图1 图像序列扫描线示意

将这些像素点序列当作一个时域的输入序列，可以推导出一阶的图像滤波输出为Ox+，具体运算表达式见式(3)～(4)，其中令反馈系数λ<1，且ξ=1-λ.

Ox+=(1-λ)I(n,yi)+λox+(n-1,yi)

(3)

(4)

考虑到图像滤波的特殊性，该点的滤波输出不仅与左边的像素点有关，还应考虑到该点右边像素点对它的影响，因此可将式(4)扩展到图像I的整个宽度W上，最后推导简化后的一维滤波输出的表达式为

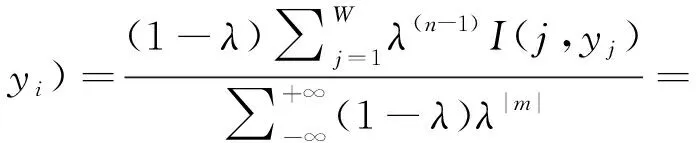
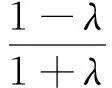
(5)

Ox(n,yi)=I(n,yi)*H1(n)=

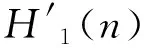
(6)

整理后的最终输出结果表达式为

Ox(n,yi)=(1-λ)Ox(n,yi)+

λOx(n+1,yi)

(7)

进一步延伸到图像I在X轴上的扫描线，同样需要进行Y轴正向、反向的滤波过程.其中第xi条扫描线按时域分割后的序列进行Y轴方向的滤波输出结果的表达式，可以采用上面相似的原理推导出来.同时可以利用二维卷积，将一维滤波核H1扩展成二维滤波核H，具体表达式为

*H1

(8)

由式(8)的表达式进行推导后可以得到整个图像I的二维滤波核的表示式，即H(x,y)=(1-λ)2λ|x|+|y|，最终的图像I的滤波输出O的计算结果为

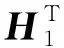
(9)

由式(9)可知，图像I的二维滤波可以分别进行X轴和Y轴双向滤波就可以完成.

1.3 梯度域递归边缘保持图像滤波数学模型

Gastal等[7]提出了域变换(domain transform)的概念，并通过该概念提出了自己的图像滤波模型.他将双边递归滤波算法中的反馈系数λ由一个常数改进为一个变化量，该变化量主要与当前元素和前一个元素的差值ΔI相关的变量λ’，具体表达式为：λ’=λΔI，这样处理后，不仅能对图像进行递归滤波处理后获得比较平滑的效果，同时又能借助新的反馈系数使图像滤波能很好的保持图像的边缘特征.

根据该算法模型，则图像I沿X轴正方向的滤波表达式为

Ox+(n,yi)=(1-λΔIx-)I(n,yi)+

λΔIx-Ox-(n,yi)

(10)

式中：ΔIx-=1+β|I(n,yi)-I(n-1,yi)|；β为差分调节参数，且β=δs/δr，δs为空域方差，δr为值域方差.其他方向上的滤波表达式都可以由类似式(10)的方法推导出来，这里就不赘述.

采用这种方式的递归双边滤波算法，其计算复杂度并不高，因为算法内部主要是乘法和加法运算，所以比较匹配嵌入式处理器有限的运算处理能力，使其计算效率比较高，同时匹配精度也能得到保障.

2 基于REF模型的双目立体匹配代价聚合算法设计

所有的立体匹配算法都需要进行计算代价聚合的过程，而传统的计算代价聚合的方式是通过计算视差窗口内匹配代价的总和或平均值而得到的.从本文第二节所述的REF滤波数学模型可知，输入图像I在经过匹配代价计算后，获得匹配代价矩阵e，对e进行REF滤波时，具体聚合过程可以分为从X轴、Y轴两个方向分别进行滤波处理的过程.式(11)中e矩阵中的一个点P，该点在视差为d的条件下，X轴正方向的滤波处理后得到的聚合代价，进而可以扩展到X轴正负两个方向的聚合代价具体表达式见式(12).而目前主流的局部立体匹配算法在计算代价聚合过程是主要采用边缘保持滤波技术，这样处理可以使不同颜色的像素点都能获得比较小的聚合权值，从而保证代价聚合的效果良好.

Cx+(p,d)=(1-λΔ-p)e(p,d)+

λΔ-(p)Cx-(p,d)

(11)

Cx+(p,d)=(1-λΔ+(p)Cx+(p,d)+

λΔ+pCx+(p+,d)

(12)

式(11),(12)中Δ-(p),Δ+(p)分别为像素点P与正向、反向相邻元素之间的一个差分变量，而p+，p-分别是点P左右两边的相邻元素.以X轴正向为例子，差分量Δ-p=1+β|I1(p)-I1(p-),Δ+(p)=1+β|I1(p)-I1(p+) 其中的β为差分调节参数，它反映的是代价聚合过程的过程随像素梯度变化的程度.

该代价聚合算法一次完整的聚合代价计算过程需要遍历代价矩阵e中的所有元素4次，因此该算法的计算复杂度是一个与输入图像的宽和高息息相关的固定时间常数，即O[4*W*H].

图2为经过REF代价聚合算法处理后的样本图像示意图，实验样本中的绿线为选取的比对图像数据，a行为代价矩阵e的视差图分布图，b行为经过REF滤波处理后的视差分布图，红色部分为其中视差值最小值的点.通过下图图像元素的分析可知：通过匹配代价计算处理后的矩阵e中的视差分布很杂乱，内部存在锯齿，而且过渡不平滑，视差也不连续，边缘特征也保持的不好；而经过REF滤波处理后得到的视差矩阵C中的内部视差过渡连续平滑，变化趋势比较明显，保留的边缘特征效果比较好，因此将REF模型运用到代价聚合的计算过程中是有效的.

图2 REF双目立体代价聚合算法图像处理效果的示意

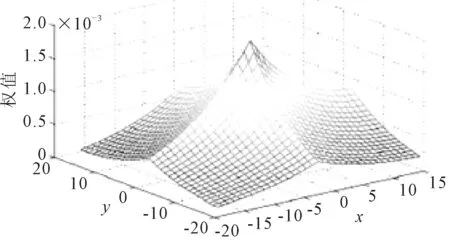
图3 未采用迭代方式的二维滤波权值分布图

图4 三次迭代滤波后滤波权值分布图

由文献[8]可知，N次迭代滤波后的第i次迭代反馈参数为λi，其具体计算公式为

本节后面的实验部分将具体展示REF算法的性能与迭代滤波次数N之间的关系.

3 双目匹配算法的仿真结果分析

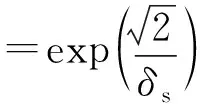
其中δs的取值可以参考经典的AW,FBS等双目算法，取高斯核空域平滑方差经验值δs=30即可，而δr以及N对匹配精度的影响需要做相关仿真实验来确定最优数值.迭代次数N和值域平滑参数δr与误码率的关系曲线图见图5～6.

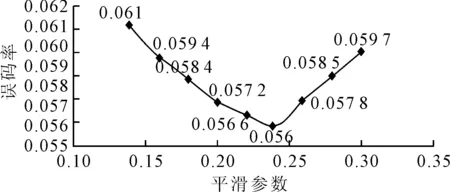
图6 值域平滑参数δr与误码率曲线关系图

由图5可知，经过REF双目立体匹配算法图像处理后获得的误码率随着迭代次数的增加呈现一种震荡收敛的曲线关系，其在N=3时误码率达到最小为0.056，而在N≥5以后误码率逐渐震荡收敛于一个稳定值0.056 4.在实际应用过程中考虑到嵌入式芯片计算资源的有限，不可能选择过高的迭代次数，这会给芯片造成很大的计算负担，而选择迭代次数N=3不仅可以保证比较好的误码率，对计算芯片的运行速度要求没有那么苛刻.不可能选择过高的迭代次数，这会给芯片造成很大的计算负担，而选择迭代次数N=3不仅可以保证比较好的误码率，对计算芯片的运行速度要求没有那么苛刻.

由图6可知，误码率与值域方差δr之间呈现明显的凹曲线关系，在δr=0.24左右时，误码率可以取得最小值0.056，因此，本算法在最后参数的确定环节，影响REF双目匹配算法匹配精度的三个核心参数的取值分别为：迭代次数N=3，空域平滑参数δs=30，值域平滑参数δr=0.24.

经过本文提出的算法处理后，其不仅能够很好的保留图像的边缘特性，方便提取物体的边缘特征用于识别，同时内部还具有均匀的视差分布，方便后期处理时获得连续均匀的3D图像，保证其平滑，观看舒适，立体感强烈.发送误匹配的点主要在物体边缘，这进一步证明了本算法内部可以保证过渡平滑，边缘特征比较明显.

双目匹配算法实时性的仿真结果分析.

本文提出的REF立体匹配算法的计算复杂度主要与输入图像的大小、输入信道的数目以及迭代次数呈线性关系， REF双目立体匹配算法的迭代计算过程中只涉及到加减和乘法运算，没有占用计算资源很多的矩阵运算，因此计算效率较高.输入图像大小为N=h*w时，在D个输入信道下，其计算复杂度为O(4*N*D)，它比目前先进的双边滤波算法(计算复杂度为O(ND2)[9]或者O(Nlg(N)D)[10])更加有效，因此REF匹配算法的运行效率要远高于其他局部匹配算法，在理论分析上具有比较好的实时性能.

在双核AMD2.3 GHz处理器、4 GB运行内存的PC平台上进行本文提出的REF双目立体匹配算法.经过对四个实验样本进行立体匹配过程的运行时间的追踪，具体数据见表1.其中在对实验样本Tsukuba进行一次迭代的时间仅需38 ms，而三次迭代后所需时间也只为108 ms，即使数据量最大的Teddy和Cones实验样本三次迭代的时间也不超过160 ms，对比其他实时性比较好的P-LinearS匹配算法的匹配过程约需要250 ms左右，因此，本文提出的REF双目立体匹配算法具有比较优秀的实时特性.

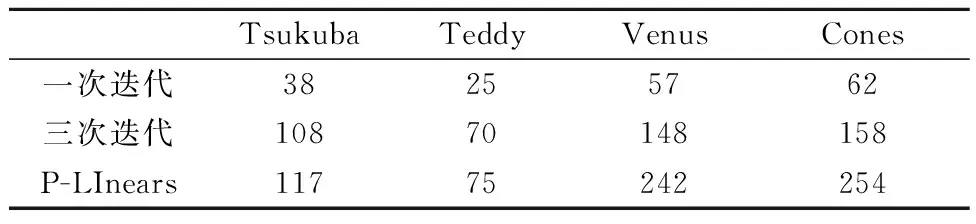
表1 REF立体匹配算法实验样本运行时间数据 ms

4 结 束 语

本文主要开发了一种计算效率高且图像处理精度比较好的图像处理算法，本文根据数字低通滤波器的递归数学模型展开相关研究，将它扩展到图像滤波领域，并以此为核心设计了REF双目立体匹配图像处理算法.REF双目立体匹配算法的图像仿真实验主要是在PC机端实现的，实验的样本主要来自经典的四组立体图像对，仿真实验数据和仿真图像可以得出本文的图像处理算法在匹配精度上领先了几种经典的匹配算法，并与保持领先的局部算法在匹配精度误码率上差距不大，匹配精度平均能够保持在5.6%以下，在图像处理算法的运行时间上优于其他局部立体匹配算法.