基于双向指数平滑的水位数据修复方法*

2018-11-01蒋仲廉刘培豪

武汉理工大学学报（交通科学与工程版） 2018年5期

蒋仲廉刘培豪钟诚余珍李博

(武汉理工大学国家水运安全工程技术研究中心1) 武汉 430063) (武汉理工大学交通学院2) 武汉 430063) (长江航道规划设计研究院3) 武汉 430040) (武汉工程职业技术学院4) 武汉 430415)

0 引言

水位数据在水运工程中具有重要作用.在水位观测中，由于一些仪器故障或人为原因，水位数据的完整性难以得到有效保障[1].在现有的水位数据修复方法中，线性插值方法，如拉格朗日插值法、牛顿插值法、Hermite插值法、三次样条插值法等[2]是较为常用的方法.此外，还有基于潮汐学理论的潮汐调和方法，通过潮汐的正余弦函数分解，对其多阶导进行平滑修正，在感潮河段的潮位分析中得到了广泛应用.在水位时间序列相关关系上，唐岩等通过余水位的空间相关性，对潮高模型进行了精化修复[3].

内河航道由于受地形、天气、汇流及分流等众多因素的影响，其季节性、周期性等特征变化幅度较大，故上述方法在内河水位数据修复、预测中的适用性有待进一步提升.水位数据本质上属于时间序列数据，时间序列是将某种统计指标的数值，按时间先后顺序排列所形成的数列，时间序列分析就是从时间序列数据的分析中寻找其所具有的时序性和规律性，根据时间序列所反映出来的发展过程、方向和趋势，进行类推或延伸，借以预测下一段时间可能达到的水平，其数据本身已经为建模提供了足够的信息量，因而，时序分析方法可在内河水位预测上能取得较好的效果[4-5].

指数平滑法是生产预测中常用的一种时间序列分析预测法，作为趋势外推法的一种，指数平滑法不同于一般的移动平均法(ARIMA).移动平均法中，近期资料对预测结果的影响要大于远期资料，且越近期的资料对结果影响越大[6].而指数平滑法在此基础上，对各期的数据按一定的规律赋予权数，越近期的数据，权重越大；而对于远期的数据，则仅给予逐渐减弱的影响程度，即随着数据的远离，赋予它们逐渐收敛为零的权数.

基于上述分析，本文提出一种基于改进指数平滑法的内河水位预测方法.在修复过程中，对指数平滑法的单向预测过程进行了改进，引入正反双向预测，并对正反向结果进行加权求和，最终实现内河航道水位预测.通过长江中游水位站日均水位数据验证，结果表明本文方法稳定可靠，可有效实现长江等内河干线航道水位数据修复与预测.

1 基于指数平滑法的水位数据修复方法

1.1 指数平滑方法

根据平滑次数不同，指数平滑预测分为一次指数平滑预测、二次指数平滑预测和三次指数平滑预测.它们的基本原理都是预测值是对以前观测值的加权和，且对不同的数据给予不同的权，新数据给较大的权，旧数据给较小的权.基本公式为

St,1=αyt+(1-α)St-1,1

(1)

St,2=αSt,1+(1-α)St-1,2

(2)

St,3=αSt,2+(1-α)St-1,3

(3)

式中：St为t时刻的平滑值；yt为t时刻的实际值；St,1、St,2、St,3分别为一次、二次和三次指数平滑值；α为平滑系数，取值范围[0,1].设次数为3，则三次指数平滑预测的表达式为

yt+m=at+btm+ctm2

(4)

式中：yt+m为第t+m时刻的预测值；at,bt,ct均为t时刻的参数，其值为

at=3St,1-3St,2+St,3

(5)

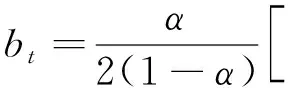
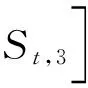
(6)

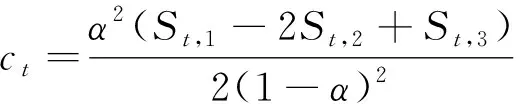
(7)

1.2 双向指数平滑修复方法

将指数平滑法用于缺失数据修复时，通常采用单向的修复方法.本文在单向指数平滑方法基础上，充分利用缺失点前后趋势，对待修复数据进行正反双向预测，并通过正反向预测结果进行加权平均，实现预测结果修正，提高预测精度.双向指数平滑法的预测流程见图1.

图1 双向指数平滑法流程图

2 基于双向指数平滑水位数据修复过程

2.1 平滑系数

指数平滑法的计算中，平滑系数α的取值十分重要，它反映了不同时期的历史数据对指数平滑值的影响.平滑系数α的取值范围在0～1，平滑系数越大，近期实际值对本期平滑值的影响越大.α的取值依赖与时间序列的平稳性，当时间序列呈平稳趋势时，α取值较小，反之，时间序列有较大波动时α取值增大.

时间序列的平稳性检验常用办法有ADF均方根检验方法.取长江安庆段2016年水位数据进行ADF均方根检验，其结果见表1.

表1 均方根检验结果表

在ADF检验结果中，0为非稳定序列，1为稳定序列.其中原始数据检验结果表明原始水位序列并非平稳数据，一阶差分及二阶差分结果均通过ADF检验，表明数据在部分区间段内有抖动情况，但抖动程度并不剧烈.由水位序列数据特性分析，应选取较小的平滑系数[7].分别取平滑系数α=0.2，0.3和0.4进行试算[8]，对安庆段2016年水位数据进行拟合，拟合情况见图2.在长江中下游段，其水位抖动不剧烈的情况下，α取值0.3时有较好的拟合结果.

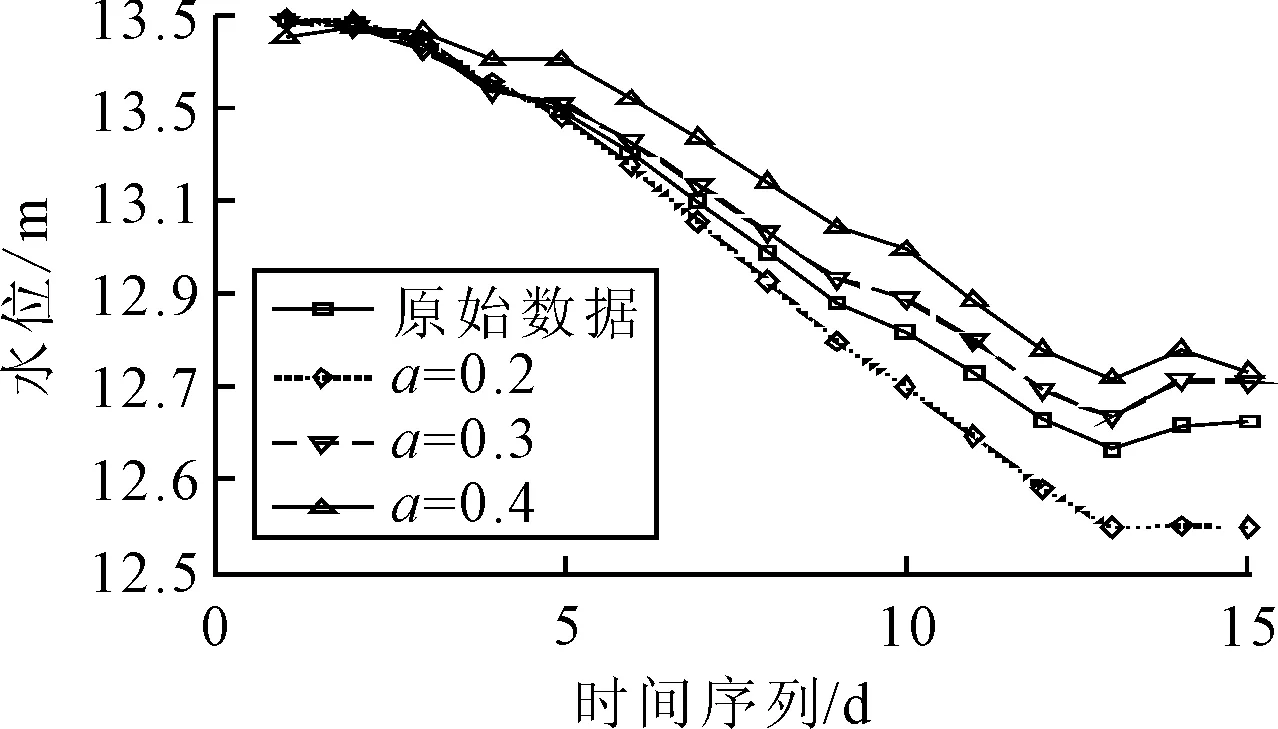
图2 平滑系数拟合曲线

2.2 估算初始值

初始值的估算对于指数平滑法最终结果具有较大影响.初始值的选取方法主要有两种，对于已有样本的平均及拟合[9].当样本数据量较大时，拟合方法更为精确，其具体过程如下.

对于缺失部分，首先获取其对应的历史数据，然后根据式(4)，对前三个已知数据进行拟合.此时，t= 0，将m= 1,2,3代入，用实际水位代替预测值，即

a0+b0+c0=y1

a0+2b0+4c0=y2

a0+3b0+9c0=y3

(8)

求解上述方程组得出a0，b0，c0，再将a0，b0，c0代入式(5)～(7)，结合数据特征选取适当的平滑系数α，解方程组即可得出初始值S0,1，S0,2，S0,3.

2.3 双向平滑法修正

由于时间序列特性，水位数据序列中任意数据前后数据均与该数据存有一定的相关关系.常用的单向预测方法可有效利用正向相关关系对数据进行预测，而反向关系经常被忽略.为充分利用已知数据，提高预测精度，由缺失部分之后的数据对丢失数据进行反向预测，并对双向预测结果进行加权求和.双向预测过程如下.

设有水位数据序列x={x1,x2,…,xn}，其中待修复数据点为xk，正向预测为以{x1,x2,…,xk-1}为预测数据集，由指数平滑公式得到正向预测结果yl，以{xn,xn-1,…,xk+1}为数据集，对待修复点进行反向预测，可得预测结果yr.

yr=ar+brm+crm2

(10)

yl=al+blm′+clm′2

(11)

对正反向预测结果进行加权求和，采用均值求和方式，最终预测结果表达为

(12)

3 案例分析

3.1 验数据采集

为验证基于双向指数平滑法的水位数据修复方法的有效性，以长江安庆段2016年7—8月水位数据为样本进行验证.其中水位数据为每日上午8时的实测水位，见图3.

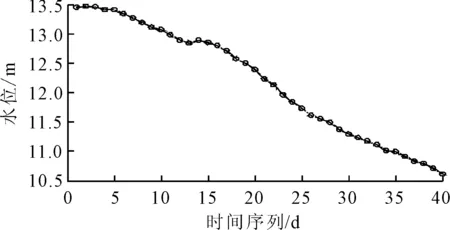
图3 安庆水位示意图(2016年7-8月)

3.2 双向预测修复

以前15个水位数据为已知数据，假设之后的一段数据为水位数据的连续缺失段.同时通过二次曲线拟合法得到三次指数平滑法的初始值分别为S0,1=12.995 0，S0,2=12.416 7，S0,3=11.675.反向预测的平滑系数选择方法类似，此处不再赘述.在MATLAB平台上，采用三次指数平滑法的双向预测模型，取正反双向预测值的平均值作为修正，对不同长度的缺失段数据进行验证.实验结果见图4～7.

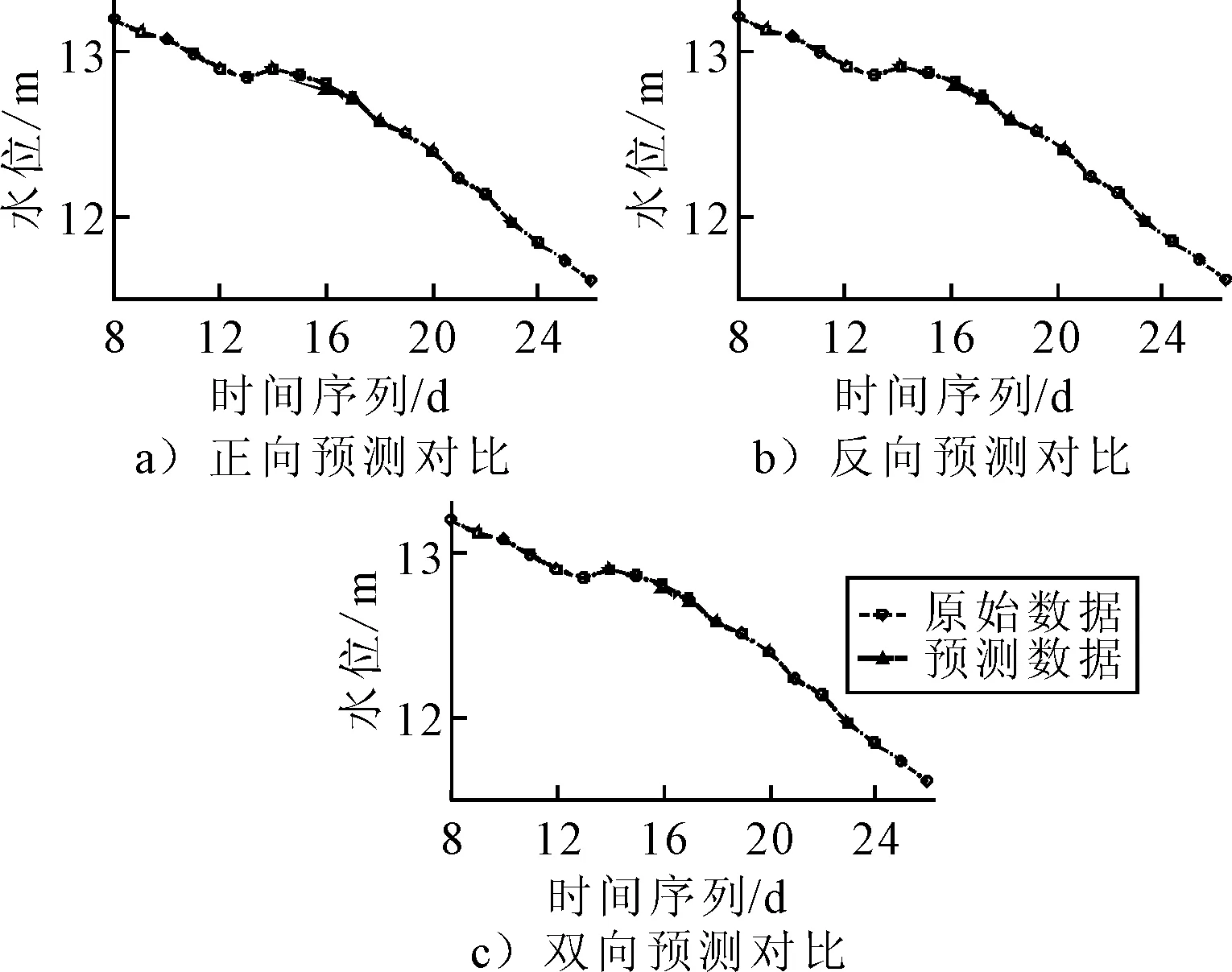
图4 缺失2个点时修复结果

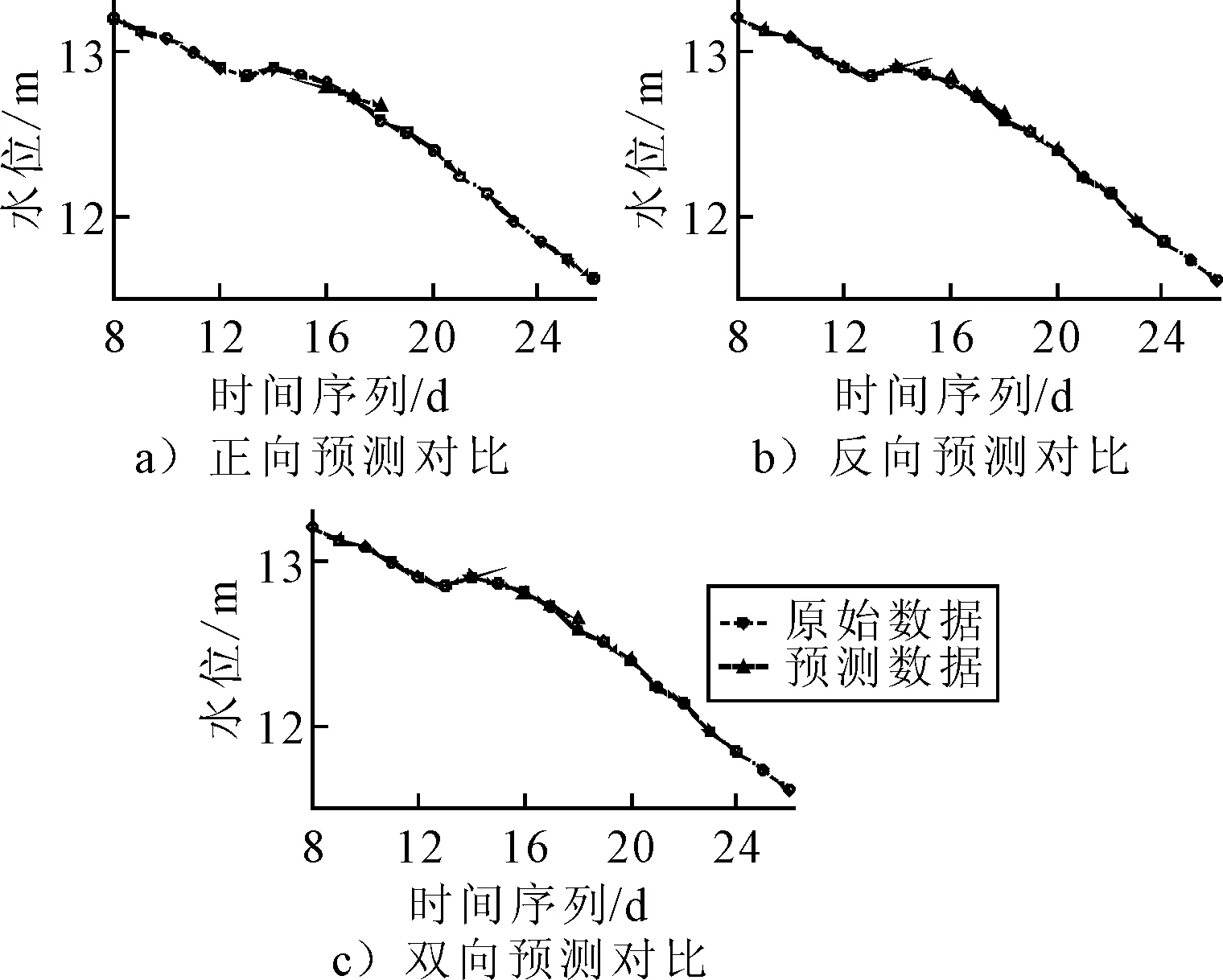
图5 缺失3个点时修复结果

图6 缺失4个点时修复结果

为验证实验结果，引入均方根误差(RMSE)、平均百分比误差(MAPE)以及模型决定系数(R2)对实验结果进行评价，其中均方根误差表示模型输出的平均误差，百分比误差表示输出的百分比误差，决定系数代表模型的拟合好坏程度，其值越高，模型的拟合程度越好.

评价指标具体公式为

(13)

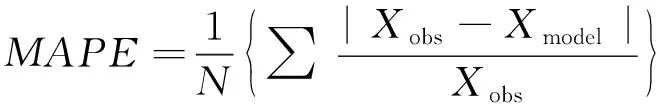
(14)

式中：Xobs为原始水位数据；Xmodel为模型预测数据.以下分别以连续缺失三个数据和五个数据为例，取安庆段和南京段足量水位数据进行双向修复实验，其结果由三类评价指标进行评价，见表2.

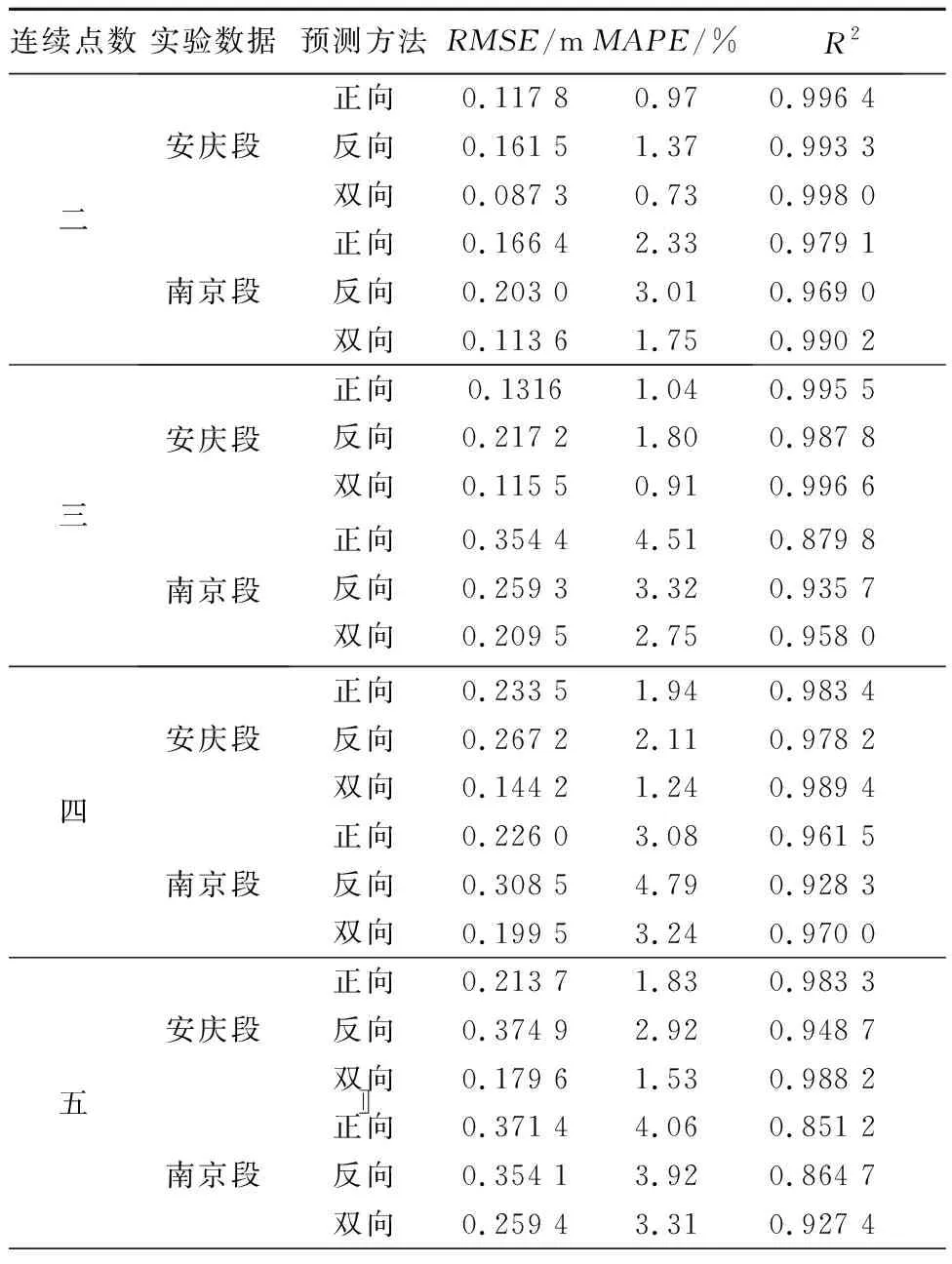
表2 修复结果

由表2可知，基于双向平滑指数的水位数据修复方法，在修复精度上，比正向及反向的单向方法均有提升；随着连续修复点数的增加，精度提升的数值逐渐增大.在修复点数为3时，均方跟误差约减少0.05 m，百分比误差降低0.5%.在修复点数增加至5时，均方跟误差降低约0.1米，百分比误差降低约1%，在模型拟合精度上均有所提升.